3.1用树状图或表格求概率(第3课时)-北师大版九年级数学上册同步练习(Word版)
文档属性
| 名称 | 3.1用树状图或表格求概率(第3课时)-北师大版九年级数学上册同步练习(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 147.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 13:57:47 | ||
图片预览



文档简介
北师大版数学九年级上册第三章第1节用树状图或表格求概率(第3课时)
一.选择题(共10小题)
1.从一个装有2个红球、3个白球的盒子里(球除颜色外其他都相同),先摸出一个球,不再放回,再摸出一个球,恰好摸到一个红球、一个白球的概率是( )
A.
B.
C.
D.
2.小甬与小真的学校组织优秀毕业生参加宁海中学自主招生考试,安排了三辆不同的车,小甬与小真都可以从三辆车中任选一辆搭乘,则小甬与小真搭乘同一辆车的概率为( )
A.
B.
C.
D.
3.用三种不同的颜色,将如图所示的四个区域涂色,每种颜色至少用1次,则相邻的区域不涂同一种颜色的概率为( )
A.
B.
C.
D.
4.众所周知,“石头、剪刀、布”游戏规则是比赛时双方任意出“石头”、“剪刀”、“布”这三种手势中的一种.石头胜剪刀,剪刀胜布,布胜石头,若双方出相同手势,则算打平.小明和小红玩这个游戏,他们随机出一种手势,则小明获胜的概率为( )
A.
B.
C.
D.
5.上蔡县是古蔡国所在地,有着悠久的历史,拥有很多重点古迹.某中学九年级历史爱好者小组成员小华和小玲两人计划在寒假期间从“蔡国故城、白圭庙、伏羲画卦亭”三个古迹景点随机选择其中一个去参观,两人恰好选择同一古迹景点的概率是( )
A.
B.
C.
D.
6.九年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率( )
A.
B.
C.
D.
7.某单行道路的路口,只能直行或右转,任意一辆车通过路口时直行或右转的概率相同.有3辆车通过路口.恰好有2辆车直行的概率是( )
A.
B.
C.
D.
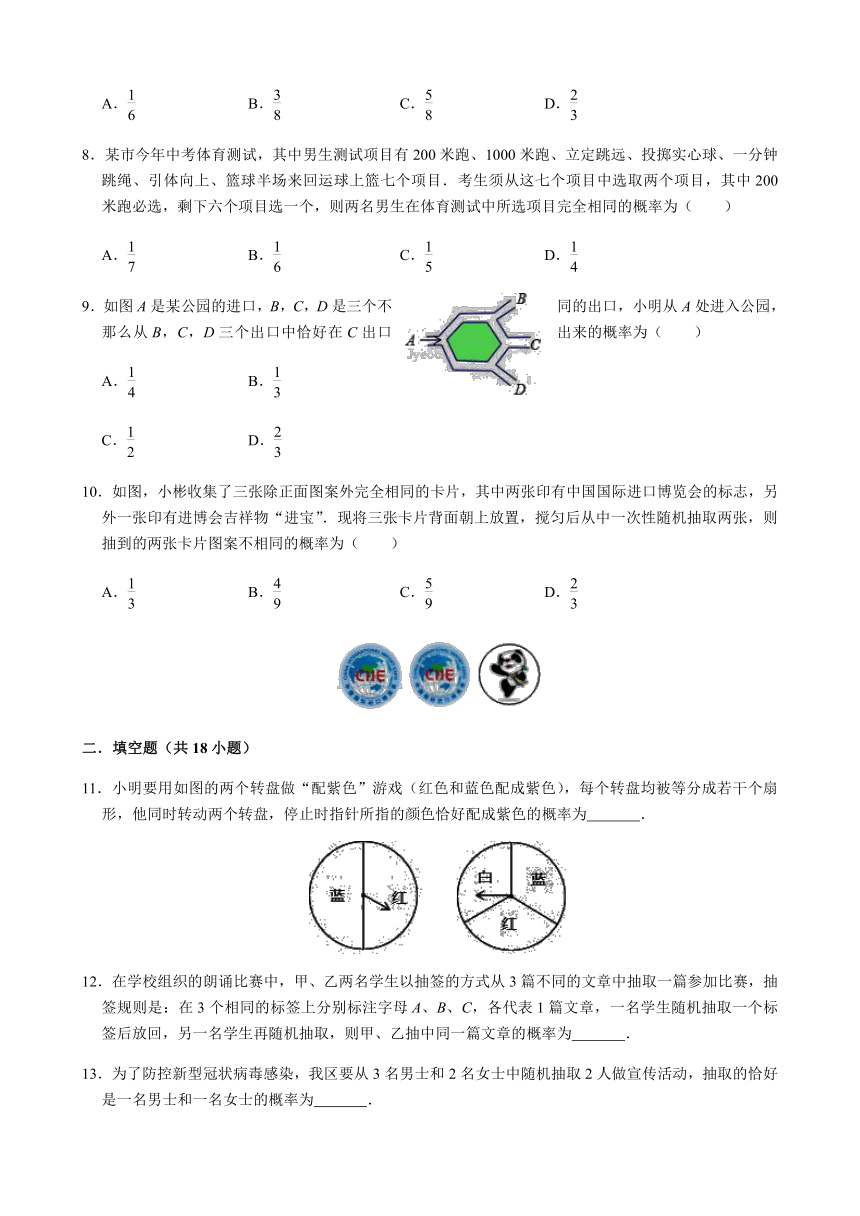
8.某市今年中考体育测试,其中男生测试项目有200米跑、1000米跑、立定跳远、投掷实心球、一分钟跳绳、引体向上、篮球半场来回运球上篮七个项目.考生须从这七个项目中选取两个项目,其中200米跑必选,剩下六个项目选一个,则两名男生在体育测试中所选项目完全相同的概率为( )
A.
B.
C.
D.
9.如图A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么从B,C,D三个出口中恰好在C出口出来的概率为( )
A.
B.
C.
D.
10.如图,小彬收集了三张除正面图案外完全相同的卡片,其中两张印有中国国际进口博览会的标志,另外一张印有进博会吉祥物“进宝”.现将三张卡片背面朝上放置,搅匀后从中一次性随机抽取两张,则抽到的两张卡片图案不相同的概率为( )
A.
B.
C.
D.
二.填空题(共18小题)
11.小明要用如图的两个转盘做“配紫色”游戏(红色和蓝色配成紫色),每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好配成紫色的概率为
.
12.在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取,则甲、乙抽中同一篇文章的概率为
.
13.为了防控新型冠状病毒感染,我区要从3名男士和2名女士中随机抽取2人做宣传活动,抽取的恰好是一名男士和一名女士的概率为
.
14.2019宁波国际马拉松竞赛在北仑梅山和春晓举行,项目共四项:A.全程马拉松,B.半程马拉松,C.10公里健康跑,D.4公里迷你跑.小明和小亮参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到四个项目组,则小明和小亮被分配到不同项目组的概率为
.
15.甲、乙两地共有A,B,C,D四路公交车往返,现在小明和小伟先后从甲地前往乙地(假设他们两人坐上A,B,C,D四路公交车的可能性是相同的),则他们乘坐同一路公交车的概率是
.
16.在一个不透明的袋子中装有红、白两种颜色的球(形状、大小、质地完全相同)共5个,其中白球有3个.每次从中随机摸出一个球,并记下颜色后放回,那么从袋子中连续摸出两次红球的概率是
.
三、解答题(本大题共5小题,共50分)
17.为阻断疫情向校园蔓延,确保师生生命安全和身体健康,教育部2020年1月29日下发通知,要求今年春季学期延期开学,“停课不停学”,统筹利用网络电视资源进行教学,某校为了让学生能够达到最佳的学习效果,确定老师们可以选用以下三种直播授课方式:A.晓黑板直播;
B.钉钉直播;
C.腾讯会议直播.
(1)王燕老师从三种网络授课方式中随机选取一种,是晓黑板直播的概率为
;
(2)王燕和陈明两位老师从中随机各选取一种网络直播方式进行授课,请你用列表法或画树状图法,求出王燕和陈明两位老师选取不同的网络直播授课方式的概率.
18.“吾悦广场”开展“有奖大酬宾”活动,凡在“吾悦广场”消费的顾客,均可凭消费小票参与转转盘抽奖活动.如图,是一个材质均匀可自由转动的转盘,转盘被等分成A、B、C、D、E五个扇形区域,依次写有:绿茶、欢迎惠顾、红茶、可乐和谢谢参与,如果转到区域为“可乐”、“绿茶”、“红茶”,则可领到对应的奖品.若转盘停止后,指针指向两区域的边界,顾客可以再转动转盘一次,直到指针不指向边界时停止.
根据以上规则,回答下列问题:
(1)小王同学转动转盘一次获得奖品的概率是
.
(2)小李同学有两次转转盘抽奖的机会,请你用列表或画树状图的方法,求小李同学获得“至少领到一瓶可乐”的概率.
19.王老师为了解所教班级学生自主学习、合作交流的能力情况,对所教学生进行了一个学年的跟踪调查,把调查结果分成四类:A(非常好)、B(良好)、C(一般)、D(较差).学年结束王老师将随机抽取部分学生的调查结果绘制成如图两幅不完整的统计图,请你根据已有信息解答下列问题:
(1)这次随机抽取的样本容量是
,其中C类女生有
名,D类男生有
名,扇形统计图中D类所对应的圆心角为
度;
(2)将条形统计图补充完整;
(3)现准备从被调查的A类和D类学生中分别选取一位同学进行“手拉手”学习,请用列表法或画树状图法求出所选两位同学恰好是一男一女的概率.
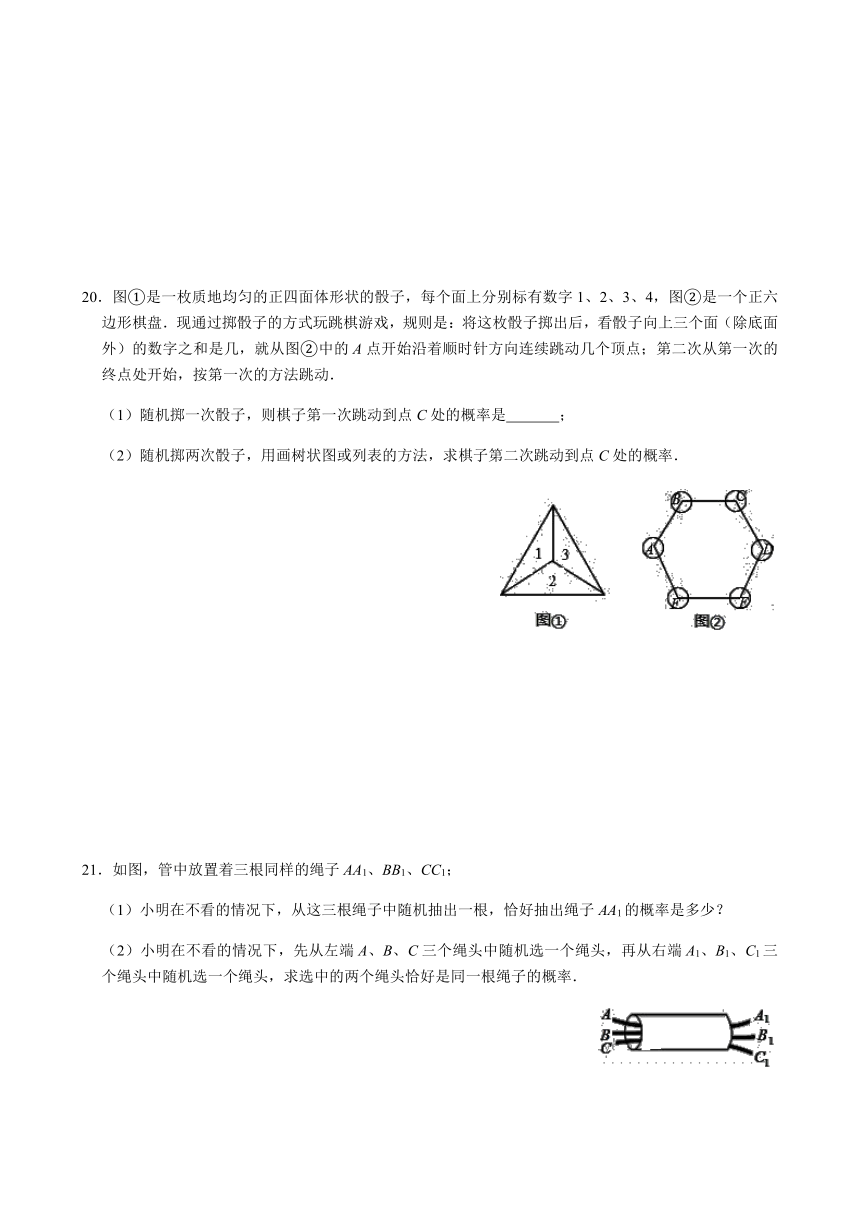
20.图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1、2、3、4,图②是一个正六边形棋盘.现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点;第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子第一次跳动到点C处的概率是
;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子第二次跳动到点C处的概率.
21.如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明在不看的情况下,从这三根绳子中随机抽出一根,恰好抽出绳子AA1的概率是多少?
(2)小明在不看的情况下,先从左端A、B、C三个绳头中随机选一个绳头,再从右端A1、B1、C1三个绳头中随机选一个绳头,求选中的两个绳头恰好是同一根绳子的概率.
22.图①是一个转盘,转盘被等分成三个区域,并分别标有数字2、3、7,图②是一个正五边形棋盘,现通过转动转盘的方式玩跳棋游戏.规则如下:将转盘转动后,看转盘指针指向的数字是几,就从图②中的A点开始在正五边形边上沿着顺时针方向连续跳过几个边(指针指向边界不计),第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机转动一次转盘,则棋子跳动到点C处的概率是
;
(2)随机转动两次转盘,用画树状图或列表的方法.求棋子最终跳动到点A处的概率.
答案
一、选择题
1.C
2.B
3.B
4.B
5.A
6.D
7.B
8.B
9.B
10.D
二、填空题
11.
12.
13.
14.
15.
16.
三、解答题
17.解:(1)∵确定老师们可以选用以下三种直播授课方式:A.晓黑板直播;
B.钉钉直播;
C.腾讯会议直播,∴王燕老师从三种网络授课方式中随机选取一种,是晓黑板直播的概率=.
(2)根据题意,列表格如下:
A
B
C
A
(A,A)
(A,B)
(A,C)
B
(B,A)
(B,B)
(B,C)
C
(C,A)
(C,B)
(C,C)
共有9种等可能性的结果,其中两位老师选取不同的网络直播授课方式的结果有6种,
所以,P(两位老师选取不同的网络直播授课方式)==.
18.解:(1)∵转盘被等分成A、B、C、D、E五个扇形区域,转到区域为“可乐”、“绿茶”、“红茶”,则可领到对应的奖品,
∴小王同学转动转盘一次获得奖品的概率是;
(2)根据题意画图如下:
共有25种等情况数,其中小李同学获得“至少领到一瓶可乐”的5种,
则小李同学获得“至少领到一瓶可乐”的概率是:=.
19.解:(1)这次随机抽取的样本容量是(1+2)÷15%=20,
C类女生有20×25%﹣3=2(名),D类男生有1名,
扇形统计图中D类所对应的圆心角为360°×=36°,
(2)补全图形如下:
(3)画树状图如下:
一共有6种等可能的结果:男男、男女、女男、女女、女男、女女,其中一男一女的情况有3种,
所以所选两位同学恰好是一男一女的概率为=.
20.解:(1)随机掷一次骰子,则棋子跳动到点C处的概率是,
(2)列表如下:
共有16种可能,和为14可以到达点C,有3种情形,
所以棋子第二次跳动到点C处的概率为.
21.解:(1)∵管中放置着三根同样的绳子AA1、BB1、CC1,
∴恰好选中绳子AA1的概率是;
(2)列表得:
A1
B1
C1
A
AA1
AB1
AC1
B
BA1
BB1
BC1
C
CA1
CB1
CC1
由表可知共有9种等可能结果,其中选中的两个绳头恰好是同一根绳子的有3种结果,
∴选中的两个绳头恰好是同一根绳子的概率为.
22.解:(1)随机转动一次转盘,则棋子跳动到点C处的概率=;
(2)画树状图为:
共有9种等可能的结果数,其中棋子最终跳动到点A处的结果数为4,
所以棋子最终跳动到点A处的概率=.
一.选择题(共10小题)
1.从一个装有2个红球、3个白球的盒子里(球除颜色外其他都相同),先摸出一个球,不再放回,再摸出一个球,恰好摸到一个红球、一个白球的概率是( )
A.
B.
C.
D.
2.小甬与小真的学校组织优秀毕业生参加宁海中学自主招生考试,安排了三辆不同的车,小甬与小真都可以从三辆车中任选一辆搭乘,则小甬与小真搭乘同一辆车的概率为( )
A.
B.
C.
D.
3.用三种不同的颜色,将如图所示的四个区域涂色,每种颜色至少用1次,则相邻的区域不涂同一种颜色的概率为( )
A.
B.
C.
D.
4.众所周知,“石头、剪刀、布”游戏规则是比赛时双方任意出“石头”、“剪刀”、“布”这三种手势中的一种.石头胜剪刀,剪刀胜布,布胜石头,若双方出相同手势,则算打平.小明和小红玩这个游戏,他们随机出一种手势,则小明获胜的概率为( )
A.
B.
C.
D.
5.上蔡县是古蔡国所在地,有着悠久的历史,拥有很多重点古迹.某中学九年级历史爱好者小组成员小华和小玲两人计划在寒假期间从“蔡国故城、白圭庙、伏羲画卦亭”三个古迹景点随机选择其中一个去参观,两人恰好选择同一古迹景点的概率是( )
A.
B.
C.
D.
6.九年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率( )
A.
B.
C.
D.
7.某单行道路的路口,只能直行或右转,任意一辆车通过路口时直行或右转的概率相同.有3辆车通过路口.恰好有2辆车直行的概率是( )
A.
B.
C.
D.
8.某市今年中考体育测试,其中男生测试项目有200米跑、1000米跑、立定跳远、投掷实心球、一分钟跳绳、引体向上、篮球半场来回运球上篮七个项目.考生须从这七个项目中选取两个项目,其中200米跑必选,剩下六个项目选一个,则两名男生在体育测试中所选项目完全相同的概率为( )
A.
B.
C.
D.
9.如图A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么从B,C,D三个出口中恰好在C出口出来的概率为( )
A.
B.
C.
D.
10.如图,小彬收集了三张除正面图案外完全相同的卡片,其中两张印有中国国际进口博览会的标志,另外一张印有进博会吉祥物“进宝”.现将三张卡片背面朝上放置,搅匀后从中一次性随机抽取两张,则抽到的两张卡片图案不相同的概率为( )
A.
B.
C.
D.
二.填空题(共18小题)
11.小明要用如图的两个转盘做“配紫色”游戏(红色和蓝色配成紫色),每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好配成紫色的概率为
.
12.在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取,则甲、乙抽中同一篇文章的概率为
.
13.为了防控新型冠状病毒感染,我区要从3名男士和2名女士中随机抽取2人做宣传活动,抽取的恰好是一名男士和一名女士的概率为
.
14.2019宁波国际马拉松竞赛在北仑梅山和春晓举行,项目共四项:A.全程马拉松,B.半程马拉松,C.10公里健康跑,D.4公里迷你跑.小明和小亮参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到四个项目组,则小明和小亮被分配到不同项目组的概率为
.
15.甲、乙两地共有A,B,C,D四路公交车往返,现在小明和小伟先后从甲地前往乙地(假设他们两人坐上A,B,C,D四路公交车的可能性是相同的),则他们乘坐同一路公交车的概率是
.
16.在一个不透明的袋子中装有红、白两种颜色的球(形状、大小、质地完全相同)共5个,其中白球有3个.每次从中随机摸出一个球,并记下颜色后放回,那么从袋子中连续摸出两次红球的概率是
.
三、解答题(本大题共5小题,共50分)
17.为阻断疫情向校园蔓延,确保师生生命安全和身体健康,教育部2020年1月29日下发通知,要求今年春季学期延期开学,“停课不停学”,统筹利用网络电视资源进行教学,某校为了让学生能够达到最佳的学习效果,确定老师们可以选用以下三种直播授课方式:A.晓黑板直播;
B.钉钉直播;
C.腾讯会议直播.
(1)王燕老师从三种网络授课方式中随机选取一种,是晓黑板直播的概率为
;
(2)王燕和陈明两位老师从中随机各选取一种网络直播方式进行授课,请你用列表法或画树状图法,求出王燕和陈明两位老师选取不同的网络直播授课方式的概率.
18.“吾悦广场”开展“有奖大酬宾”活动,凡在“吾悦广场”消费的顾客,均可凭消费小票参与转转盘抽奖活动.如图,是一个材质均匀可自由转动的转盘,转盘被等分成A、B、C、D、E五个扇形区域,依次写有:绿茶、欢迎惠顾、红茶、可乐和谢谢参与,如果转到区域为“可乐”、“绿茶”、“红茶”,则可领到对应的奖品.若转盘停止后,指针指向两区域的边界,顾客可以再转动转盘一次,直到指针不指向边界时停止.
根据以上规则,回答下列问题:
(1)小王同学转动转盘一次获得奖品的概率是
.
(2)小李同学有两次转转盘抽奖的机会,请你用列表或画树状图的方法,求小李同学获得“至少领到一瓶可乐”的概率.
19.王老师为了解所教班级学生自主学习、合作交流的能力情况,对所教学生进行了一个学年的跟踪调查,把调查结果分成四类:A(非常好)、B(良好)、C(一般)、D(较差).学年结束王老师将随机抽取部分学生的调查结果绘制成如图两幅不完整的统计图,请你根据已有信息解答下列问题:
(1)这次随机抽取的样本容量是
,其中C类女生有
名,D类男生有
名,扇形统计图中D类所对应的圆心角为
度;
(2)将条形统计图补充完整;
(3)现准备从被调查的A类和D类学生中分别选取一位同学进行“手拉手”学习,请用列表法或画树状图法求出所选两位同学恰好是一男一女的概率.
20.图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1、2、3、4,图②是一个正六边形棋盘.现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点;第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子第一次跳动到点C处的概率是
;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子第二次跳动到点C处的概率.
21.如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明在不看的情况下,从这三根绳子中随机抽出一根,恰好抽出绳子AA1的概率是多少?
(2)小明在不看的情况下,先从左端A、B、C三个绳头中随机选一个绳头,再从右端A1、B1、C1三个绳头中随机选一个绳头,求选中的两个绳头恰好是同一根绳子的概率.
22.图①是一个转盘,转盘被等分成三个区域,并分别标有数字2、3、7,图②是一个正五边形棋盘,现通过转动转盘的方式玩跳棋游戏.规则如下:将转盘转动后,看转盘指针指向的数字是几,就从图②中的A点开始在正五边形边上沿着顺时针方向连续跳过几个边(指针指向边界不计),第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机转动一次转盘,则棋子跳动到点C处的概率是
;
(2)随机转动两次转盘,用画树状图或列表的方法.求棋子最终跳动到点A处的概率.
答案
一、选择题
1.C
2.B
3.B
4.B
5.A
6.D
7.B
8.B
9.B
10.D
二、填空题
11.
12.
13.
14.
15.
16.
三、解答题
17.解:(1)∵确定老师们可以选用以下三种直播授课方式:A.晓黑板直播;
B.钉钉直播;
C.腾讯会议直播,∴王燕老师从三种网络授课方式中随机选取一种,是晓黑板直播的概率=.
(2)根据题意,列表格如下:
A
B
C
A
(A,A)
(A,B)
(A,C)
B
(B,A)
(B,B)
(B,C)
C
(C,A)
(C,B)
(C,C)
共有9种等可能性的结果,其中两位老师选取不同的网络直播授课方式的结果有6种,
所以,P(两位老师选取不同的网络直播授课方式)==.
18.解:(1)∵转盘被等分成A、B、C、D、E五个扇形区域,转到区域为“可乐”、“绿茶”、“红茶”,则可领到对应的奖品,
∴小王同学转动转盘一次获得奖品的概率是;
(2)根据题意画图如下:
共有25种等情况数,其中小李同学获得“至少领到一瓶可乐”的5种,
则小李同学获得“至少领到一瓶可乐”的概率是:=.
19.解:(1)这次随机抽取的样本容量是(1+2)÷15%=20,
C类女生有20×25%﹣3=2(名),D类男生有1名,
扇形统计图中D类所对应的圆心角为360°×=36°,
(2)补全图形如下:
(3)画树状图如下:
一共有6种等可能的结果:男男、男女、女男、女女、女男、女女,其中一男一女的情况有3种,
所以所选两位同学恰好是一男一女的概率为=.
20.解:(1)随机掷一次骰子,则棋子跳动到点C处的概率是,
(2)列表如下:
共有16种可能,和为14可以到达点C,有3种情形,
所以棋子第二次跳动到点C处的概率为.
21.解:(1)∵管中放置着三根同样的绳子AA1、BB1、CC1,
∴恰好选中绳子AA1的概率是;
(2)列表得:
A1
B1
C1
A
AA1
AB1
AC1
B
BA1
BB1
BC1
C
CA1
CB1
CC1
由表可知共有9种等可能结果,其中选中的两个绳头恰好是同一根绳子的有3种结果,
∴选中的两个绳头恰好是同一根绳子的概率为.
22.解:(1)随机转动一次转盘,则棋子跳动到点C处的概率=;
(2)画树状图为:
共有9种等可能的结果数,其中棋子最终跳动到点A处的结果数为4,
所以棋子最终跳动到点A处的概率=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
