22.2.5一元二次方程的根与系数关系-华东师大版九年级数学上册课件(共16张PPT)
文档属性
| 名称 | 22.2.5一元二次方程的根与系数关系-华东师大版九年级数学上册课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 14:09:29 | ||
图片预览




文档简介
(共16张PPT)
§22.2一元二次方程的解法
——根与系数的关系
知识回顾
1.一元二次方程的一般形式是什么?
2、一元二次方程的求根公式?
(
)
一元二次方程的一般形式是:
根与系数关系探索
方程
-3
-4
2
-3
5
4
1
-4
3
-1
4
1
1、上面三个方程的二次项系数有何特点?
想一想
2、
和
与方程各项系数有什么关系?
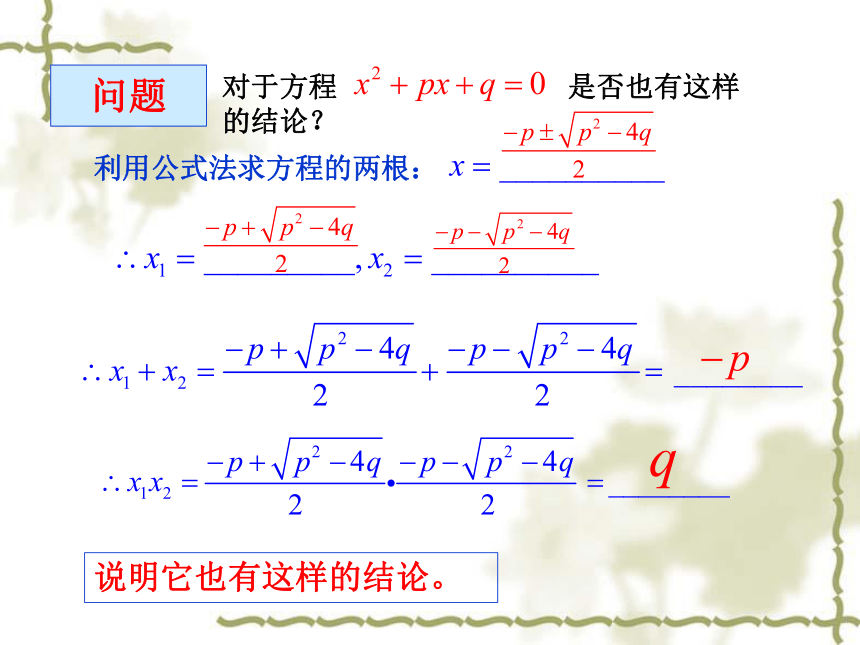
问题
对于方程
是否也有这样的结论?
利用公式法求方程的两根:
说明它也有这样的结论。
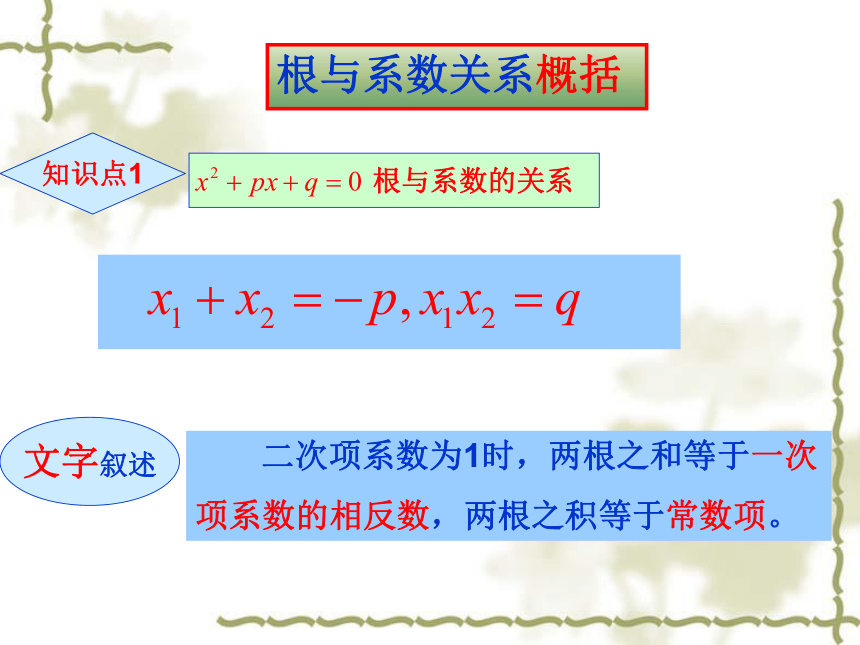
根与系数关系概括
知识点1
根与系数的关系
文字叙述
二次项系数为1时,两根之和等于一次
项系数的相反数,两根之积等于常数项。
问题
针对这个方程,你能求出两根的和与积吗?
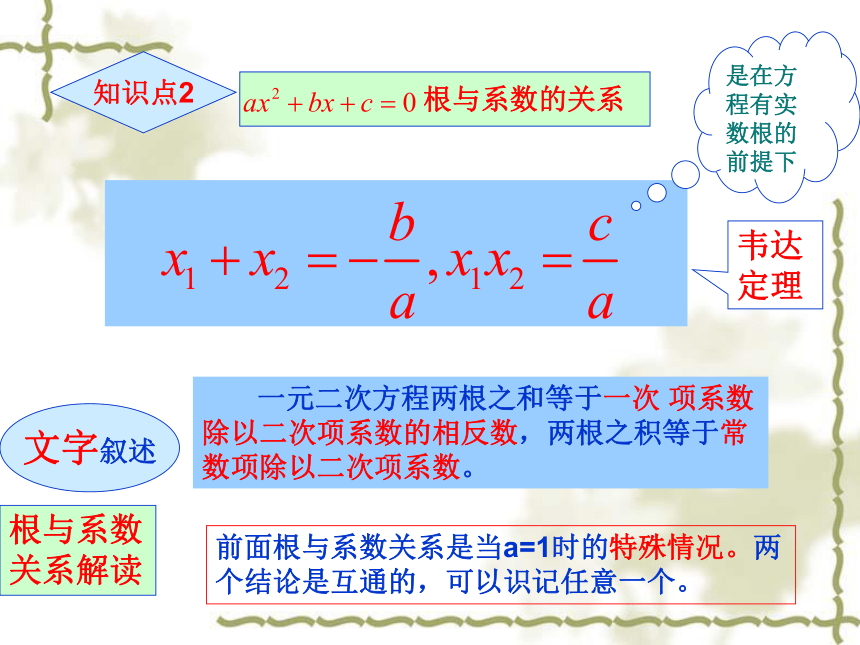
知识点2
根与系数的关系
文字叙述
一元二次方程两根之和等于一次
项系数除以二次项系数的相反数,两根之积等于常数项除以二次项系数。
是在方程有实数根的前提下
韦达定理
根与系数关系解读
前面根与系数关系是当a=1时的特殊情况。两个结论是互通的,可以识记任意一个。
根与系数关系应用
知识点3
1.直接运用
根与系数的关系
例1
(1)、已知
是方程
的两根,则
-1
(2)、已知
是方程
的两根,则
2.求关于两根的对称式的值
例2
已知方程
的两实数根分别为
不解方程求下列各式的值:
思路:
关键是将代数式用两根和与积表示出来
【解】
由根与系数的关系,可得
-3
-1
=11
=3
=2
求对称式的值的关键是:将对称式用两根之和与
两根之积正确表示出来。
学法
指导
几种常见对称式的变形
对应练习
1、已知关于x的一元二次方程
的两个实数根分别为
则
9
点拨:
2、设
是方程
的两个实数根,则
的值为(
)
点拨:
B
知识点3
求一元二次方程待定的系数
例3
已知关于x的一元二次方程
的一
个根为2,则另一个根和k的值分别为(
)
A.-2,0
B.1,4
C.2,-4
D.4,0
点拨:
设方程的另一个根为
由于方程的常数项没含k,所以选两根之积可求出另一个根
即
又因为k是在一次项系数中,所以,再用两根之和便可求
出k的值。
即
A
对应练习
(课本P35练习)
解下列各题:(1)已知关于x的方程
的两个根是1和-3
,求m和n
的值。
(2)已知关于x的方程
的一个根是-4,求它的另一个根和m的值。
课堂小结
这节课我们收获了:
1、在方程
中,根与系数的关系:
2、在二次项系数为1的特殊方程
中,根与系数的关系:
3、一元二次方程根与系数的关系有哪些常见的应用?你掌握了吗?
(1)直接运用
(2)求对称式的值
(3)求一元二次方程中待定系数
中考对接
1、已知一元二次方程
有一个根为2,则另一个根为(
)
A.2
B.3
C.4
D.8
C
2、若
是关于x的方程
的一个根,则此方程的
另一个根是
5
课堂作业:
P.36
10.
11
§22.2一元二次方程的解法
——根与系数的关系
知识回顾
1.一元二次方程的一般形式是什么?
2、一元二次方程的求根公式?
(
)
一元二次方程的一般形式是:
根与系数关系探索
方程
-3
-4
2
-3
5
4
1
-4
3
-1
4
1
1、上面三个方程的二次项系数有何特点?
想一想
2、
和
与方程各项系数有什么关系?
问题
对于方程
是否也有这样的结论?
利用公式法求方程的两根:
说明它也有这样的结论。
根与系数关系概括
知识点1
根与系数的关系
文字叙述
二次项系数为1时,两根之和等于一次
项系数的相反数,两根之积等于常数项。
问题
针对这个方程,你能求出两根的和与积吗?
知识点2
根与系数的关系
文字叙述
一元二次方程两根之和等于一次
项系数除以二次项系数的相反数,两根之积等于常数项除以二次项系数。
是在方程有实数根的前提下
韦达定理
根与系数关系解读
前面根与系数关系是当a=1时的特殊情况。两个结论是互通的,可以识记任意一个。
根与系数关系应用
知识点3
1.直接运用
根与系数的关系
例1
(1)、已知
是方程
的两根,则
-1
(2)、已知
是方程
的两根,则
2.求关于两根的对称式的值
例2
已知方程
的两实数根分别为
不解方程求下列各式的值:
思路:
关键是将代数式用两根和与积表示出来
【解】
由根与系数的关系,可得
-3
-1
=11
=3
=2
求对称式的值的关键是:将对称式用两根之和与
两根之积正确表示出来。
学法
指导
几种常见对称式的变形
对应练习
1、已知关于x的一元二次方程
的两个实数根分别为
则
9
点拨:
2、设
是方程
的两个实数根,则
的值为(
)
点拨:
B
知识点3
求一元二次方程待定的系数
例3
已知关于x的一元二次方程
的一
个根为2,则另一个根和k的值分别为(
)
A.-2,0
B.1,4
C.2,-4
D.4,0
点拨:
设方程的另一个根为
由于方程的常数项没含k,所以选两根之积可求出另一个根
即
又因为k是在一次项系数中,所以,再用两根之和便可求
出k的值。
即
A
对应练习
(课本P35练习)
解下列各题:(1)已知关于x的方程
的两个根是1和-3
,求m和n
的值。
(2)已知关于x的方程
的一个根是-4,求它的另一个根和m的值。
课堂小结
这节课我们收获了:
1、在方程
中,根与系数的关系:
2、在二次项系数为1的特殊方程
中,根与系数的关系:
3、一元二次方程根与系数的关系有哪些常见的应用?你掌握了吗?
(1)直接运用
(2)求对称式的值
(3)求一元二次方程中待定系数
中考对接
1、已知一元二次方程
有一个根为2,则另一个根为(
)
A.2
B.3
C.4
D.8
C
2、若
是关于x的方程
的一个根,则此方程的
另一个根是
5
课堂作业:
P.36
10.
11
