22.3实践与探索(利润问题)-华东师大版九年级数学上册课件(共14张PPT)
文档属性
| 名称 | 22.3实践与探索(利润问题)-华东师大版九年级数学上册课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 921.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 14:10:39 | ||
图片预览






文档简介
(共14张PPT)
§22.3实践与探索
---------利润问题
1.一件衣服进价为m元,售价为n元,这件衣服的利润是(
)元。
n-m
2.某玩具售出一件获利30元,现在降价3元销售,售出10件可获利(
)元.
270
利润=售价-进价
单件利润×销售总量=总利润
(30-3)×10=270
知识回顾
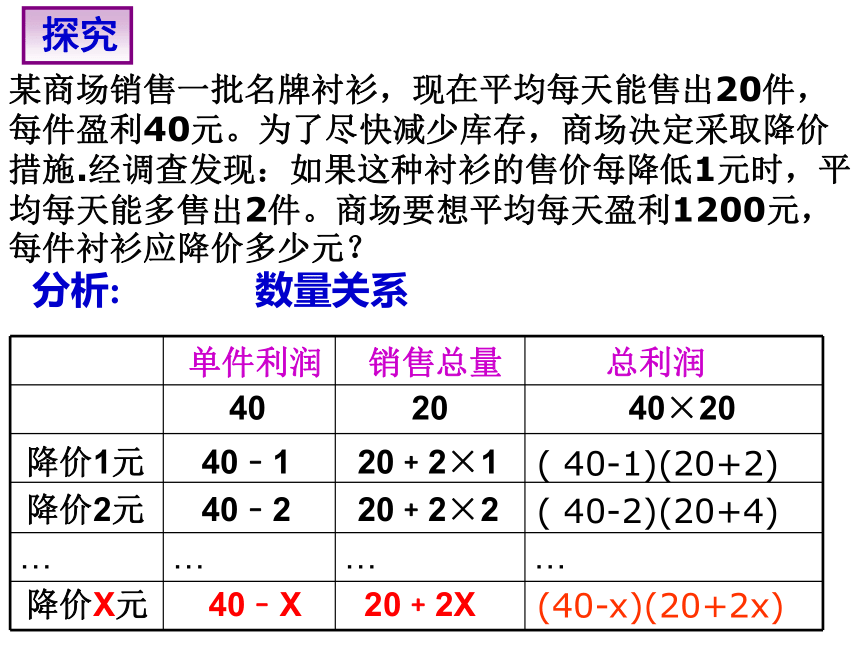
某商场销售一批名牌衬衫,现在平均每天能售出20件,每件盈利40元。为了尽快减少库存,商场决定采取降价措施.经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件。商场要想平均每天盈利1200元,每件衬衫应降价多少元?
分析:
数量关系
…
…
…
…
单件利润
销售总量
总利润
40
20
40×20
降价1元
降价2元
降价X元
40﹣1
40﹣2
40﹣X
20﹢2×1
20﹢2×2
20﹢2X
(
40-1)(20+2)
(
40-2)(20+4)
(40-x)(20+2x)
探究
解:
设每件衬衫降价x元.根据题意,得:
(20+2x)(40-x)=1200
整理得:x2-30x+200=0
解这个方程,得:x1=10,x2=20
因为要尽快减少库存,降价越多,销售越快,所以每件应降价20元。
答:每件衬衫应降价20元。
拓展探究
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.经调查发现,
如果这种衬衫的售价每降价1元,商场平均每天可多售出2件.
(1)如果商场通过销售这批衬衫每天要盈利1300元,可能吗?说明理由。
(2)商场能获得的最大利润是多少?
整理得:x2-30x+250=0
∵△=
∴商场不可能每天盈利1300元.
解:(1)每天要盈利1300元商场不可能每天盈利1300元,理由如下:
(40﹣x)(20+2x)=1300,
∴x=15时,W最大=1250元.
∴商场能获得的最大利润是1250元.
(2)设商场每天的盈利为W元,由题意,得
W=(40﹣x)(20+2x),
W=﹣2(x﹣15)2+1250
∴a=﹣2<0,
1.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.市场调研表明:当销售价为每上涨1元时,其销售量就将减少10个.商场要想销售利润平均每月达到10000元,每个台灯应涨价多少元?
解:
设每个台灯涨价x元,根据题意,得:
(40+x-30)(600-10x)=10000
整理得:x2-50x+400=0
解这个方程,得:x1=10,x2=40
答:每个台灯应涨价10元或40元。
如果添上“商场想尽可能减少进货成本”,结果会发生什么变化?
随堂练习
2.
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
(x﹣8)(200﹣
×10)=640,
原价为10元,则定价为12元和16元都符合题意(加价减销),
解:设售价为x元,根据题意列方程得
整理得:(x﹣8)(400﹣20x)=640,
即x2﹣28x+192=0,
答:将每件售价定为12或16元时,才能使每天利润为640元.
解得x1=12,x2=16.
1.通过本节课的学习,你有什么收获?
2.在解题过程中需要注意什么?
小结
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?题中包含哪些等量关系?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:”答”也必需是完整的语句,注明单位.
列方程解应用题的关键是:
找出等量关系.
课堂作业:
P.42
练习
2
P.43
习题22.3
5
课外作业
某商场购进一批单价为16元的日用品,销售一段时间后,为获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.每月销售件数y(件)与价格x(元/件)满足关系式y=kx+b.
(1)确定k与b的值,并指出x的取值范围.
(2)为使每月获利1920元,问:商品应定为每件多少元?
(3)为使每月获得最大利润,问:商品应定为每件多少元?
§22.3实践与探索
---------利润问题
1.一件衣服进价为m元,售价为n元,这件衣服的利润是(
)元。
n-m
2.某玩具售出一件获利30元,现在降价3元销售,售出10件可获利(
)元.
270
利润=售价-进价
单件利润×销售总量=总利润
(30-3)×10=270
知识回顾
某商场销售一批名牌衬衫,现在平均每天能售出20件,每件盈利40元。为了尽快减少库存,商场决定采取降价措施.经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件。商场要想平均每天盈利1200元,每件衬衫应降价多少元?
分析:
数量关系
…
…
…
…
单件利润
销售总量
总利润
40
20
40×20
降价1元
降价2元
降价X元
40﹣1
40﹣2
40﹣X
20﹢2×1
20﹢2×2
20﹢2X
(
40-1)(20+2)
(
40-2)(20+4)
(40-x)(20+2x)
探究
解:
设每件衬衫降价x元.根据题意,得:
(20+2x)(40-x)=1200
整理得:x2-30x+200=0
解这个方程,得:x1=10,x2=20
因为要尽快减少库存,降价越多,销售越快,所以每件应降价20元。
答:每件衬衫应降价20元。
拓展探究
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.经调查发现,
如果这种衬衫的售价每降价1元,商场平均每天可多售出2件.
(1)如果商场通过销售这批衬衫每天要盈利1300元,可能吗?说明理由。
(2)商场能获得的最大利润是多少?
整理得:x2-30x+250=0
∵△=
∴商场不可能每天盈利1300元.
解:(1)每天要盈利1300元商场不可能每天盈利1300元,理由如下:
(40﹣x)(20+2x)=1300,
∴x=15时,W最大=1250元.
∴商场能获得的最大利润是1250元.
(2)设商场每天的盈利为W元,由题意,得
W=(40﹣x)(20+2x),
W=﹣2(x﹣15)2+1250
∴a=﹣2<0,
1.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.市场调研表明:当销售价为每上涨1元时,其销售量就将减少10个.商场要想销售利润平均每月达到10000元,每个台灯应涨价多少元?
解:
设每个台灯涨价x元,根据题意,得:
(40+x-30)(600-10x)=10000
整理得:x2-50x+400=0
解这个方程,得:x1=10,x2=40
答:每个台灯应涨价10元或40元。
如果添上“商场想尽可能减少进货成本”,结果会发生什么变化?
随堂练习
2.
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
(x﹣8)(200﹣
×10)=640,
原价为10元,则定价为12元和16元都符合题意(加价减销),
解:设售价为x元,根据题意列方程得
整理得:(x﹣8)(400﹣20x)=640,
即x2﹣28x+192=0,
答:将每件售价定为12或16元时,才能使每天利润为640元.
解得x1=12,x2=16.
1.通过本节课的学习,你有什么收获?
2.在解题过程中需要注意什么?
小结
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?题中包含哪些等量关系?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:”答”也必需是完整的语句,注明单位.
列方程解应用题的关键是:
找出等量关系.
课堂作业:
P.42
练习
2
P.43
习题22.3
5
课外作业
某商场购进一批单价为16元的日用品,销售一段时间后,为获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.每月销售件数y(件)与价格x(元/件)满足关系式y=kx+b.
(1)确定k与b的值,并指出x的取值范围.
(2)为使每月获利1920元,问:商品应定为每件多少元?
(3)为使每月获得最大利润,问:商品应定为每件多少元?
