1.3.1 有理数的加法 第1课时 课件(共29张PPT)
文档属性
| 名称 | 1.3.1 有理数的加法 第1课时 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 22:15:12 | ||
图片预览








文档简介
(共29张PPT)
人教版
七上
1.3.1有理数的加法
第1课时
探究新知
教学重、难点
1.重点:掌握有理数的加法法则,能运用法则进行加法运算.
2.难点:探究异号两数相加的法则.
复习回顾
1.如果向东走5米记作+5米,那么向西走8米记作_____.
2.比较下列各数的大小:
3_____2
3____-2
-3_____2
-3____-2
3.已知a=-8,b=-3
则|a|+|b|=
,
则|a|─|b|=
.
>
>
<
<
-8米
11
5
探究新知
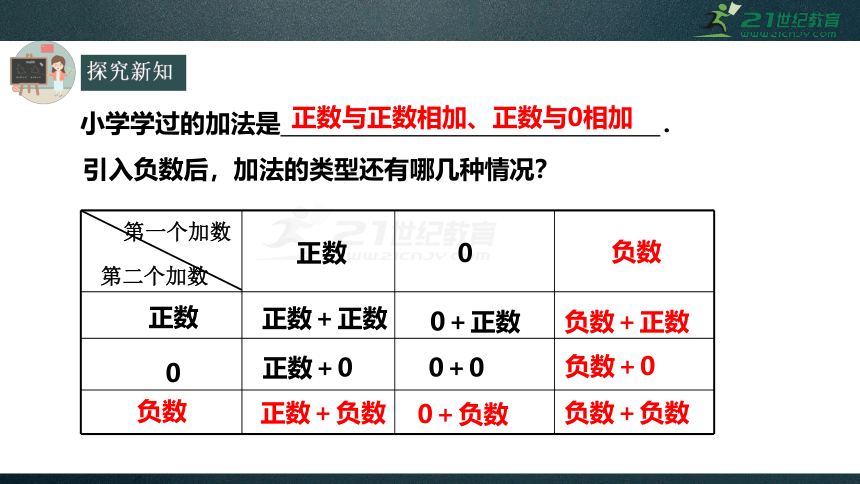
小学学过的加法是
.
正数与正数相加、正数与0相加
第二个加数
第一个加数
正数
0
正数
0
正数+正数
0+正数
0+0
正数+0
引入负数后,加法的类型还有哪几种情况?
负数
负数
正数+负数
0+负数
负数+正数
负数+0
负数+负数
探究新知
2.异号两数相加.
1.同号两数相加.
3.一个数与0相加.
思考:
在上述表格中,有理数加法我们可以化归为几个类型?
探究新知
小红向左右方向运动,我们规定向左为负,向右为正.向右运动5
m记作+5
m,向左运动5
m记作─5
m.
(1)如果小红先向右运动5
m,再向右运动3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
两次运动后,小红向右运动
米用算式来表示:
5
3
(+5)+(+3)=+8米
8
8
1.同号两数相加.
探究新知
(2)如果小红先向左运动5
m,再向左运动3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
两次运动后,小红向左运动
米用算式来表示:
(-5)+(-3)=-8
8
5
3
8
探究新知
(+5)+(+3)=+8
(-5)+(-3)=-8
思考:符号相同的两个数应如何相加呢?有什么发现?
加数符号“+”
加数符号“+”
和的符号“+”
加数符号“-”
加数符号“-”
和的符号“-”
加法法则一:
符号相同的两个数相加,结果的符号不变,绝对值相加.
归纳:
练一练
计算:
1.(+3)+(+7)
2.(-1)+(-3)
3.
-5.8+(-7.2)
探究新知
两次运动后,小红一共向右运动2米用算式来表示:
3
5
2
(3)如果小红先向左运动3
m,再向右运动5
m,那么两次运动的最后结果怎样?如何用算式表示?
(-3)+5=+(5-3)=+2
探究新知
两次运动后,小红一共向左运动2米用算式来表示:
5
3
2
(4)如果小红先向右运动3
m,再向左运动5
m,那么两次运动的最后结果怎样?如何用算式表示?
+3+(-5)
=-(5-3)=-2
探究新知
(-3)+(+5)=+(5-3)
思考:符号相同的两个数应如何相加呢?有什么发现?
加数符号“+”
加数符号“-”
和的符号取绝对值较大的加数的符号相同“+”
并用较大的绝对值减去较小的绝对值
(+3)+(-5)=-(5-3)
加数符号“-”
加数符号“+”
和的符号取绝对值较大的加数的符号相同“-”
并用较大的绝对值减去较小的绝对值
探究新知
异号两数的加法法则二:
绝对值不相等的异号两数相加,取绝对值较大的加数的符号相同,并用较大的绝对值减去较小的绝对值
练一练:
加数
加数
和的符号
和的绝对值
和
5
7
-5
-7
-5
7
5
-7
填表(想法则、写结果)
+
-
+
-
12
12
2
2
12
-12
2
-2
探究新知
(5)如果小红先向右运动5
m,再向左运动5
m,那么两次运动的最后结果如何?
5
5
5+(-5)=0
归纳总结:
互为相反数的两个数相加,结果为0.
探究新知
(6)如果小红第1
s向右(或左)运动5
m,第2s原地不动,2s后小红从起点向右(或左)运动了5
m.如何用算式表示呢?
5+0=5
(-5)+0=-5
归纳总结:一个数同0相加,仍得这个数.
归纳总结
有理数加法法则:
现在,你们能归纳出有理数加法的运算法则吗?
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
课堂练习
有理数加法运算的一般步骤:
(1)观察:(两数是同号或是异号);
(2)符号:
(确定和的符号);
(3)数值:(最后进行绝对值加减运算).
探究新知
例1:
计算:
(1)(
─
3)+(
─
9);(2)(
─
4.7)+3.9;
解:
(同号两数相加)
(1)(
─
3)+(
─
9)
=
─(
)
=
─
12
3+9
(取与加数相同的符号)
(把绝对值相加)
探究新知
(2)(
─
4.7)+3.9
(异号两数相加)
取绝对值较大的的符号
用较大的绝对值减去较大的绝对值
=
─
(4.7
─
3.9)
=
─
0.8
探究新知
(同号两数相加)
(2)(
─
4.7)+3.9
=
─(
)
=
─
0.8
4.7
─
3.9
(取与加数相同的符号)
(把绝对值相加)
课堂练习
1、计算:
(1)15+(-22);
(2)
(-13)+(-8);
(3)(-0.9)+1.5;
解:(1)15+(-22)
(2)
(-13)+(-8)
=-(22-15)
=-7
=-(13+
8)
=-21
课堂练习
(3)(-0.9)+1.5
=+(1.5-0.9)
=0.6
课堂练习
2.如果|a|=3,
|b|
=5,
求a+b的值.
解:
∵|a|=3,
|b|=5
∴a=±3,
b=±5
当a
、b是同号:
①a
=3,b=5
进,
②a
=
-3
,b=
-5时,
a+b=3+5=8
a+b=-3+(-5)=-(3+5)=-8
探究新知
当a
、b是异号:
③a=
-3
,b=5
时,
④a
=3,b=
-5时,
a+b=-3+5=+(5-3)=2
a+b=3+(-5)=-(5-3)=-2
答:
a+b的值为±8或±2.
课堂小结
今天我们收获哪些知识?
1.有理数的加法法则是什么?
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数。
课堂小结
2.进行有理数的加法运算时需要注意哪几个步骤?
(1)观察:(两数是同号或是异号);
(2)符号:
(确定和的符号);
(3)数值:(最后进行绝对值加减运算).
课外作业
课本第24页
习题1.3
第1题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
1.3.1有理数的加法
第1课时
探究新知
教学重、难点
1.重点:掌握有理数的加法法则,能运用法则进行加法运算.
2.难点:探究异号两数相加的法则.
复习回顾
1.如果向东走5米记作+5米,那么向西走8米记作_____.
2.比较下列各数的大小:
3_____2
3____-2
-3_____2
-3____-2
3.已知a=-8,b=-3
则|a|+|b|=
,
则|a|─|b|=
.
>
>
<
<
-8米
11
5
探究新知
小学学过的加法是
.
正数与正数相加、正数与0相加
第二个加数
第一个加数
正数
0
正数
0
正数+正数
0+正数
0+0
正数+0
引入负数后,加法的类型还有哪几种情况?
负数
负数
正数+负数
0+负数
负数+正数
负数+0
负数+负数
探究新知
2.异号两数相加.
1.同号两数相加.
3.一个数与0相加.
思考:
在上述表格中,有理数加法我们可以化归为几个类型?
探究新知
小红向左右方向运动,我们规定向左为负,向右为正.向右运动5
m记作+5
m,向左运动5
m记作─5
m.
(1)如果小红先向右运动5
m,再向右运动3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
两次运动后,小红向右运动
米用算式来表示:
5
3
(+5)+(+3)=+8米
8
8
1.同号两数相加.
探究新知
(2)如果小红先向左运动5
m,再向左运动3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
两次运动后,小红向左运动
米用算式来表示:
(-5)+(-3)=-8
8
5
3
8
探究新知
(+5)+(+3)=+8
(-5)+(-3)=-8
思考:符号相同的两个数应如何相加呢?有什么发现?
加数符号“+”
加数符号“+”
和的符号“+”
加数符号“-”
加数符号“-”
和的符号“-”
加法法则一:
符号相同的两个数相加,结果的符号不变,绝对值相加.
归纳:
练一练
计算:
1.(+3)+(+7)
2.(-1)+(-3)
3.
-5.8+(-7.2)
探究新知
两次运动后,小红一共向右运动2米用算式来表示:
3
5
2
(3)如果小红先向左运动3
m,再向右运动5
m,那么两次运动的最后结果怎样?如何用算式表示?
(-3)+5=+(5-3)=+2
探究新知
两次运动后,小红一共向左运动2米用算式来表示:
5
3
2
(4)如果小红先向右运动3
m,再向左运动5
m,那么两次运动的最后结果怎样?如何用算式表示?
+3+(-5)
=-(5-3)=-2
探究新知
(-3)+(+5)=+(5-3)
思考:符号相同的两个数应如何相加呢?有什么发现?
加数符号“+”
加数符号“-”
和的符号取绝对值较大的加数的符号相同“+”
并用较大的绝对值减去较小的绝对值
(+3)+(-5)=-(5-3)
加数符号“-”
加数符号“+”
和的符号取绝对值较大的加数的符号相同“-”
并用较大的绝对值减去较小的绝对值
探究新知
异号两数的加法法则二:
绝对值不相等的异号两数相加,取绝对值较大的加数的符号相同,并用较大的绝对值减去较小的绝对值
练一练:
加数
加数
和的符号
和的绝对值
和
5
7
-5
-7
-5
7
5
-7
填表(想法则、写结果)
+
-
+
-
12
12
2
2
12
-12
2
-2
探究新知
(5)如果小红先向右运动5
m,再向左运动5
m,那么两次运动的最后结果如何?
5
5
5+(-5)=0
归纳总结:
互为相反数的两个数相加,结果为0.
探究新知
(6)如果小红第1
s向右(或左)运动5
m,第2s原地不动,2s后小红从起点向右(或左)运动了5
m.如何用算式表示呢?
5+0=5
(-5)+0=-5
归纳总结:一个数同0相加,仍得这个数.
归纳总结
有理数加法法则:
现在,你们能归纳出有理数加法的运算法则吗?
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
课堂练习
有理数加法运算的一般步骤:
(1)观察:(两数是同号或是异号);
(2)符号:
(确定和的符号);
(3)数值:(最后进行绝对值加减运算).
探究新知
例1:
计算:
(1)(
─
3)+(
─
9);(2)(
─
4.7)+3.9;
解:
(同号两数相加)
(1)(
─
3)+(
─
9)
=
─(
)
=
─
12
3+9
(取与加数相同的符号)
(把绝对值相加)
探究新知
(2)(
─
4.7)+3.9
(异号两数相加)
取绝对值较大的的符号
用较大的绝对值减去较大的绝对值
=
─
(4.7
─
3.9)
=
─
0.8
探究新知
(同号两数相加)
(2)(
─
4.7)+3.9
=
─(
)
=
─
0.8
4.7
─
3.9
(取与加数相同的符号)
(把绝对值相加)
课堂练习
1、计算:
(1)15+(-22);
(2)
(-13)+(-8);
(3)(-0.9)+1.5;
解:(1)15+(-22)
(2)
(-13)+(-8)
=-(22-15)
=-7
=-(13+
8)
=-21
课堂练习
(3)(-0.9)+1.5
=+(1.5-0.9)
=0.6
课堂练习
2.如果|a|=3,
|b|
=5,
求a+b的值.
解:
∵|a|=3,
|b|=5
∴a=±3,
b=±5
当a
、b是同号:
①a
=3,b=5
进,
②a
=
-3
,b=
-5时,
a+b=3+5=8
a+b=-3+(-5)=-(3+5)=-8
探究新知
当a
、b是异号:
③a=
-3
,b=5
时,
④a
=3,b=
-5时,
a+b=-3+5=+(5-3)=2
a+b=3+(-5)=-(5-3)=-2
答:
a+b的值为±8或±2.
课堂小结
今天我们收获哪些知识?
1.有理数的加法法则是什么?
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数。
课堂小结
2.进行有理数的加法运算时需要注意哪几个步骤?
(1)观察:(两数是同号或是异号);
(2)符号:
(确定和的符号);
(3)数值:(最后进行绝对值加减运算).
课外作业
课本第24页
习题1.3
第1题
https://www.21cnjy.com/help/help_extract.php
