人教版八年级上册 数学 课件: 11.3.2多边形的内角和(共23张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 课件: 11.3.2多边形的内角和(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 18:03:37 | ||
图片预览


文档简介
(共23张PPT)
多边形的内角和
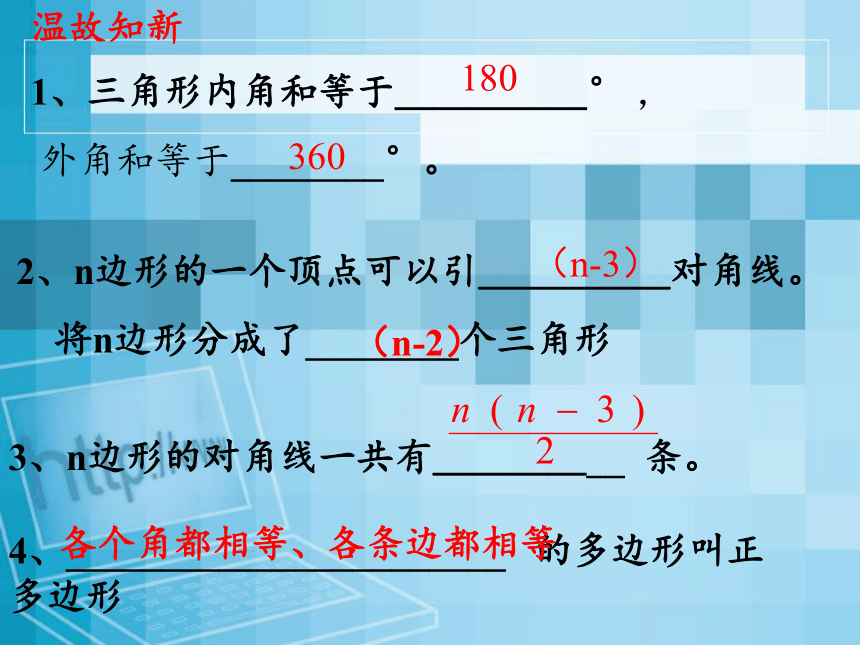
2、n边形的一个顶点可以引_____对角线。
将n边形分成了________个三角形
3、n边形的对角线一共有______
条。
(n-3)
(n-2)
温故知新
1、三角形内角和等于_____°
,
外角和等于________°。
360
180
4、_______________________
的多边形叫正多边形
各个角都相等、各条边都相等
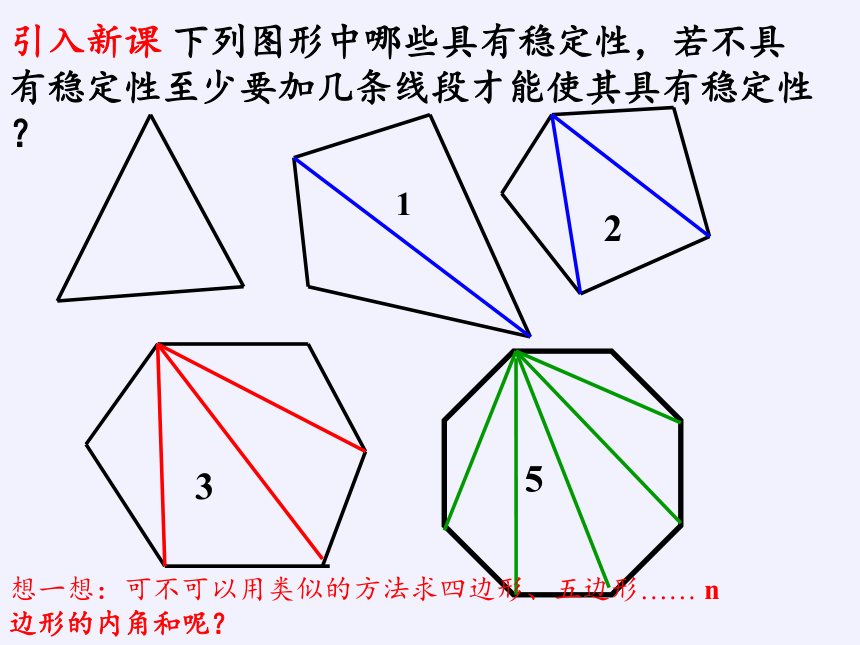
引入新课
下列图形中哪些具有稳定性,若不具有稳定性至少要加几条线段才能使其具有稳定性?
1
2
3
5
想一想:可不可以用类似的方法求四边形、五边形……
n边形的内角和呢?
B
A
C
D
E
合作探究1
五边形内角和=3×180°=540°
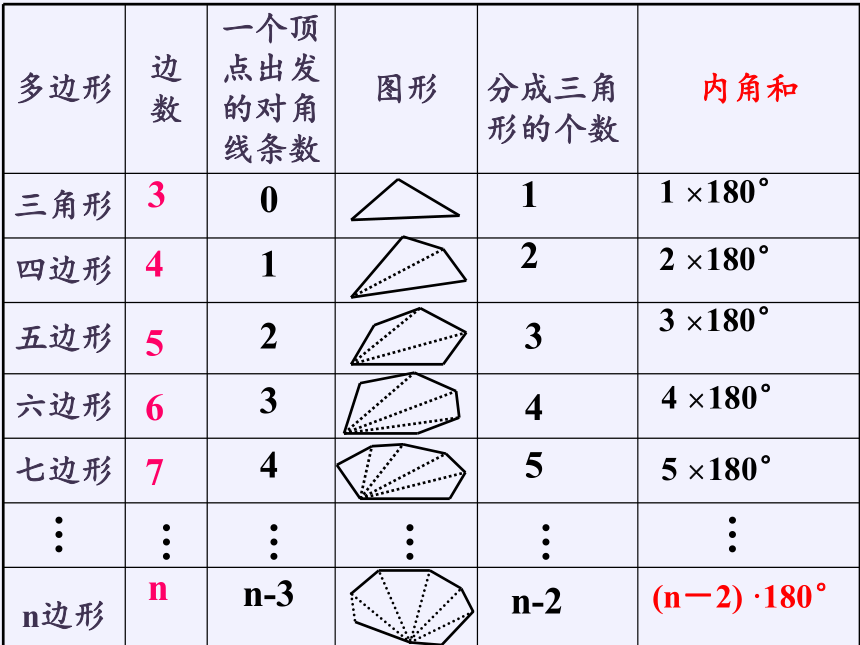
多边形
边数
一个顶点出发的对角线条数
图形
分成三角形的个数
内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2)
·180°
5
×180°
4
×180°
3
×180°
2
×180°
1
×180°
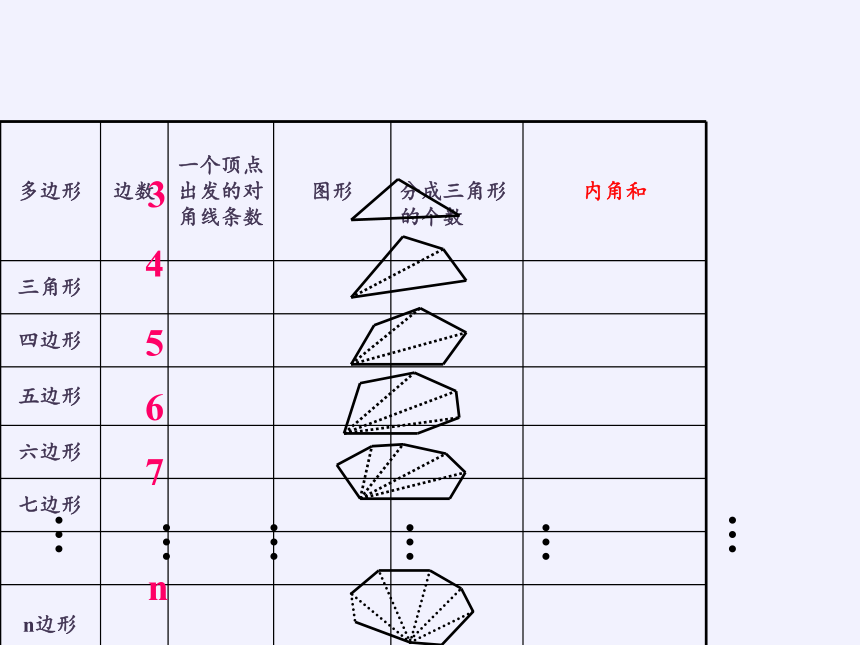
多边形
边数
一个顶点出发的对角线条数
图形
分成三角形的个数
内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
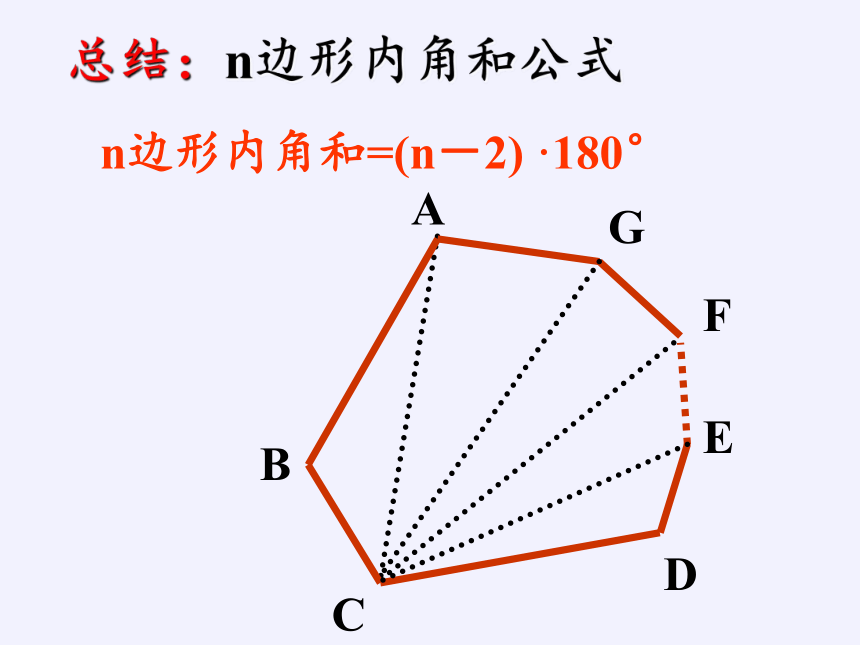
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
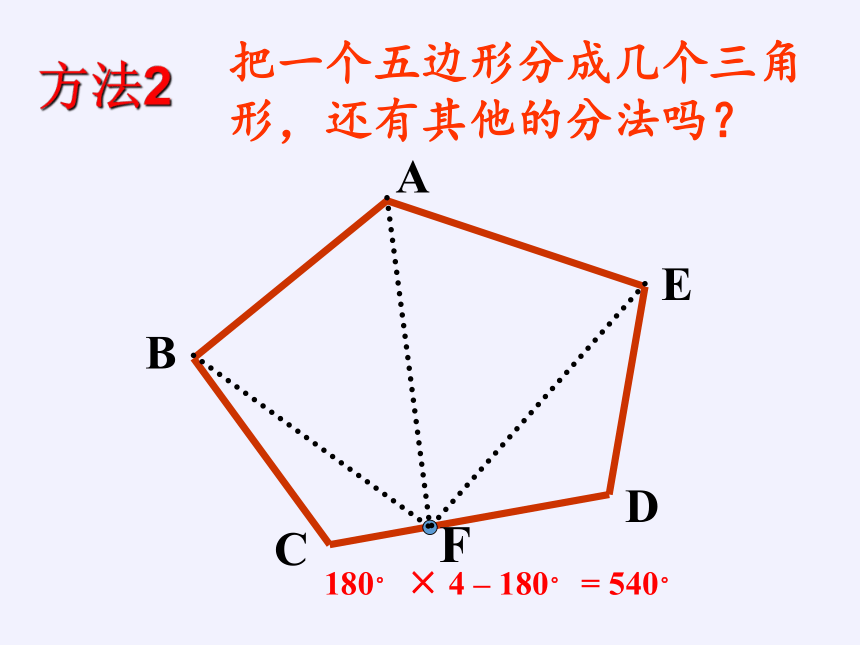
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°
×
4
–
180°
=
540°
方法2
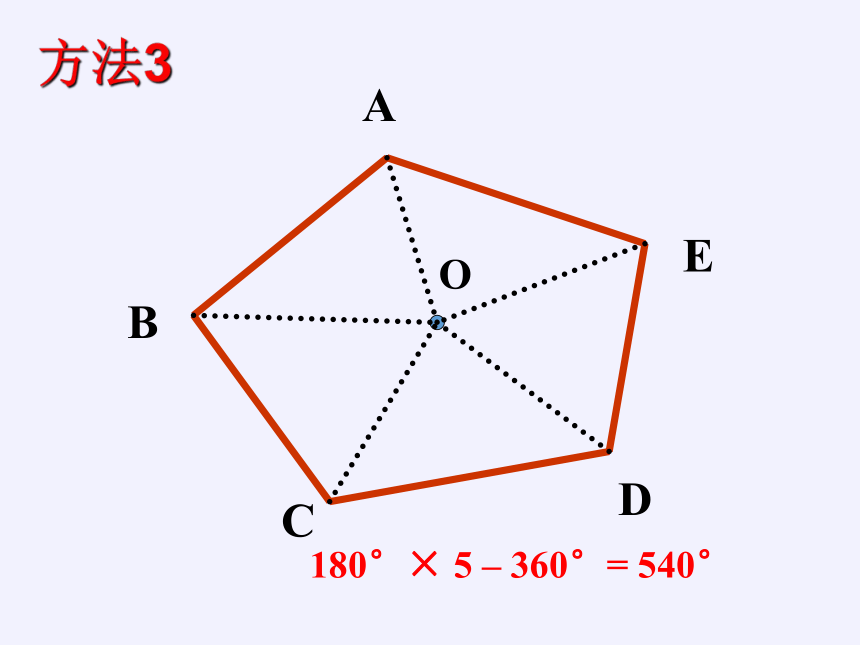
E
A
B
C
D
O
方法3
180°×
5
–
360°=
540°
方法4
A
B
D
E
4
×
180°-180
°
O
=540°
方法4
A
B
C
D
E
O
=540°
n边形内角和公式的应用
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
应用举例:已知四边形ABCD,
∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
分析:四边形的一组对角互补,另一组对角也互补。
解:四边形的内角和为:
(4-2)
×180
=360
°
∴
∠B+∠D=
360
-
(A+∠C)=180°
∠A+∠C=180°
十二边形的内角和是(
)。
一个多边形当边数增加1时,它的内角和增加(
)。
一个多边形的内角和是720?,则此多边形共有(
)个内角。
如果一个多边形的内角和是1440度,那么这是(
)边形。
1800?
180?
六
十
巩固提高
5.
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360?,
∴
(n-2)?180°=2×
360?。
解得:
n=6
∴这个多边形的边数为6。
合作探究2:
1.如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
五边形外角和
结论:五边形的外角和等于360°
-(5-2)
×
180°
=360
°
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
2.在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?
每个内角的度数是
或
每个外角的度数是
n-
练一练
练习1:正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
拓展延伸
(1)n边形最多有______个锐角.
(2)把一个四边形削去一个角,剩下一
个几边形?它的内角和是多少?
课堂小结:
本节课你有哪些收获?请从知识、方法、情感三个方面谈一谈。
达标反馈
(1)一个多边形的内角和为4320°,则它的边数为______
(2)五边形的内角和为_____,它的对角线共有_____条
(3)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(4)一个多边形的每一个内角都等于135°,则这个多边形为_____边形
(5)如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
布置作业
书上25页:8、9、10
谢
谢
多边形的内角和
2、n边形的一个顶点可以引_____对角线。
将n边形分成了________个三角形
3、n边形的对角线一共有______
条。
(n-3)
(n-2)
温故知新
1、三角形内角和等于_____°
,
外角和等于________°。
360
180
4、_______________________
的多边形叫正多边形
各个角都相等、各条边都相等
引入新课
下列图形中哪些具有稳定性,若不具有稳定性至少要加几条线段才能使其具有稳定性?
1
2
3
5
想一想:可不可以用类似的方法求四边形、五边形……
n边形的内角和呢?
B
A
C
D
E
合作探究1
五边形内角和=3×180°=540°
多边形
边数
一个顶点出发的对角线条数
图形
分成三角形的个数
内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2)
·180°
5
×180°
4
×180°
3
×180°
2
×180°
1
×180°
多边形
边数
一个顶点出发的对角线条数
图形
分成三角形的个数
内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°
×
4
–
180°
=
540°
方法2
E
A
B
C
D
O
方法3
180°×
5
–
360°=
540°
方法4
A
B
D
E
4
×
180°-180
°
O
=540°
方法4
A
B
C
D
E
O
=540°
n边形内角和公式的应用
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
应用举例:已知四边形ABCD,
∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
分析:四边形的一组对角互补,另一组对角也互补。
解:四边形的内角和为:
(4-2)
×180
=360
°
∴
∠B+∠D=
360
-
(A+∠C)=180°
∠A+∠C=180°
十二边形的内角和是(
)。
一个多边形当边数增加1时,它的内角和增加(
)。
一个多边形的内角和是720?,则此多边形共有(
)个内角。
如果一个多边形的内角和是1440度,那么这是(
)边形。
1800?
180?
六
十
巩固提高
5.
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360?,
∴
(n-2)?180°=2×
360?。
解得:
n=6
∴这个多边形的边数为6。
合作探究2:
1.如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
五边形外角和
结论:五边形的外角和等于360°
-(5-2)
×
180°
=360
°
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
2.在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?
每个内角的度数是
或
每个外角的度数是
n-
练一练
练习1:正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
拓展延伸
(1)n边形最多有______个锐角.
(2)把一个四边形削去一个角,剩下一
个几边形?它的内角和是多少?
课堂小结:
本节课你有哪些收获?请从知识、方法、情感三个方面谈一谈。
达标反馈
(1)一个多边形的内角和为4320°,则它的边数为______
(2)五边形的内角和为_____,它的对角线共有_____条
(3)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(4)一个多边形的每一个内角都等于135°,则这个多边形为_____边形
(5)如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
布置作业
书上25页:8、9、10
谢
谢
