人教版八年级上册第十二章 全等三角形 12.3 角的平分线的性质 同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级上册第十二章 全等三角形 12.3 角的平分线的性质 同步练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览




文档简介
角的平分线的性质
同步练习
一.选择题(共12小题)
1.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果△ADE的周长为6cm,AC=4cm,那么AD等于( )
A.2cm
B.4cm
C.3cm
D.6cm
2.如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边垂直平分线的交点处
3.如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.
上述结论中,正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
4.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到直线AC的距离为4,则点P到直线AB的距离为( )
A.4
B.3
C.2
D.1
5.如图,已知点P到△ABC三边的距离相等,DE∥AC,AB=8.1cm,BC=6cm,△BDE的周长为( )cm.
A.12
B.14.1
C.16.2
D.7.05
6.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3
B.4
C.5
D.6
7.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4
B.6
C.8
D.10
8.如图,BD是△ABC的角平分线,DE⊥AB于E,△ABC的面积是15,AB=9,BC=6,则DE的长为( )
A.1
B.3
C.2
D.4
9.如图,在△ABC中,AD平分∠BAC交BC于点D,点E在AD上,如果∠ABE=∠C,AE=2ED,那么△ABE与△ADC的周长比为( )
A.1:2
B.2:3
C.1:4
D.4:9
10.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于0.5MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=5,AB=12,则△ABD的面积是( )
A.15
B.30
C.45
D.60
11.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
A.①②③
B.①②④
C.①③④
D.①②③④
12.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE:S△ACD=BD:AC,其中正确的个数为( )
A.5个
B.4个
C.3个
D.2个
二.填空题(共5小题)
13.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若∠ACB=60°,则∠EDC=
.
14.如图,在△ABC中,∠B=45°,∠C=30°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若BD=,则CD的长为
.
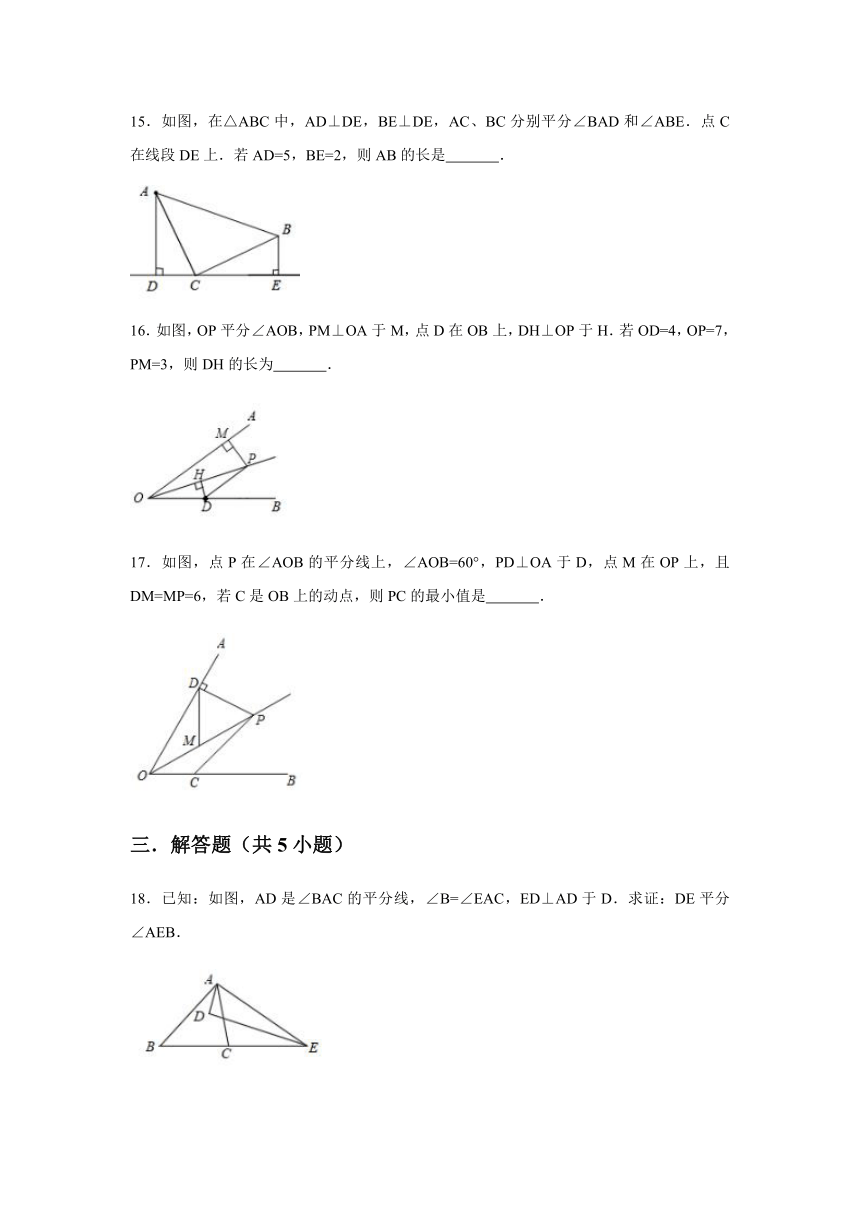
15.如图,在△ABC中,AD⊥DE,BE⊥DE,AC、BC分别平分∠BAD和∠ABE.点C在线段DE上.若AD=5,BE=2,则AB的长是
.
16.如图,OP平分∠AOB,PM⊥OA于M,点D在OB上,DH⊥OP于H.若OD=4,OP=7,PM=3,则DH的长为
.
17.如图,点P在∠AOB的平分线上,∠AOB=60°,PD⊥OA于D,点M在OP上,且DM=MP=6,若C是OB上的动点,则PC的最小值是
.
三.解答题(共5小题)
18.已知:如图,AD是∠BAC的平分线,∠B=∠EAC,ED⊥AD于D.求证:DE平分∠AEB.
19.如图直线EF∥GH,点A、点B分别在EF、GH上,连接AB,∠FAB的角平分线AD交GH于D,过点D作DC⊥AB交AB延长线于点C,若∠CAD=36°,求∠BDC的度数.
20.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.
(1)求∠B的度数.
(2)若DE=5,求BC的长.
21.如图,已知△ABC的周长是21,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.
(1)试判断线段OD、OE、OF的大小关系.
(2)求△ABC的面积.
22.(1)如图1,在△ABC中,AD平分∠BAC交BC于D,DE⊥AB于E,DF⊥AC于F,则有相等关系DE=DF,AE=AF.
(2)如图2,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB、AC相交于M、N两点,其它条件不变,那么又有相等关系AM+
=2AF,请加以证明.
(3)如图3,在Rt△ABC中,∠C=90°,∠BAC=60°,AC=6,AD平分∠BAC交BC于D,∠MDN=120°,ND∥AB,求四边形AMDN的周长.
参考答案
1-5:AADAB
6-10:DDCBB
11-12:DC
13、30°
14、2
15、7
6
18、延长AD交BC于F,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED平分∠AEB.
19、:∵∠FAB的角平分线AD,∠CAD=36°,
∴∠DAF=∠CAD=36°,
∵DC⊥AB,
∴∠ACD=90°,
∴∠ADC=90°-36°=54°,
∵EF∥GH,
∴∠ADB=∠DAF=36°,
∴∠BDC=∠ADC-∠ADB=54°-36°=18°.
20、:(1)∵DE⊥AB于点E,E为AB的中点,
∴DE是线段AB的垂直平分线,
∴DA=DB,
∴∠2=∠B,
∵∠C=90°,
∴∠B=∠1=∠2=30°;
(2)∵DE⊥AB,∠B=30°,
∴BD=2DE=10,
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE=5,
∴BC=CD+BD=15.
21、:(1)OD=OE=OF.
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,
∴OE=OD=3,OF=OD=3,
∴OD=OE=OF;
(2)△ABC的面积=×(AB+AC+BC)×OD=×21×3=31.5.
22、(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△ADE和△ADF中,
∴△ADE≌△ADF(AAS),
∴DE=DF,AE=AF;
(2)解:AM+AN=2AF;
证明如下:由(1)得DE=DF,
∵∠MDN=∠EDF,
∴∠MDE=∠NDF,
在△MDE和△NDF中,
∴△MDE≌△NDF(ASA),
∴ME=NF,
∴AM+AN=(AE+ME)+(AF-NF)=AE+AF=2AF;
(3)由(2)可知AM+AN=2AC=2×6=12,
∵∠BAC=60°,AD平分∠BAC交BC于D,
∴∠BAD=∠CAD=30°,
∵ND∥AB,
∴∠ADN=∠BAD=30°,
∴∠CAD=∠ADN,
∴AN=DN,
在Rt△CDN中,DN=2CN,
∵AC=6,
∴DN=AN==4,
∵∠BAC=60°,∠MDN=120°,
∴∠CDE=∠MDN,
∴DM=DN=4,
∴四边形AMDN的周长=12+4×2=20
同步练习
一.选择题(共12小题)
1.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果△ADE的周长为6cm,AC=4cm,那么AD等于( )
A.2cm
B.4cm
C.3cm
D.6cm
2.如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边垂直平分线的交点处
3.如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.
上述结论中,正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
4.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到直线AC的距离为4,则点P到直线AB的距离为( )
A.4
B.3
C.2
D.1
5.如图,已知点P到△ABC三边的距离相等,DE∥AC,AB=8.1cm,BC=6cm,△BDE的周长为( )cm.
A.12
B.14.1
C.16.2
D.7.05
6.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3
B.4
C.5
D.6
7.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4
B.6
C.8
D.10
8.如图,BD是△ABC的角平分线,DE⊥AB于E,△ABC的面积是15,AB=9,BC=6,则DE的长为( )
A.1
B.3
C.2
D.4
9.如图,在△ABC中,AD平分∠BAC交BC于点D,点E在AD上,如果∠ABE=∠C,AE=2ED,那么△ABE与△ADC的周长比为( )
A.1:2
B.2:3
C.1:4
D.4:9
10.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于0.5MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=5,AB=12,则△ABD的面积是( )
A.15
B.30
C.45
D.60
11.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
A.①②③
B.①②④
C.①③④
D.①②③④
12.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE:S△ACD=BD:AC,其中正确的个数为( )
A.5个
B.4个
C.3个
D.2个
二.填空题(共5小题)
13.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若∠ACB=60°,则∠EDC=
.
14.如图,在△ABC中,∠B=45°,∠C=30°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若BD=,则CD的长为
.
15.如图,在△ABC中,AD⊥DE,BE⊥DE,AC、BC分别平分∠BAD和∠ABE.点C在线段DE上.若AD=5,BE=2,则AB的长是
.
16.如图,OP平分∠AOB,PM⊥OA于M,点D在OB上,DH⊥OP于H.若OD=4,OP=7,PM=3,则DH的长为
.
17.如图,点P在∠AOB的平分线上,∠AOB=60°,PD⊥OA于D,点M在OP上,且DM=MP=6,若C是OB上的动点,则PC的最小值是
.
三.解答题(共5小题)
18.已知:如图,AD是∠BAC的平分线,∠B=∠EAC,ED⊥AD于D.求证:DE平分∠AEB.
19.如图直线EF∥GH,点A、点B分别在EF、GH上,连接AB,∠FAB的角平分线AD交GH于D,过点D作DC⊥AB交AB延长线于点C,若∠CAD=36°,求∠BDC的度数.
20.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.
(1)求∠B的度数.
(2)若DE=5,求BC的长.
21.如图,已知△ABC的周长是21,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.
(1)试判断线段OD、OE、OF的大小关系.
(2)求△ABC的面积.
22.(1)如图1,在△ABC中,AD平分∠BAC交BC于D,DE⊥AB于E,DF⊥AC于F,则有相等关系DE=DF,AE=AF.
(2)如图2,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB、AC相交于M、N两点,其它条件不变,那么又有相等关系AM+
=2AF,请加以证明.
(3)如图3,在Rt△ABC中,∠C=90°,∠BAC=60°,AC=6,AD平分∠BAC交BC于D,∠MDN=120°,ND∥AB,求四边形AMDN的周长.
参考答案
1-5:AADAB
6-10:DDCBB
11-12:DC
13、30°
14、2
15、7
6
18、延长AD交BC于F,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED平分∠AEB.
19、:∵∠FAB的角平分线AD,∠CAD=36°,
∴∠DAF=∠CAD=36°,
∵DC⊥AB,
∴∠ACD=90°,
∴∠ADC=90°-36°=54°,
∵EF∥GH,
∴∠ADB=∠DAF=36°,
∴∠BDC=∠ADC-∠ADB=54°-36°=18°.
20、:(1)∵DE⊥AB于点E,E为AB的中点,
∴DE是线段AB的垂直平分线,
∴DA=DB,
∴∠2=∠B,
∵∠C=90°,
∴∠B=∠1=∠2=30°;
(2)∵DE⊥AB,∠B=30°,
∴BD=2DE=10,
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DC=DE=5,
∴BC=CD+BD=15.
21、:(1)OD=OE=OF.
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,
∴OE=OD=3,OF=OD=3,
∴OD=OE=OF;
(2)△ABC的面积=×(AB+AC+BC)×OD=×21×3=31.5.
22、(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△ADE和△ADF中,
∴△ADE≌△ADF(AAS),
∴DE=DF,AE=AF;
(2)解:AM+AN=2AF;
证明如下:由(1)得DE=DF,
∵∠MDN=∠EDF,
∴∠MDE=∠NDF,
在△MDE和△NDF中,
∴△MDE≌△NDF(ASA),
∴ME=NF,
∴AM+AN=(AE+ME)+(AF-NF)=AE+AF=2AF;
(3)由(2)可知AM+AN=2AC=2×6=12,
∵∠BAC=60°,AD平分∠BAC交BC于D,
∴∠BAD=∠CAD=30°,
∵ND∥AB,
∴∠ADN=∠BAD=30°,
∴∠CAD=∠ADN,
∴AN=DN,
在Rt△CDN中,DN=2CN,
∵AC=6,
∴DN=AN==4,
∵∠BAC=60°,∠MDN=120°,
∴∠CDE=∠MDN,
∴DM=DN=4,
∴四边形AMDN的周长=12+4×2=20
