人教版 八年级 上册 11.2与三角形有关的角 同步练习(word解析版)
文档属性
| 名称 | 人教版 八年级 上册 11.2与三角形有关的角 同步练习(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 76.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览



文档简介
与三角形有关的角同步练习
一、选择题
若一个三角形的三个内角的度数之比为,则这个三角形是.
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
等腰三角形
在不等边三角形中,最小的角可以是.
A.
B.
C.
D.
在锐角三角形中,最大角的取值范围是.
A.
B.
C.
D.
如图,CE是的外角的平分线,若,,则等于.
A.
B.
C.
D.
下列说法正确的是
A.
三角形的内角中最多有一个锐角
B.
三角形的内角中最多有两个锐角
C.
三角形的内角中最多有一个直角
D.
三角形的三个内角都大于
如图,在中,,沿图中虚线截去,则的度数为
A.
B.
C.
D.
如图,,,,则等于
A.
B.
C.
D.
如图,中,,,则等于
A.
B.
C.
D.
在三角形的三个外角中,钝角的个数最少有.
A.
1个
B.
2个
C.
3个
D.
4个
如图,在中,点D在AB上,点E在AC上,若,,则的大小为
A.
B.
C.
D.
在中,,,的度数之比为,则的度数为
A.
B.
C.
D.
二、填空题
如图,在中,,BD是AC边上的高,则_________.
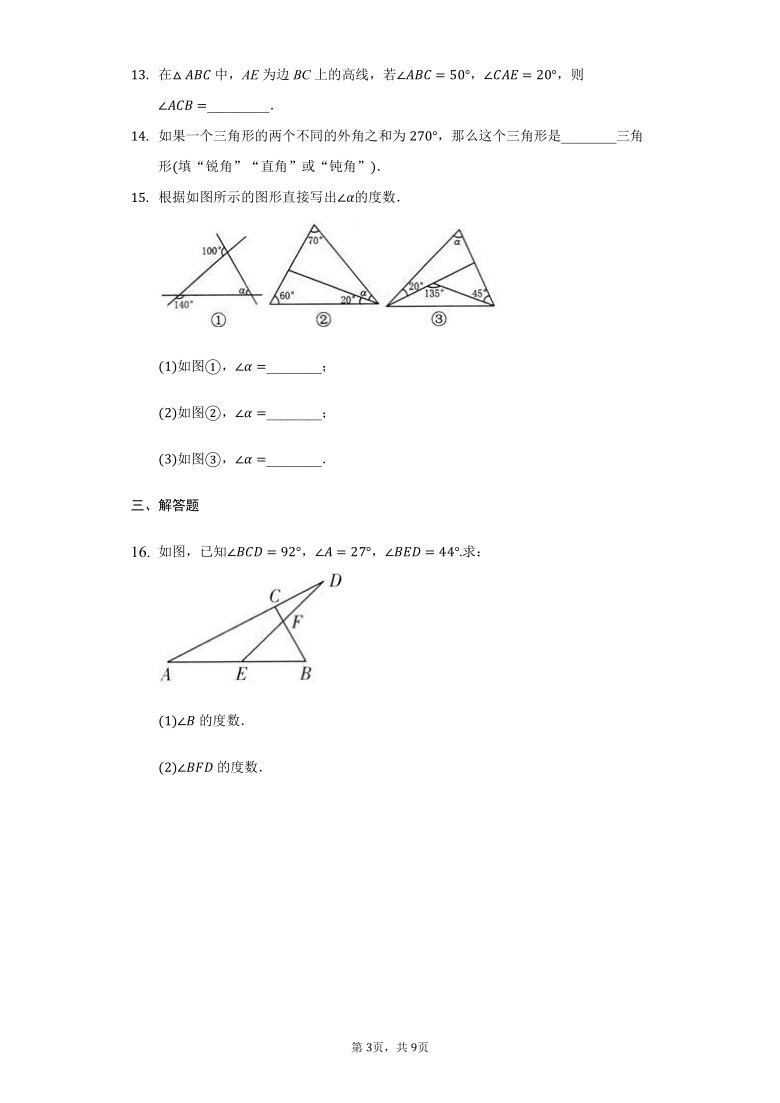
在中,AE为边BC上的高线,若,,则_________.
如果一个三角形的两个不同的外角之和为,那么这个三角形是________三角形填“锐角”“直角”或“钝角”.
根据如图所示的图形直接写出的度数.
如图,________;
如图,________;
如图,________.
三、解答题
如图,已知,,求:
的度数.
的度数.
如图,在中,AD是BC边上的高,AE平分,,,求与的度数.
答案和解析
1.C
解:设其三个内角度数分别是2k,8k,5k.
根据三角形的内角和定理,得:
,
解得:,
,
这个三角形是钝角三角形.
2.D
解:在不等边三角形中,最小的角要小于,否则三内角的和大于.
3.D
解:三角形中最大的角不能小于,如果小于,则三角形的内角和将小于,
又该三角形是锐角三角形,则最大角必须小于,故最大角的取值范围是.
4.C
解:是的外角的平分线,,
,
又,
.
故选C.
5.C
解:A、直角三角形中有两个锐角,故本选项错误;
B、等边三角形的三个角都是锐角,故本选项错误;
C、三角形的内角中最多有一个直角,故本选项正确;
D、若三角形的内角都大于,则三个内角的和大于,这样的三角形不存在,故本选项错误.
6C
解:
作、如上图,
,
,
.
7.C
解:,,
,
8.B
解:由三角形内角和定理得,,
9.B
解:三角形的外角与它相邻的内角互补,在一个三角形中最多有一个钝角,
它的外角至少有两个钝角.
故选B.
10.C
解:,
,
,
,
故选:C.
11.C
解:中:::3:4,?
设,,?
,?
,
解得,
?
故选C.
12.
解:,
,
解得,
,
是AC边上的高,
.
故答案为.
13.或
解:,
,
,
当为锐角时,如图1,
在中,,
,
当为钝角时,如图2,
,
则.
故答案为或
14.直角
解:一个三角形的两个不同的外角之和为,
第三个外角是,
与的外角相邻的内角是,
这个三角形一定是直角三角形.
故答案为直角.
15.;;.
解:
如图,,
,
.
故答案为.
如图,,
,
又,
.
故答案为.
如图,,
,
又,
.
故答案为.
16.解:在中,
,,,
;
在中,
,,,
.
17.解:,,,
,
平分,
,
是BC上的高,
,
,
,
在中,.
第2页,共2页
第1页,共1页
一、选择题
若一个三角形的三个内角的度数之比为,则这个三角形是.
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
等腰三角形
在不等边三角形中,最小的角可以是.
A.
B.
C.
D.
在锐角三角形中,最大角的取值范围是.
A.
B.
C.
D.
如图,CE是的外角的平分线,若,,则等于.
A.
B.
C.
D.
下列说法正确的是
A.
三角形的内角中最多有一个锐角
B.
三角形的内角中最多有两个锐角
C.
三角形的内角中最多有一个直角
D.
三角形的三个内角都大于
如图,在中,,沿图中虚线截去,则的度数为
A.
B.
C.
D.
如图,,,,则等于
A.
B.
C.
D.
如图,中,,,则等于
A.
B.
C.
D.
在三角形的三个外角中,钝角的个数最少有.
A.
1个
B.
2个
C.
3个
D.
4个
如图,在中,点D在AB上,点E在AC上,若,,则的大小为
A.
B.
C.
D.
在中,,,的度数之比为,则的度数为
A.
B.
C.
D.
二、填空题
如图,在中,,BD是AC边上的高,则_________.
在中,AE为边BC上的高线,若,,则_________.
如果一个三角形的两个不同的外角之和为,那么这个三角形是________三角形填“锐角”“直角”或“钝角”.
根据如图所示的图形直接写出的度数.
如图,________;
如图,________;
如图,________.
三、解答题
如图,已知,,求:
的度数.
的度数.
如图,在中,AD是BC边上的高,AE平分,,,求与的度数.
答案和解析
1.C
解:设其三个内角度数分别是2k,8k,5k.
根据三角形的内角和定理,得:
,
解得:,
,
这个三角形是钝角三角形.
2.D
解:在不等边三角形中,最小的角要小于,否则三内角的和大于.
3.D
解:三角形中最大的角不能小于,如果小于,则三角形的内角和将小于,
又该三角形是锐角三角形,则最大角必须小于,故最大角的取值范围是.
4.C
解:是的外角的平分线,,
,
又,
.
故选C.
5.C
解:A、直角三角形中有两个锐角,故本选项错误;
B、等边三角形的三个角都是锐角,故本选项错误;
C、三角形的内角中最多有一个直角,故本选项正确;
D、若三角形的内角都大于,则三个内角的和大于,这样的三角形不存在,故本选项错误.
6C
解:
作、如上图,
,
,
.
7.C
解:,,
,
8.B
解:由三角形内角和定理得,,
9.B
解:三角形的外角与它相邻的内角互补,在一个三角形中最多有一个钝角,
它的外角至少有两个钝角.
故选B.
10.C
解:,
,
,
,
故选:C.
11.C
解:中:::3:4,?
设,,?
,?
,
解得,
?
故选C.
12.
解:,
,
解得,
,
是AC边上的高,
.
故答案为.
13.或
解:,
,
,
当为锐角时,如图1,
在中,,
,
当为钝角时,如图2,
,
则.
故答案为或
14.直角
解:一个三角形的两个不同的外角之和为,
第三个外角是,
与的外角相邻的内角是,
这个三角形一定是直角三角形.
故答案为直角.
15.;;.
解:
如图,,
,
.
故答案为.
如图,,
,
又,
.
故答案为.
如图,,
,
又,
.
故答案为.
16.解:在中,
,,,
;
在中,
,,,
.
17.解:,,,
,
平分,
,
是BC上的高,
,
,
,
在中,.
第2页,共2页
第1页,共1页
