人教版数学 八年级 上册 12.2三角形全等的判定 巩固练习(Word版 含解析)
文档属性
| 名称 | 人教版数学 八年级 上册 12.2三角形全等的判定 巩固练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 106.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 06:50:46 | ||
图片预览


文档简介
三角形全等的判定巩固练习
一、选择题
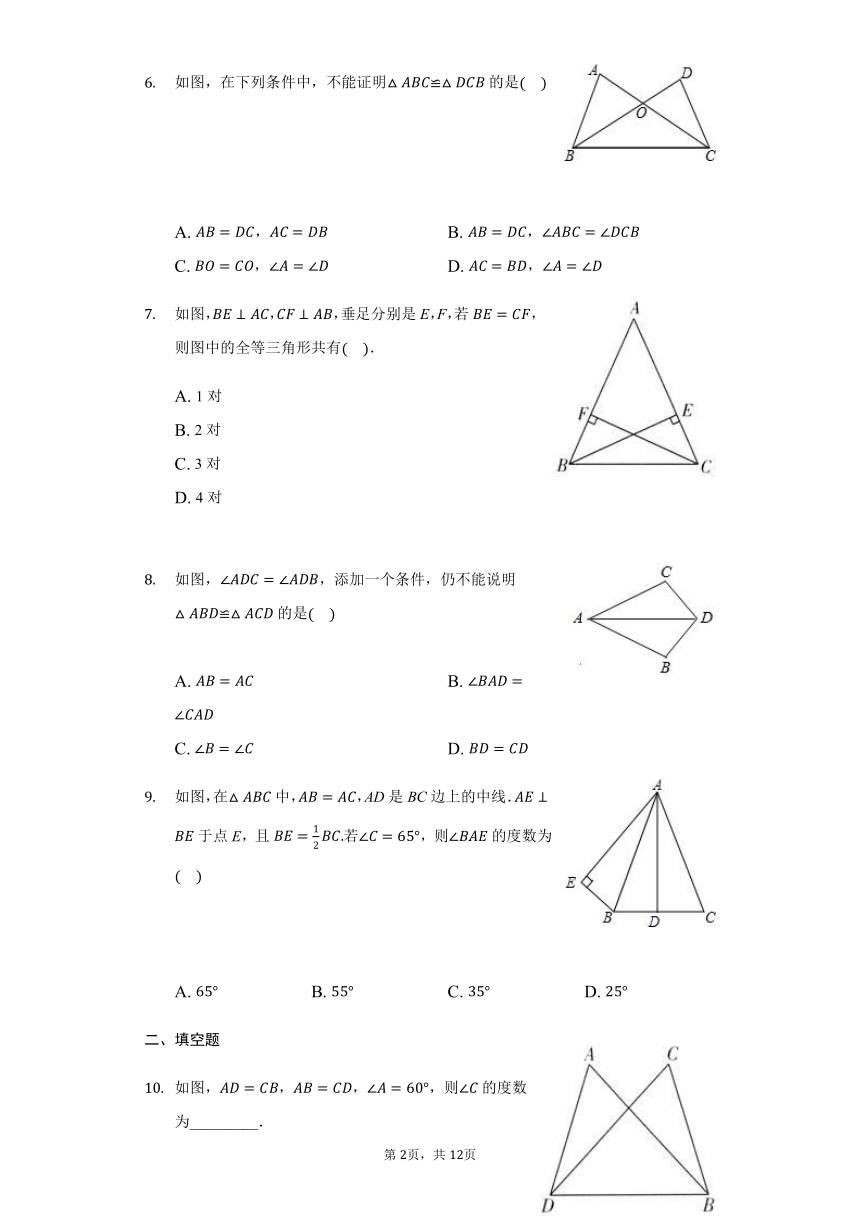
如图,已知,有四个可添加的条件:;;;能使≌的条件有?
?
A.
1个
B.
2个
C.
3个
D.
4个
在和中,,,若要证明≌,还需要补充一个条件,则正确的补充方法是?
?
?
A.
B.
C.
D.
如图,在和中,,,根据“SAS”判定≌,还需添加的条件是.
A.
B.
C.
D.
以上都可以
在和中,已知,,要判定这两个三角形全等,还需要条件.
A.
B.
C.
D.
如图,是等边三角形,若它边上的一点与这边所对角的顶点的连线恰好将分成两个全等三角形,则这样的点共有.
A.
1个
B.
3个
C.
6个
D.
9个
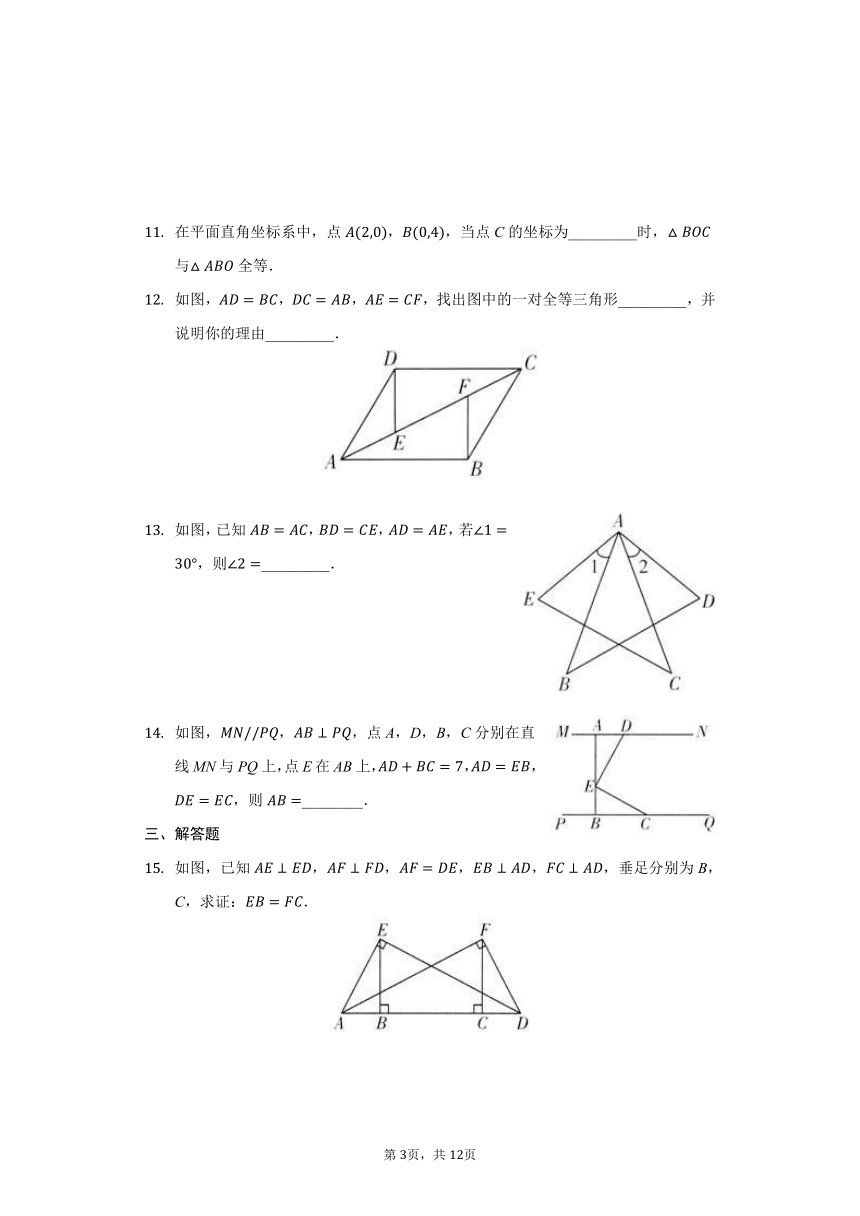
如图,在下列条件中,不能证明≌的是
A.
,
B.
,
C.
,
D.
,
如图,,,垂足分别是E,F,若,则图中的全等三角形共有.
A.
1对
B.
2对
C.
3对
D.
4对
如图,,添加一个条件,仍不能说明≌的是
A.
B.
C.
D.
如图,在中,,AD是BC边上的中线.于点E,且若,则的度数为
A.
B.
C.
D.
二、填空题
如图,,,,则的度数为_________.
在平面直角坐标系中,点,,当点C的坐标为_________时,与全等.
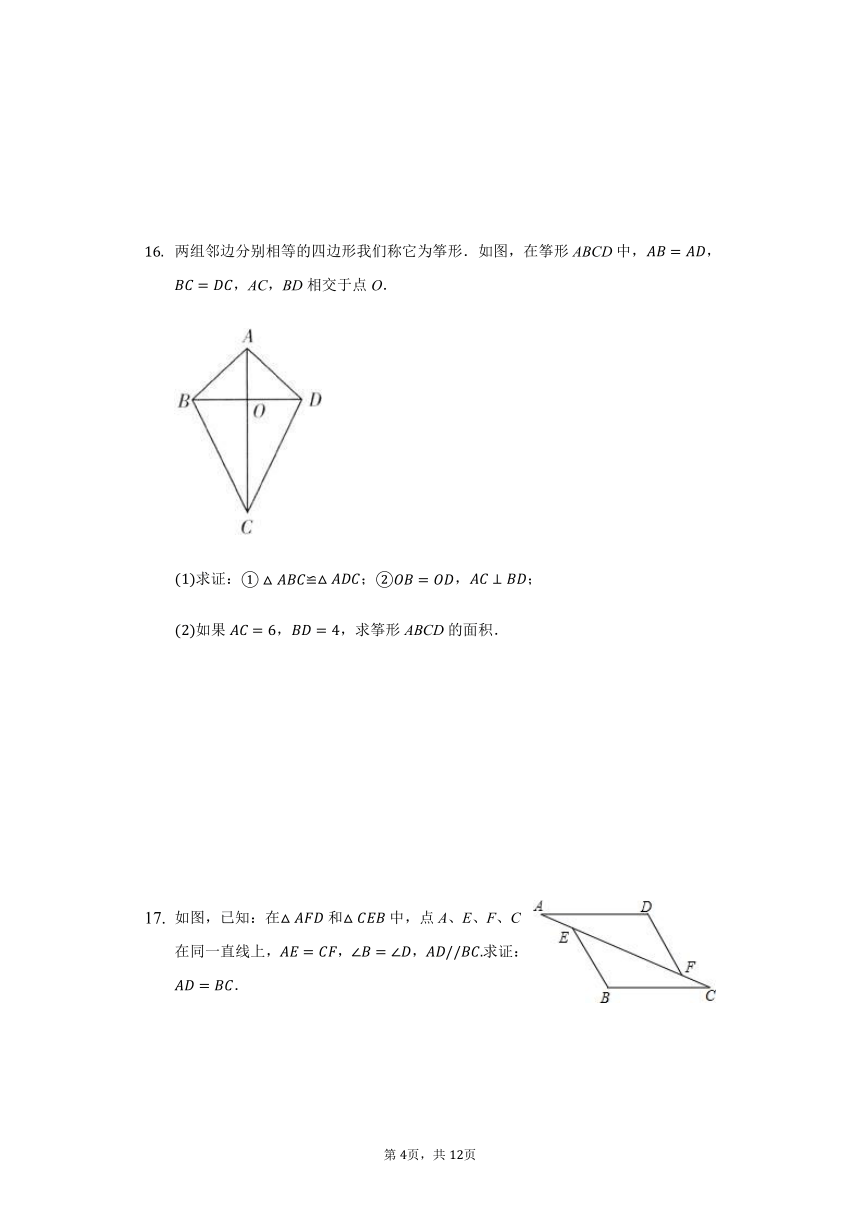
如图,,,,找出图中的一对全等三角形_________,并说明你的理由_________.
如图,已知,,,若,则_________.
如图,,,点A,D,B,C分别在直线MN与PQ上,点E在AB上,,,,则________.
三、解答题
如图,已知,,,,,垂足分别为B,C,求证:.
两组邻边分别相等的四边形我们称它为筝形.如图,在筝形ABCD中,,,AC,BD相交于点O.
求证:≌;,;
如果,,求筝形ABCD的面积.
如图,已知:在和中,点A、E、F、C在同一直线上,,,求证:.
答案和解析
1.D
解:添加,可根据HL判定≌;
添加,可根据HL判定≌;
添加,可根据AAS判定≌;
添加,可根据AAS判定≌.
共有4个可以使≌的条件.
2.D
解:如图所示,
,,再添一组边,
根据SAS就可得出≌,
3.B
解:,,根据“SAS”判定≌,
添的是两边的夹角,夹角为,
4.C
解:已知条件已存在,不符合符合全等三角形的判定定理,无法证明这两个三角形全等,故A项不符合题意;
B.已知条件不是对应边的相等关系,不符合符合全等三角形的判定定理,无法证明这两个三角形全等。故B项不符合题意;
C.在和中中,,,,利用SSS可证明三角形全等,故C项符合题意;
D.SSA不符合符合全等三角形的判定定理,无法证明这两个三角形全等,故D项不符合题意;
5.B
解:如图,D,E,F分别为各边的中点,分别连接AD,BE,试证:
≌,≌,≌.
证明:是等边三角形
为BC边上的中点
,,
≌
同理可证:≌,≌
所以这样的点共有三个.
故选B.
6.D
解:A、,,,符合全等三角形的判定定理“SSS”,即能推出≌,故本选项错误;
B、,,,符合全等三角形的判定定理“SAS”,即能推出≌,故本选项错误;
C、在和中,
,
≌,
,,
,
,
,
在和中,
,
≌,
即能推出≌,故本选项错误;
D、具备条件,,不能推出≌,故本选项正确.
故选D.
7.C
解:
≌,
,,
,
,,
≌;
≌,
,,
,
,
≌
,
,
≌;
≌,
设BE与CF相交于点O,
,,
,
,,
≌.
故选C.
8.A
解:A、添加,利用SSA不能判定≌,故此选项符合题意;
B、添加,利用ASA能判定≌,故此选项不合题意;
C、添加,利用AAS能判定≌,故此选项不合题意;
D、添加,可利用SAS能判定≌,故此选项不合题意;
故选:A.
9.D
解:,,
,,,,
在中,,,
,
,
又.
,
又,
≌,
,
10.
解:在和中,
≌,
,
,
,
故答案为.
11.或或
解:如图所示:
有三个点符合,?
点,,
,,
与全等,
,,
,,.
故答案为或或.
12.答案不唯一,如≌理由:根据“SSS”,即,,.
解:在和中,
≌.
故答案为答案不唯一,如≌理由:根据“SSS”,即,,.
13.
解:在和中,
≌,
,
,
故答案为.
14.7
?解:,,
,
,
在和中,
,,
≌,
,
,
.
故答案为7.
15.证明:,,
.
,,
≌,
,.
,,
.
在和中,
≌.
.
16.解:,,,
≌.
由知,
又,,
≌.
,,
,
,
.
筝形ABCD的面积的面积的面积.
17.证明:,
,
,
,
即,
在和中
,
≌,
.
第2页,共2页
第1页,共1页
一、选择题
如图,已知,有四个可添加的条件:;;;能使≌的条件有?
?
A.
1个
B.
2个
C.
3个
D.
4个
在和中,,,若要证明≌,还需要补充一个条件,则正确的补充方法是?
?
?
A.
B.
C.
D.
如图,在和中,,,根据“SAS”判定≌,还需添加的条件是.
A.
B.
C.
D.
以上都可以
在和中,已知,,要判定这两个三角形全等,还需要条件.
A.
B.
C.
D.
如图,是等边三角形,若它边上的一点与这边所对角的顶点的连线恰好将分成两个全等三角形,则这样的点共有.
A.
1个
B.
3个
C.
6个
D.
9个
如图,在下列条件中,不能证明≌的是
A.
,
B.
,
C.
,
D.
,
如图,,,垂足分别是E,F,若,则图中的全等三角形共有.
A.
1对
B.
2对
C.
3对
D.
4对
如图,,添加一个条件,仍不能说明≌的是
A.
B.
C.
D.
如图,在中,,AD是BC边上的中线.于点E,且若,则的度数为
A.
B.
C.
D.
二、填空题
如图,,,,则的度数为_________.
在平面直角坐标系中,点,,当点C的坐标为_________时,与全等.
如图,,,,找出图中的一对全等三角形_________,并说明你的理由_________.
如图,已知,,,若,则_________.
如图,,,点A,D,B,C分别在直线MN与PQ上,点E在AB上,,,,则________.
三、解答题
如图,已知,,,,,垂足分别为B,C,求证:.
两组邻边分别相等的四边形我们称它为筝形.如图,在筝形ABCD中,,,AC,BD相交于点O.
求证:≌;,;
如果,,求筝形ABCD的面积.
如图,已知:在和中,点A、E、F、C在同一直线上,,,求证:.
答案和解析
1.D
解:添加,可根据HL判定≌;
添加,可根据HL判定≌;
添加,可根据AAS判定≌;
添加,可根据AAS判定≌.
共有4个可以使≌的条件.
2.D
解:如图所示,
,,再添一组边,
根据SAS就可得出≌,
3.B
解:,,根据“SAS”判定≌,
添的是两边的夹角,夹角为,
4.C
解:已知条件已存在,不符合符合全等三角形的判定定理,无法证明这两个三角形全等,故A项不符合题意;
B.已知条件不是对应边的相等关系,不符合符合全等三角形的判定定理,无法证明这两个三角形全等。故B项不符合题意;
C.在和中中,,,,利用SSS可证明三角形全等,故C项符合题意;
D.SSA不符合符合全等三角形的判定定理,无法证明这两个三角形全等,故D项不符合题意;
5.B
解:如图,D,E,F分别为各边的中点,分别连接AD,BE,试证:
≌,≌,≌.
证明:是等边三角形
为BC边上的中点
,,
≌
同理可证:≌,≌
所以这样的点共有三个.
故选B.
6.D
解:A、,,,符合全等三角形的判定定理“SSS”,即能推出≌,故本选项错误;
B、,,,符合全等三角形的判定定理“SAS”,即能推出≌,故本选项错误;
C、在和中,
,
≌,
,,
,
,
,
在和中,
,
≌,
即能推出≌,故本选项错误;
D、具备条件,,不能推出≌,故本选项正确.
故选D.
7.C
解:
≌,
,,
,
,,
≌;
≌,
,,
,
,
≌
,
,
≌;
≌,
设BE与CF相交于点O,
,,
,
,,
≌.
故选C.
8.A
解:A、添加,利用SSA不能判定≌,故此选项符合题意;
B、添加,利用ASA能判定≌,故此选项不合题意;
C、添加,利用AAS能判定≌,故此选项不合题意;
D、添加,可利用SAS能判定≌,故此选项不合题意;
故选:A.
9.D
解:,,
,,,,
在中,,,
,
,
又.
,
又,
≌,
,
10.
解:在和中,
≌,
,
,
,
故答案为.
11.或或
解:如图所示:
有三个点符合,?
点,,
,,
与全等,
,,
,,.
故答案为或或.
12.答案不唯一,如≌理由:根据“SSS”,即,,.
解:在和中,
≌.
故答案为答案不唯一,如≌理由:根据“SSS”,即,,.
13.
解:在和中,
≌,
,
,
故答案为.
14.7
?解:,,
,
,
在和中,
,,
≌,
,
,
.
故答案为7.
15.证明:,,
.
,,
≌,
,.
,,
.
在和中,
≌.
.
16.解:,,,
≌.
由知,
又,,
≌.
,,
,
,
.
筝形ABCD的面积的面积的面积.
17.证明:,
,
,
,
即,
在和中
,
≌,
.
第2页,共2页
第1页,共1页
