人教版数学八年级上册 12.2 三角形全等的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版数学八年级上册 12.2 三角形全等的判定 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 190.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 06:57:09 | ||
图片预览




文档简介
三角形全等的判定
同步练习
一.选择题(共12小题)
1.如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达A和B的点C,分别延长AC,BC到D,E,使CD=CA,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是( )
A.SSS
B.ASA
C.AAS
D.SAS
2.下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,AB=DE
D.∠B=∠E,∠C=∠F,AC=DF
3.如图,已知∠ABC=∠DCB,添加以下条件,不能使△ABC≌△DCB的是( )
A.AB=DC
B.∠A=∠D
C.AC=DB
D.∠ACB=∠DBC
4.如图,AE∥FD,AE=DF,要使△EAB≌△FDC,需要添加的条件可以是( )
A.AB=BC
B.EB=FC
C.∠A=∠F
D.AB=CD
5.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E
B.AC=DF
C.∠ACD=∠BFE
D.BF=CD
6.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=6cm,OC=4cm,则OB的长为( )
A.2cm
B.3cm
C.4cm
D.6cm
7.如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:其中正确的结论有( )
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A.2个
B.3个
C.4个
D.5个
8.如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF;③BD=CE.两两组合在一起,共有三种组合:
(1)①②(2)①③(3)②③问能判定AB=AC的组合的是( )
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(1)(2)(3)
9.如图,线段AB与CD相交于点O,AO=BO,CO=DO,BC⊥CD,若BC=6,AC=10,则CD的长为( )
A.6
B.7
C.8
D.9
10.如图,已知AB=CD且AB⊥CD,连接AD,分别过点C,B作CE⊥AD,BF⊥AD,垂足分别为E,F.若AD=10,CE=8,BF=6,则EF的长为( )
A.4
B.3.5
C.3
D.2.5
11.已知:如图,AD是△ABC的中线,∠1=2∠2,CE⊥AD,BF⊥AD,点E、F为垂足,EF=6cm,则BC的长为( )
A.6cm
B.12cm
C.18cm
D.24cm
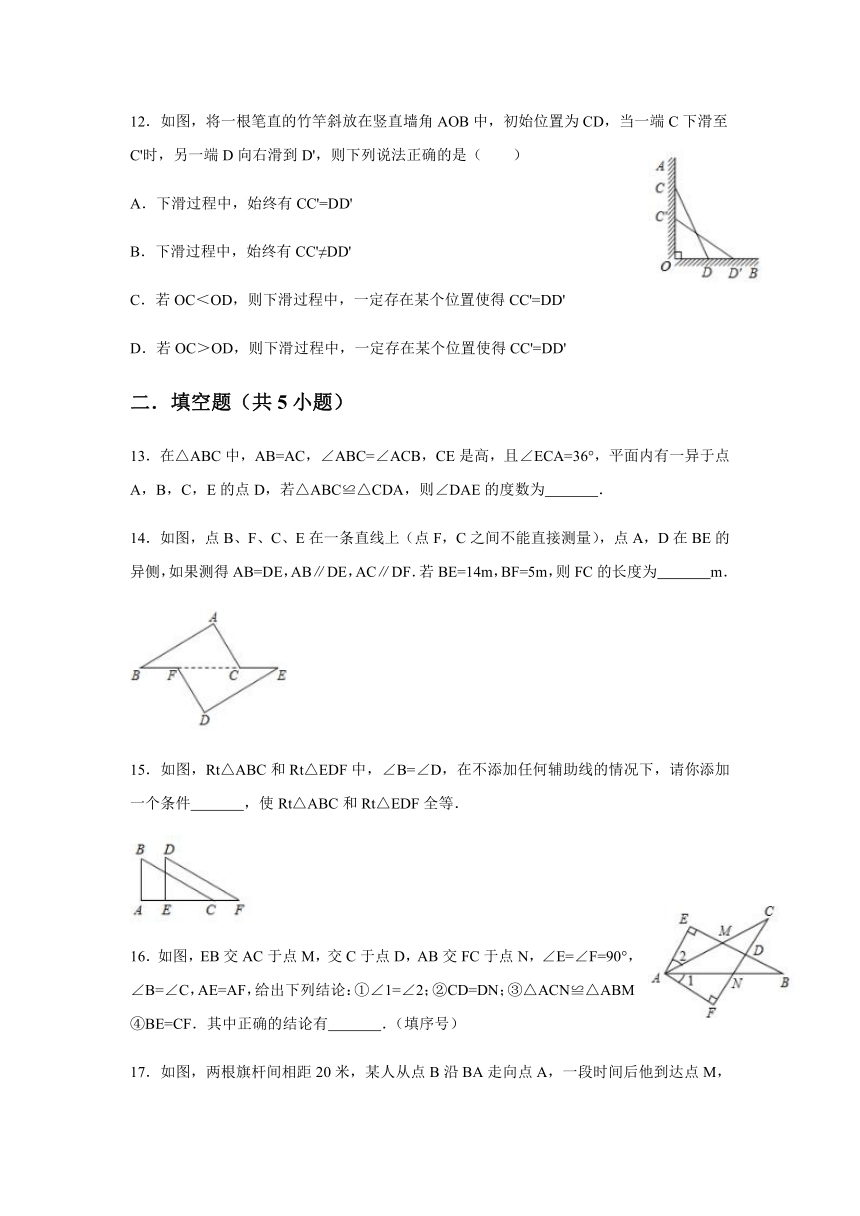
12.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
二.填空题(共5小题)
13.在△ABC中,AB=AC,∠ABC=∠ACB,CE是高,且∠ECA=36°,平面内有一异于点A,B,C,E的点D,若△ABC≌△CDA,则∠DAE的度数为
.
14.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为
m.
15.如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
16.如图,EB交AC于点M,交C于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有
.(填序号)
17.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
三.解答题(共5小题)
18.如图,A、C、D三点共线,△ABC和△CDE落在AD的同侧,AC=CE,∠B=∠BCE=∠CDE.求证:AB=CD.
19.如图AB=AD,AC=AE,∠BAE=∠DAC.
求证:(1)∠C=∠E;
(2)AM=AN.
20.如图,点A,F,D,C在同一直线上,BC,EF交于点M,∠B=∠E=90°,AF=CD,AB=DE.
求证:(1)Rt△ABC≌Rt△DEF;(2)MF=MC.
21.如图,AD为△ABC的中线,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF.
(1)求证;DE⊥DF;(2)求证:△BDE≌△DCF;(3)求证:EF∥BC.
22.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
参考答案
1-5:DDCDD
6-10:ACCCA
11-12:BD
13、117°、27°、72°和81°
14、4
:AB=ED
,①③④.
4
18、:∵∠BCD=∠A+∠B=∠BCE+∠DCE,∠B=∠BCE,
∴∠A=∠ECD,
在△ABC和△CDE中,
∴△ABC≌△CDE(AAS),
∴AB=CD.
19、:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS),
∴∠C=∠E;
(2)∵△ABC≌△ADE,
∴∠B=∠D,
在△ABM和△ADN中,
∴△ABM≌△ADN(ASA),
∴AM=AN.
20、(1)证明:∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF,
∵∠B=∠E=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL);
(2)证明:由(1)知,Rt△ABC≌Rt△DEF,
∴∠BCA=∠EFD,
∴∠MCF=∠MFC,
∴MF=MC.
21、:(1)∵DE平分∠ADB,DF平分∠ADC,
∴∠PDE=∠ADB,∠FDP=∠ADC,
∴∠EDF=∠PDE+∠PDF=∠ADB+∠ADC=(∠ADB+∠ADC)=90°,
∴DE⊥DF;
(2)∵BE⊥DE,DF⊥CF,
∴∠BED=∠DFC=90°,
∵∠BDE+∠CDF=90°,∠CDF+∠DCF=90°,
∴∠BDE=∠DCF,
∴DE∥CF,
∵D是BC中点,
∴BD=DC,
在△BDE和△DCF中,
∴△BDE≌△DCF(AAS),
(2)∵△BDE≌△DCF,
∴DE=CF,
∵DE∥CF,
∴四边形DEFC是平行四边形,
∴EF∥BC.
22、证明:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°;
(2)∠1=∠2,
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,
∴∠1=∠2.
同步练习
一.选择题(共12小题)
1.如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达A和B的点C,分别延长AC,BC到D,E,使CD=CA,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是( )
A.SSS
B.ASA
C.AAS
D.SAS
2.下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,AB=DE
D.∠B=∠E,∠C=∠F,AC=DF
3.如图,已知∠ABC=∠DCB,添加以下条件,不能使△ABC≌△DCB的是( )
A.AB=DC
B.∠A=∠D
C.AC=DB
D.∠ACB=∠DBC
4.如图,AE∥FD,AE=DF,要使△EAB≌△FDC,需要添加的条件可以是( )
A.AB=BC
B.EB=FC
C.∠A=∠F
D.AB=CD
5.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E
B.AC=DF
C.∠ACD=∠BFE
D.BF=CD
6.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=6cm,OC=4cm,则OB的长为( )
A.2cm
B.3cm
C.4cm
D.6cm
7.如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:其中正确的结论有( )
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A.2个
B.3个
C.4个
D.5个
8.如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF;③BD=CE.两两组合在一起,共有三种组合:
(1)①②(2)①③(3)②③问能判定AB=AC的组合的是( )
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(1)(2)(3)
9.如图,线段AB与CD相交于点O,AO=BO,CO=DO,BC⊥CD,若BC=6,AC=10,则CD的长为( )
A.6
B.7
C.8
D.9
10.如图,已知AB=CD且AB⊥CD,连接AD,分别过点C,B作CE⊥AD,BF⊥AD,垂足分别为E,F.若AD=10,CE=8,BF=6,则EF的长为( )
A.4
B.3.5
C.3
D.2.5
11.已知:如图,AD是△ABC的中线,∠1=2∠2,CE⊥AD,BF⊥AD,点E、F为垂足,EF=6cm,则BC的长为( )
A.6cm
B.12cm
C.18cm
D.24cm
12.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
二.填空题(共5小题)
13.在△ABC中,AB=AC,∠ABC=∠ACB,CE是高,且∠ECA=36°,平面内有一异于点A,B,C,E的点D,若△ABC≌△CDA,则∠DAE的度数为
.
14.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为
m.
15.如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
16.如图,EB交AC于点M,交C于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有
.(填序号)
17.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
三.解答题(共5小题)
18.如图,A、C、D三点共线,△ABC和△CDE落在AD的同侧,AC=CE,∠B=∠BCE=∠CDE.求证:AB=CD.
19.如图AB=AD,AC=AE,∠BAE=∠DAC.
求证:(1)∠C=∠E;
(2)AM=AN.
20.如图,点A,F,D,C在同一直线上,BC,EF交于点M,∠B=∠E=90°,AF=CD,AB=DE.
求证:(1)Rt△ABC≌Rt△DEF;(2)MF=MC.
21.如图,AD为△ABC的中线,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF.
(1)求证;DE⊥DF;(2)求证:△BDE≌△DCF;(3)求证:EF∥BC.
22.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
参考答案
1-5:DDCDD
6-10:ACCCA
11-12:BD
13、117°、27°、72°和81°
14、4
:AB=ED
,①③④.
4
18、:∵∠BCD=∠A+∠B=∠BCE+∠DCE,∠B=∠BCE,
∴∠A=∠ECD,
在△ABC和△CDE中,
∴△ABC≌△CDE(AAS),
∴AB=CD.
19、:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS),
∴∠C=∠E;
(2)∵△ABC≌△ADE,
∴∠B=∠D,
在△ABM和△ADN中,
∴△ABM≌△ADN(ASA),
∴AM=AN.
20、(1)证明:∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF,
∵∠B=∠E=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL);
(2)证明:由(1)知,Rt△ABC≌Rt△DEF,
∴∠BCA=∠EFD,
∴∠MCF=∠MFC,
∴MF=MC.
21、:(1)∵DE平分∠ADB,DF平分∠ADC,
∴∠PDE=∠ADB,∠FDP=∠ADC,
∴∠EDF=∠PDE+∠PDF=∠ADB+∠ADC=(∠ADB+∠ADC)=90°,
∴DE⊥DF;
(2)∵BE⊥DE,DF⊥CF,
∴∠BED=∠DFC=90°,
∵∠BDE+∠CDF=90°,∠CDF+∠DCF=90°,
∴∠BDE=∠DCF,
∴DE∥CF,
∵D是BC中点,
∴BD=DC,
在△BDE和△DCF中,
∴△BDE≌△DCF(AAS),
(2)∵△BDE≌△DCF,
∴DE=CF,
∵DE∥CF,
∴四边形DEFC是平行四边形,
∴EF∥BC.
22、证明:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°;
(2)∠1=∠2,
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,
∴∠1=∠2.
