人教版数学八年级上册11.3 多边形及其内角和习题课件(24张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3 多边形及其内角和习题课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 368.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
三角形的内角和与外角和
习题课
导入启趣,连旧带新
1.三角形的内角和等于
.
2.直角三角形的两个锐角
.
互余
3.三角形的外角由三角形内角的一条
和另一边的
组成.
边
反向延长线
三角形共有
个外角;每个顶点处有
个外角,它们是
角.
六
两
对顶
1800
4.三角形外角的性质
(1)三角形的一个外角等于与它
的
两个内角的和;
(2)三角形的一个外角大于任何一个与它
的内角。
不相邻
不相邻
(3)三角形的一个外角与它相邻的内角
;
互补
(4).三角形的外角和等于
360
0
.
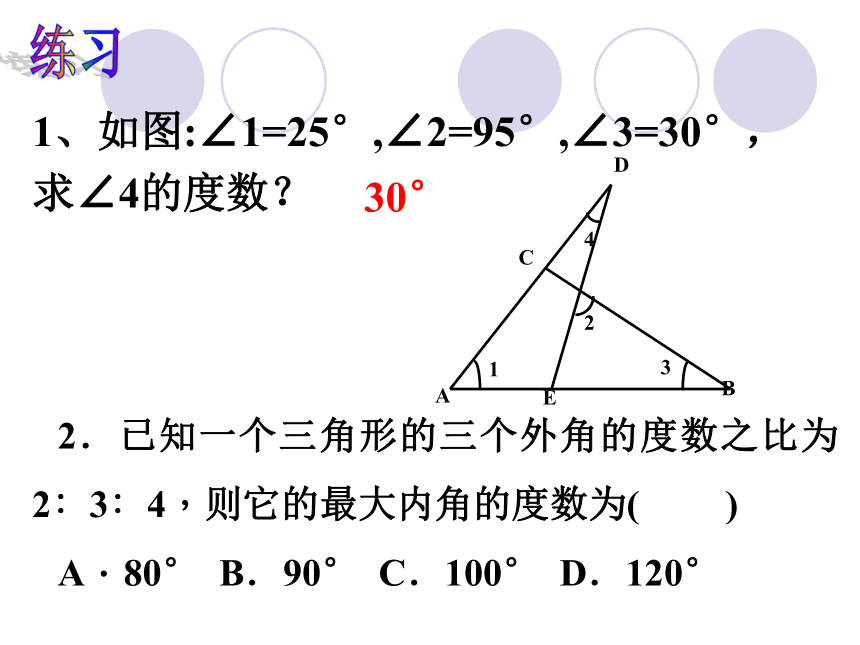
1、如图:∠1=25°,∠2=95°,∠3=30°,求∠4的度数?
A
D
E
C
B
1
4
3
2
30°
练习
2.已知一个三角形的三个外角的度数之比为2∶3∶4,则它的最大内角的度数为(
)
A.80°
B.90°
C.100°
D.120°
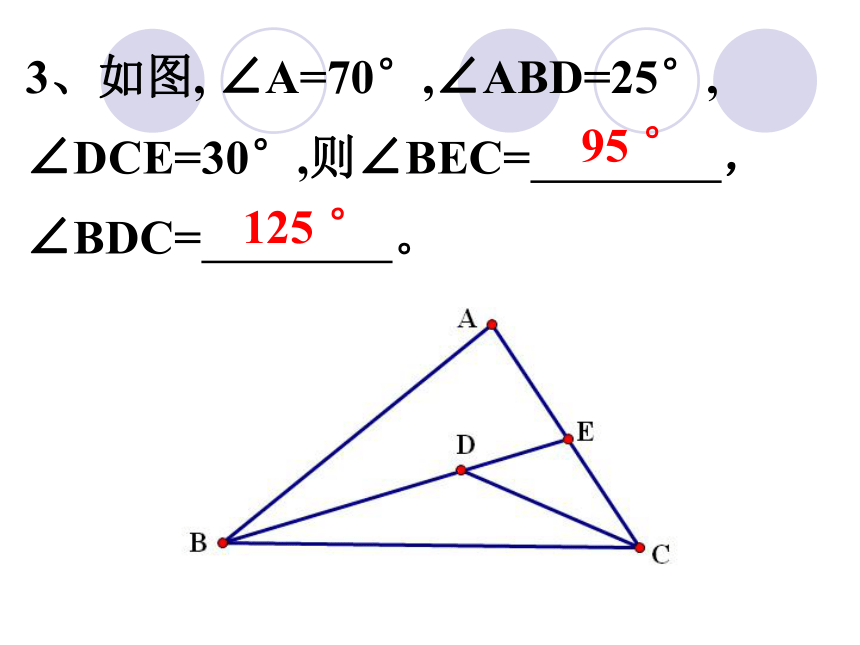
3、如图,
∠A=70°,∠ABD=25°,
∠DCE=30°,则∠BEC=
,
∠BDC=
。
95
°
125
°
4.如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )
A.35°
B.45°
C.55°
D.65°
C
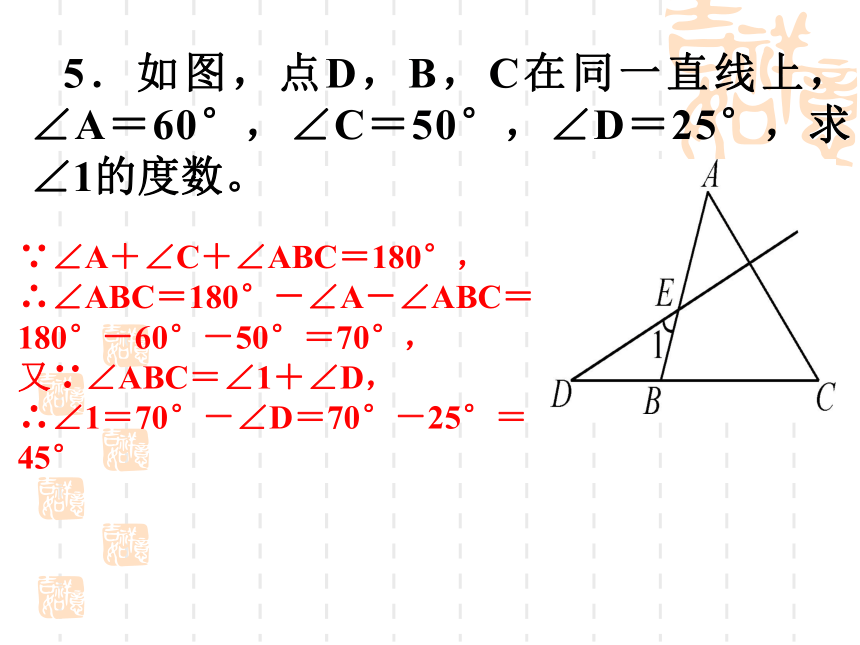
5.如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=25°,求∠1的度数。
∵∠A+∠C+∠ABC=180°,
∴∠ABC=180°-∠A-∠ABC=180°-60°-50°=70°,
又∵∠ABC=∠1+∠D,
∴∠1=70°-∠D=70°-25°=45°
6.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向.C处在B处的北偏东80°方向,则∠ACB等于( )
A.40°
B.75°
C.85°
D.140°
C
例1.
如图所示,在△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数。
解:
∠CAB=180°-∠C-∠B
=180°-45°-65°
=70°
∵AE是∠BAC的角平分线,
∴∠BAE=
又∵在△ABC中,∠DAB=180°-∠ADB-∠B
=180°-90°-65°=25°
∴∠DAE=∠BAE-∠DAB=35°-25°=10°
AD是BC边上的高,
∴
∠ADB=
90°
例2
如图,
∠A=510,
∠B=200,
∠C=300,
计算∠BOC.
例
如图,
∠A=510,
∠B=200,
∠C=300,
计算∠BOC.
D
101°
例
如图,
∠A=510,
∠B=200,
∠C=300,
计算∠BOC.
101°
F
例3、如图,五角星五个角∠A,∠B,∠C,∠D,∠E的和是多少度?
解:
∠AFG是△FBD的外角,
∴
∠AFG=
∠B+∠D
∠AGF是△GEC的外角,
∴
∠AGF=
∠C+∠E
又∵∠AGF+
∠AFG+
∠A=
180
?
,
∴
∠A+∠B+∠C+∠D+∠E
=
180
?
小结:怎样计算类似图形的角度的和?
利用三角形的内角和与外角的知识,
将其中几个角转化为某个三角形(图
形)内部,再利用内角和知识来解答.
A
B
E
C
D
活学活用,拓展延伸
如下几个图形是五角星和它的变形.
(1)把五角星中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D
+∠E)有无变化说明你的结论的正确性.?
A
B
C
D
E
变式2
(2)把五角星中的点C向上移到BD上时,如图所示,五个角的和(即∠CAD+∠B+
∠ACE+∠D+∠E)有无变化说明你的结论的正确性.
例4.如图,已知△ABC中,AD是△ABC外角∠EAC的平分线,且交BC的延长线于点D,你能比较∠ACB与∠B的大小吗?说出你的理由.
∠ACB>∠B.
∵∠ACB>∠1,AD平分∠CAE,
∴∠1=∠2,
∴∠ACB>∠2,
又∵∠2>∠B,
∴∠ACB>∠B
1.如图所示,AD、AE分别是△ABC的角平分线和高,若∠B=50°,∠C=70°,求∠DAE和∠BAD的度数.
10°,
30°
作业:
2、如图,
BC⊥AD,
垂足是D.若∠A=210,
∠B=420,求∠C,
∠BFD,
∠AEB的度数。
B
D
┐
F
E
A
C
69
°,
48°,
111
°
3.如图所示,
△ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
130
°
4、
△ABC中,
BE为∠ABC的平分线,
CE为∠ACD的平分线,
两线交于E点.你能找出∠E与∠A有什么关系吗?
E
D
C
B
A
例4.(1)△ABC中∠ABC与∠ACB的平分线相交于点P.试探索∠BPC与∠A的数量关系.
1
2
解:
(2)点P是△ABC中顶点B、C处外角平分线的交点。试探索∠BPC与∠A的大小关系。
1
2
解:
(3)点P是△ABC中内角∠ABC平分线与外角∠ACD平分线的交点.试探索∠BPC与∠A的大小关系.
1
2
解:
三角形的内角和与外角和
习题课
导入启趣,连旧带新
1.三角形的内角和等于
.
2.直角三角形的两个锐角
.
互余
3.三角形的外角由三角形内角的一条
和另一边的
组成.
边
反向延长线
三角形共有
个外角;每个顶点处有
个外角,它们是
角.
六
两
对顶
1800
4.三角形外角的性质
(1)三角形的一个外角等于与它
的
两个内角的和;
(2)三角形的一个外角大于任何一个与它
的内角。
不相邻
不相邻
(3)三角形的一个外角与它相邻的内角
;
互补
(4).三角形的外角和等于
360
0
.
1、如图:∠1=25°,∠2=95°,∠3=30°,求∠4的度数?
A
D
E
C
B
1
4
3
2
30°
练习
2.已知一个三角形的三个外角的度数之比为2∶3∶4,则它的最大内角的度数为(
)
A.80°
B.90°
C.100°
D.120°
3、如图,
∠A=70°,∠ABD=25°,
∠DCE=30°,则∠BEC=
,
∠BDC=
。
95
°
125
°
4.如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )
A.35°
B.45°
C.55°
D.65°
C
5.如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=25°,求∠1的度数。
∵∠A+∠C+∠ABC=180°,
∴∠ABC=180°-∠A-∠ABC=180°-60°-50°=70°,
又∵∠ABC=∠1+∠D,
∴∠1=70°-∠D=70°-25°=45°
6.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向.C处在B处的北偏东80°方向,则∠ACB等于( )
A.40°
B.75°
C.85°
D.140°
C
例1.
如图所示,在△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数。
解:
∠CAB=180°-∠C-∠B
=180°-45°-65°
=70°
∵AE是∠BAC的角平分线,
∴∠BAE=
又∵在△ABC中,∠DAB=180°-∠ADB-∠B
=180°-90°-65°=25°
∴∠DAE=∠BAE-∠DAB=35°-25°=10°
AD是BC边上的高,
∴
∠ADB=
90°
例2
如图,
∠A=510,
∠B=200,
∠C=300,
计算∠BOC.
例
如图,
∠A=510,
∠B=200,
∠C=300,
计算∠BOC.
D
101°
例
如图,
∠A=510,
∠B=200,
∠C=300,
计算∠BOC.
101°
F
例3、如图,五角星五个角∠A,∠B,∠C,∠D,∠E的和是多少度?
解:
∠AFG是△FBD的外角,
∴
∠AFG=
∠B+∠D
∠AGF是△GEC的外角,
∴
∠AGF=
∠C+∠E
又∵∠AGF+
∠AFG+
∠A=
180
?
,
∴
∠A+∠B+∠C+∠D+∠E
=
180
?
小结:怎样计算类似图形的角度的和?
利用三角形的内角和与外角的知识,
将其中几个角转化为某个三角形(图
形)内部,再利用内角和知识来解答.
A
B
E
C
D
活学活用,拓展延伸
如下几个图形是五角星和它的变形.
(1)把五角星中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D
+∠E)有无变化说明你的结论的正确性.?
A
B
C
D
E
变式2
(2)把五角星中的点C向上移到BD上时,如图所示,五个角的和(即∠CAD+∠B+
∠ACE+∠D+∠E)有无变化说明你的结论的正确性.
例4.如图,已知△ABC中,AD是△ABC外角∠EAC的平分线,且交BC的延长线于点D,你能比较∠ACB与∠B的大小吗?说出你的理由.
∠ACB>∠B.
∵∠ACB>∠1,AD平分∠CAE,
∴∠1=∠2,
∴∠ACB>∠2,
又∵∠2>∠B,
∴∠ACB>∠B
1.如图所示,AD、AE分别是△ABC的角平分线和高,若∠B=50°,∠C=70°,求∠DAE和∠BAD的度数.
10°,
30°
作业:
2、如图,
BC⊥AD,
垂足是D.若∠A=210,
∠B=420,求∠C,
∠BFD,
∠AEB的度数。
B
D
┐
F
E
A
C
69
°,
48°,
111
°
3.如图所示,
△ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
A
H
E
D
C
B
130
°
4、
△ABC中,
BE为∠ABC的平分线,
CE为∠ACD的平分线,
两线交于E点.你能找出∠E与∠A有什么关系吗?
E
D
C
B
A
例4.(1)△ABC中∠ABC与∠ACB的平分线相交于点P.试探索∠BPC与∠A的数量关系.
1
2
解:
(2)点P是△ABC中顶点B、C处外角平分线的交点。试探索∠BPC与∠A的大小关系。
1
2
解:
(3)点P是△ABC中内角∠ABC平分线与外角∠ACD平分线的交点.试探索∠BPC与∠A的大小关系.
1
2
解:
