2.6.3 有理数的加减混合运算 课件(共18张PPT)
文档属性
| 名称 | 2.6.3 有理数的加减混合运算 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1001.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 06:06:41 | ||
图片预览



文档简介
2.6 有理数的混合运算
第二章
有理数及其运算
2020年秋季北师大版七年级上册
有理数加减混合运算的步骤
(1)把算式中的减法都转化为加法;
(2)省略加号与括号;
(3)进行运算(尽可能利用运算律简化计算).
一、知识回顾
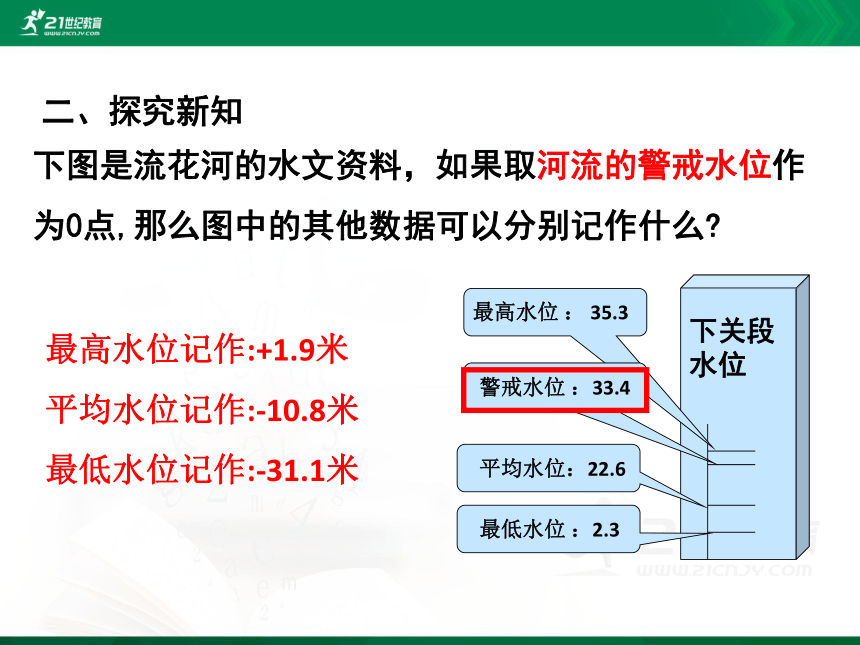
最高水位记作:+1.9米
平均水位记作:-10.8米
最低水位记作:-31.1米
下关段水位
最高水位 : 35.3
警戒水位 :33.4
平均水位:22.6
最低水位 :2.3
下图是流花河的水文资料,如果取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?
二、探究新知
下表是今年预计流花河一周的水位变化情况:(上周末的水位达到了警戒水位)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化(米)
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
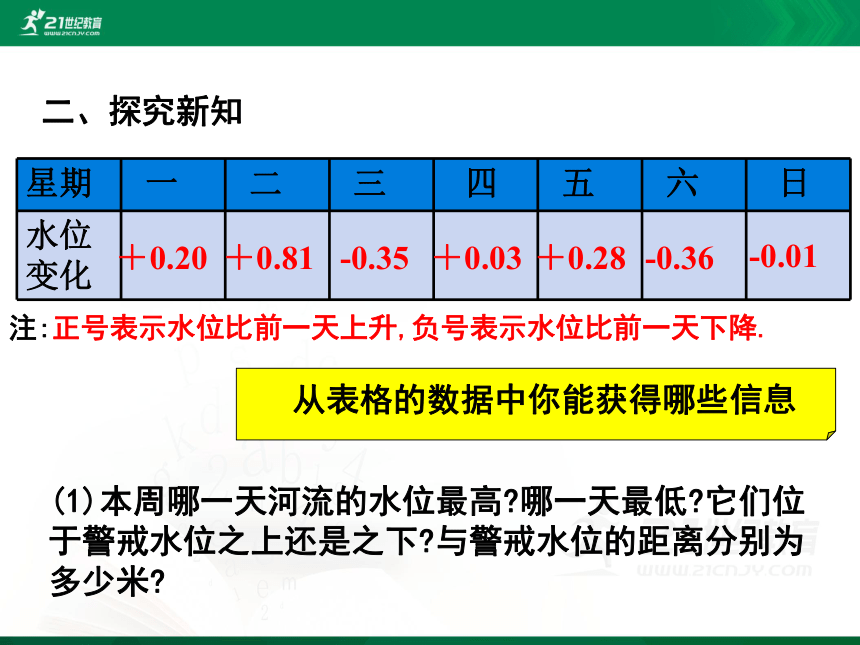
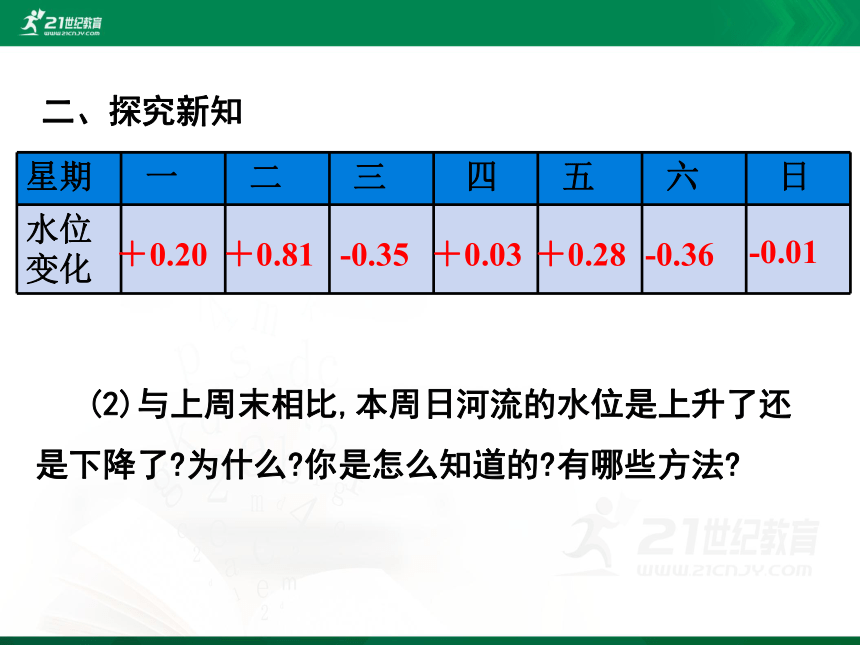
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
二、探究新知
(1)本周哪一天河流的水位最高?哪一天最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别为多少米?
从表格的数据中你能获得哪些信息
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
二、探究新知
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
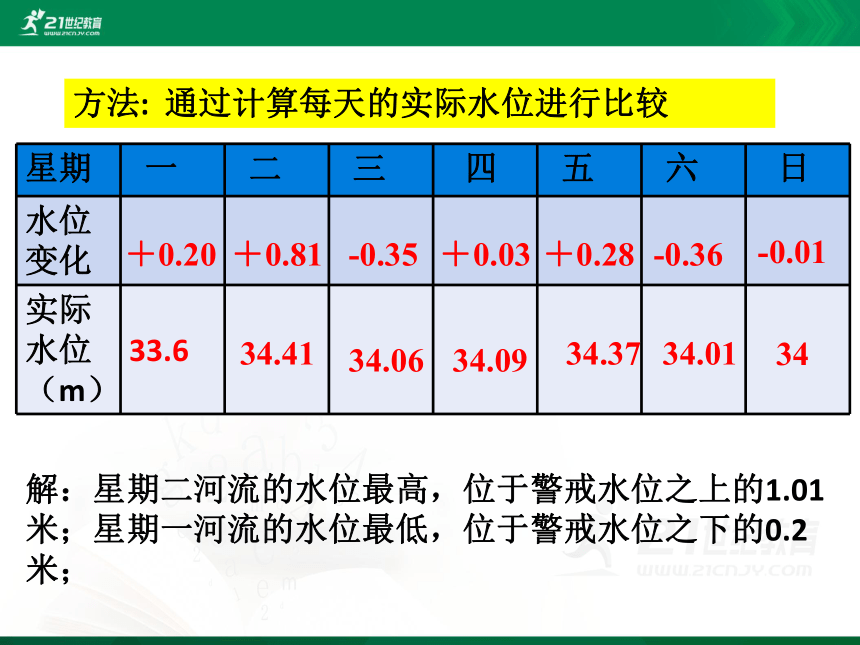
方法: 通过计算每天的实际水位进行比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
实际水位(m)
33.6
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
34.41
34.06
34.09
34.37
34.01
34
解:星期二河流的水位最高,位于警戒水位之上的1.01米;星期一河流的水位最低,位于警戒水位之下的0.2米;
(2)与上周末相比,本周日河流的水位是上升了还是下降了?为什么?你是怎么知道的?有哪些方法?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
二、探究新知
方法一: 通过计算每天的实际水位进行比较
(1)+0.2 + (+0.81) + (-0.35) + (+0.03) + (+0.28) +(-0.36) + (-0.01) = 0.60(米)
(2)0.2+0.81-0.35+0.03+0.28-0.36-0.01=0.60(米)
方法二: 对水位变化的数据求和
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
实际水位(m)
33.6
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
34.41
34.06
34.09
34.37
34.01
34
日
一
二
三
四
五
六
日
0.2
0.4
0.6
0.8
1.0
水位/米
星期
方法三: 根据变化数据画折线图
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
1. 某气象员为了掌握一周内天气的变化情况,测量了一周内的气温. 下表是一周内气温变化情况(用正数表示比前一日上升的度数,用负数表示下降的度数)
试分析经过一周,气温是上升还是下降了.
解:2+(-1)+(-2)+4+(-2.5)+1+0.5=2(℃).
答:经过一周气温上升了2 ℃.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
气温变化/℃
2
-1
-2
4
-2.5
1
0.5
三、典例讲解
2.已知上周周五(周末不开盘)收盘时股市指数以2880点报收,本周内股市涨跌情况如下表,则本周四收盘时的股市指数是多少?
解:正数表示涨,负数表示跌,每天的变化是相对于前一天来比较的,所以周四的股市指数为2880+50-21-100+78=2887.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
股指变化
+50
-21
-100
+78
-78
三、典例讲解
1. 一天早晨的气温是-7 ℃,中午上升了11 ℃,晚上又下降9 ℃,则晚上的气温是( )
A. -5 ℃ B. -6 ℃
C. -7 ℃ D. -8 ℃
A
四、课堂练习
2. 某天上午6:00虹桥水库的水位为30.4 m,到上午11:30分水位上涨了5.3 m,则下午6:00的水位下跌了0.9 m. 则下午6:00的水位为( )
A. 26 m B. 34.8 m
C. 35.8 m D. 36.6 m
B
3. 一个人在南北方向的路上行走,如果规定向北为正,这个人走了+25 m,接着走了-10 m,又走了-20 m,那么他实际上( )
A. 向北走了5 m B. 向南走了10 m
C. 向南走了5 m D. 向北走了10 m
C
4. 一个病人每天下午需要测量血压,该病人上周日的收缩压为120单位,下表是该病人这周一到周五与前一天相比较收缩压的变化情况:
本周星期二的收缩压是( )
A. 110 B. 120 C. 125 D. 130
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
增减
+20
-30
-25
+15
+30
5. 去年7月份小明到银行开户,存入1500元,以后每月根据收支情况存入一笔钱,下表为小明从 8月份到12月份的存款情况:
则截止到去年12月份,存折上共有( )
A. 9 750元 B. 8 050元
C. 1 750元 D. 9 550元
D
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月份
8
9
10
11
12
与上一月比较
-100
-200
+500
+300
-250
四、课堂练习
6. 南京出租车司机小李某一时段全是在中山东路上来回行驶,你能否知道在他将最后一位乘客送到目的地时,他距离出车的出发点有多远?
解:该出租车离出发点的距离为:
15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4+( -5)
=13千米 答:他距离出车的出发点13千米
如果规定向东为正,向西为负,我行车里程(单位:千米)为: 15, -2, 5, -1, -10, -3, -2, 12, 4, -5,
四、课堂练习
会用数学去解决生活中的变化现象,对于几次连续的变化情况可以用有理数的加减法去解决
很多实际问题可以转化为有理数的加减混合运算来解决,根据需要可以“人为”地规定零点.
我们可以借助表格和折线统计图形象直观的反映事物的变化情况
生活中处处有数学, 只要我们去观察研究
五、课堂小结
六、布置作业
课本P48习题2.9 第1、2题
谢谢
第二章
有理数及其运算
2020年秋季北师大版七年级上册
有理数加减混合运算的步骤
(1)把算式中的减法都转化为加法;
(2)省略加号与括号;
(3)进行运算(尽可能利用运算律简化计算).
一、知识回顾
最高水位记作:+1.9米
平均水位记作:-10.8米
最低水位记作:-31.1米
下关段水位
最高水位 : 35.3
警戒水位 :33.4
平均水位:22.6
最低水位 :2.3
下图是流花河的水文资料,如果取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?
二、探究新知
下表是今年预计流花河一周的水位变化情况:(上周末的水位达到了警戒水位)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化(米)
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
二、探究新知
(1)本周哪一天河流的水位最高?哪一天最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别为多少米?
从表格的数据中你能获得哪些信息
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
二、探究新知
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
方法: 通过计算每天的实际水位进行比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
实际水位(m)
33.6
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
34.41
34.06
34.09
34.37
34.01
34
解:星期二河流的水位最高,位于警戒水位之上的1.01米;星期一河流的水位最低,位于警戒水位之下的0.2米;
(2)与上周末相比,本周日河流的水位是上升了还是下降了?为什么?你是怎么知道的?有哪些方法?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
二、探究新知
方法一: 通过计算每天的实际水位进行比较
(1)+0.2 + (+0.81) + (-0.35) + (+0.03) + (+0.28) +(-0.36) + (-0.01) = 0.60(米)
(2)0.2+0.81-0.35+0.03+0.28-0.36-0.01=0.60(米)
方法二: 对水位变化的数据求和
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
实际水位(m)
33.6
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
34.41
34.06
34.09
34.37
34.01
34
日
一
二
三
四
五
六
日
0.2
0.4
0.6
0.8
1.0
水位/米
星期
方法三: 根据变化数据画折线图
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
水位变化
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
1. 某气象员为了掌握一周内天气的变化情况,测量了一周内的气温. 下表是一周内气温变化情况(用正数表示比前一日上升的度数,用负数表示下降的度数)
试分析经过一周,气温是上升还是下降了.
解:2+(-1)+(-2)+4+(-2.5)+1+0.5=2(℃).
答:经过一周气温上升了2 ℃.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
六
日
气温变化/℃
2
-1
-2
4
-2.5
1
0.5
三、典例讲解
2.已知上周周五(周末不开盘)收盘时股市指数以2880点报收,本周内股市涨跌情况如下表,则本周四收盘时的股市指数是多少?
解:正数表示涨,负数表示跌,每天的变化是相对于前一天来比较的,所以周四的股市指数为2880+50-21-100+78=2887.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
股指变化
+50
-21
-100
+78
-78
三、典例讲解
1. 一天早晨的气温是-7 ℃,中午上升了11 ℃,晚上又下降9 ℃,则晚上的气温是( )
A. -5 ℃ B. -6 ℃
C. -7 ℃ D. -8 ℃
A
四、课堂练习
2. 某天上午6:00虹桥水库的水位为30.4 m,到上午11:30分水位上涨了5.3 m,则下午6:00的水位下跌了0.9 m. 则下午6:00的水位为( )
A. 26 m B. 34.8 m
C. 35.8 m D. 36.6 m
B
3. 一个人在南北方向的路上行走,如果规定向北为正,这个人走了+25 m,接着走了-10 m,又走了-20 m,那么他实际上( )
A. 向北走了5 m B. 向南走了10 m
C. 向南走了5 m D. 向北走了10 m
C
4. 一个病人每天下午需要测量血压,该病人上周日的收缩压为120单位,下表是该病人这周一到周五与前一天相比较收缩压的变化情况:
本周星期二的收缩压是( )
A. 110 B. 120 C. 125 D. 130
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}星期
一
二
三
四
五
增减
+20
-30
-25
+15
+30
5. 去年7月份小明到银行开户,存入1500元,以后每月根据收支情况存入一笔钱,下表为小明从 8月份到12月份的存款情况:
则截止到去年12月份,存折上共有( )
A. 9 750元 B. 8 050元
C. 1 750元 D. 9 550元
D
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月份
8
9
10
11
12
与上一月比较
-100
-200
+500
+300
-250
四、课堂练习
6. 南京出租车司机小李某一时段全是在中山东路上来回行驶,你能否知道在他将最后一位乘客送到目的地时,他距离出车的出发点有多远?
解:该出租车离出发点的距离为:
15+(-2)+5+(-1)+(-10)+( -3)+( -2)+12+4+( -5)
=13千米 答:他距离出车的出发点13千米
如果规定向东为正,向西为负,我行车里程(单位:千米)为: 15, -2, 5, -1, -10, -3, -2, 12, 4, -5,
四、课堂练习
会用数学去解决生活中的变化现象,对于几次连续的变化情况可以用有理数的加减法去解决
很多实际问题可以转化为有理数的加减混合运算来解决,根据需要可以“人为”地规定零点.
我们可以借助表格和折线统计图形象直观的反映事物的变化情况
生活中处处有数学, 只要我们去观察研究
五、课堂小结
六、布置作业
课本P48习题2.9 第1、2题
谢谢
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
