北师大版八年级数学上册单元测试卷附答案:第三章 位置与坐标(Word版)
文档属性
| 名称 | 北师大版八年级数学上册单元测试卷附答案:第三章 位置与坐标(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 551.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 21:52:45 | ||
图片预览


文档简介
第三章
位置与坐标
一、选择题(共16小题;共48分)
1.
根据下列表述,能确定位置的是
A.
红星电影院
排
B.
北京市四环路
C.
北偏东
D.
东经
,北纬
2.
若点
与点
关于
轴对称,则
A.
,
B.
,
C.
,
D.
,
3.
根据下列表述,能确定位置的是
A.
国际影城
排
B.
A
市南京路口
C.
北偏东
D.
东经
,北纬
4.
如图,在平面直角坐标系中,点
的坐标为
A.
B.
C.
D.
5.
在平面直角坐标系中,点
关于
轴的对称点的坐标是
A.
B.
C.
D.
6.
由所有到已知点
的距离大于或等于
,并且小于或等于
的点组成的图形的面积为
A.
B.
C.
D.
7.
在平面直角坐标系
中,若
点坐标为
,
点坐标为
,则三角形
的面积为
A.
B.
C.
D.
8.
将
的三个顶点的横坐标乘以
,纵坐标不变,则所得图形
A.
与原图形关于
轴对称
B.
与原图形关于
轴对称
C.
与原图形关于原点对称
D.
向
轴的负方向平移了一个单位
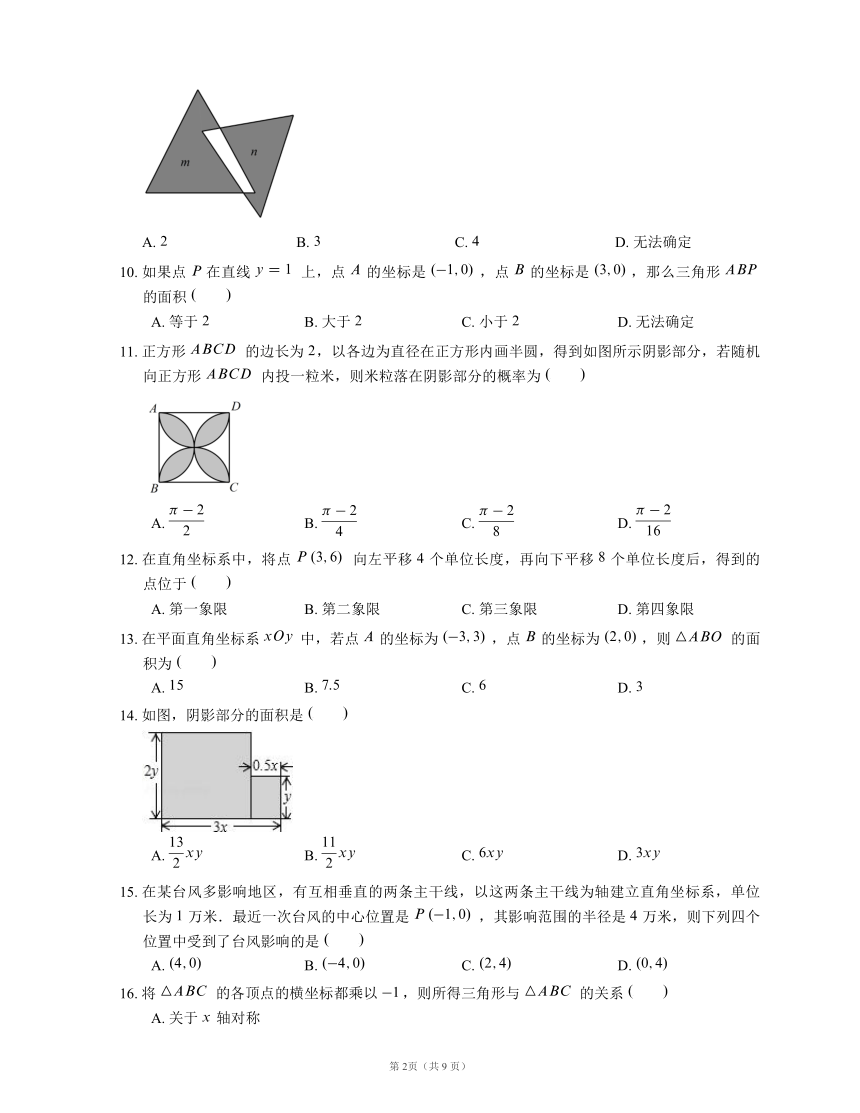
9.
如图,两个三角形的面积分别是
和
,对应阴影部分的面积分别是
,
则
等于
A.
B.
C.
D.
无法确定
10.
如果点
在直线
上,点
的坐标是
,点
的坐标是
,那么三角形
的面积
A.
等于
B.
大于
C.
小于
D.
无法确定
11.
正方形
的边长为
,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形
内投一粒米,则米粒落在阴影部分的概率为
A.
B.
C.
D.
12.
在直角坐标系中,将点
向左平移
个单位长度,再向下平移
个单位长度后,得到的点位于
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
13.
在平面直角坐标系
中,若点
的坐标为
,点
的坐标为
,则
的面积为
A.
B.
C.
D.
14.
如图,阴影部分的面积是
A.
B.
C.
D.
15.
在某台风多影响地区,有互相垂直的两条主干线,以这两条主干线为轴建立直角坐标系,单位长为
万米.最近一次台风的中心位置是
,其影响范围的半径是
万米,则下列四个位置中受到了台风影响的是
A.
B.
C.
D.
16.
将
的各顶点的横坐标都乘以
,则所得三角形与
的关系
A.
关于
轴对称
B.
关于
轴对称
C.
关于原点对称
D.
将三角形
向左平移了一个单位
二、填空题(共7小题;共35分)
17.
如果点
在直线
上,点
的坐标是
,点
的坐标是
,那么三角形
的面积为
?.
18.
如果用
表示电影院的座位号是
排
号,那么
表示
?;
排
号可表示为
?.
19.
已知点
在第二象限,且到
轴的距离是
,到
轴的距离是
,则
点的坐标为
?.
20.
如图是由边长为
和
的两个正方形组成,小颖闭上眼睛随意用针扎这个图形,小孔出现在阴影部分的概率是
?.
21.
在平面直角坐标系中,已知点
在第二象限,则点
关于直线
(直线
上各点的横坐标都是
)对称的点的坐标是
?.
22.
如图,在平面直角坐标系中,
的顶点
在
轴的正半轴上,顶点
的坐标为
,点
的坐标为
,点
为斜边
上的一动点,则
的最小值为
?.
23.
的各顶点坐标为
,,,则
的面积为
?.
三、解答题(共5小题;共67分)
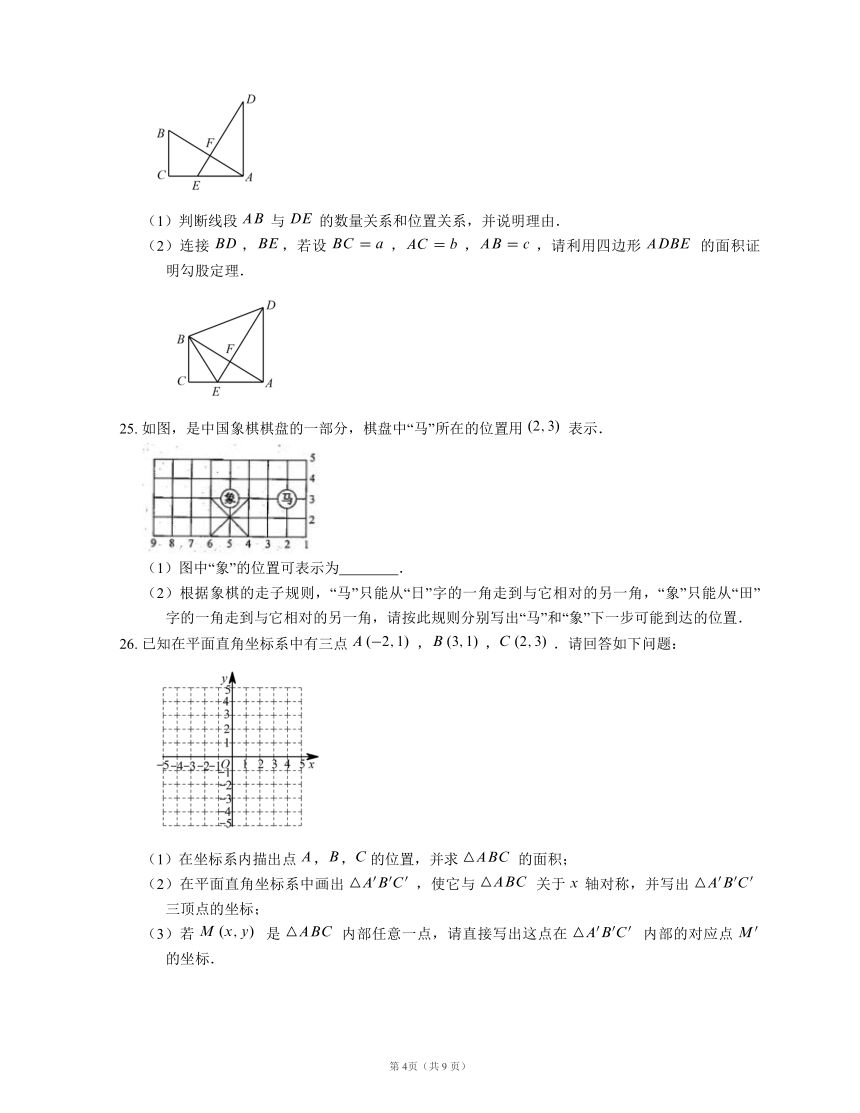
24.
如图,在
中,,
为
上一点,且
,过点
作
,垂足为
,且
,,
交于点
.
(1)判断线段
与
的数量关系和位置关系,并说明理由.
(2)连接
,,若设
,,,请利用四边形
的面积证明勾股定理.
25.
如图,是中国象棋棋盘的一部分,棋盘中“马”所在的位置用
表示.
(1)图中“象”的位置可表示为
?.
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角,“象”只能从“田”字的一角走到与它相对的另一角,请按此规则分别写出“马”和“象”下一步可能到达的位置.
26.
已知在平面直角坐标系中有三点
,,.请回答如下问题:
(1)在坐标系内描出点
,,
的位置,并求
的面积;
(2)在平面直角坐标系中画出
,使它与
关于
轴对称,并写出
三顶点的坐标;
(3)若
是
内部任意一点,请直接写出这点在
内部的对应点
的坐标.
27.
如图,在长方形
中,
为平面直角坐标系的原点,
点的坐标为
,
点的坐标为
,点
在第一象限内,点
从原点出发,以每秒
个单位的速度沿着
的路线移动(即沿着长方形移动一周).
(1)写出
点的坐标.
(2)当点
移动了
秒时,指出此时
点的位置,并写出点
的坐标.
(3)在移动过程中,当点
到
轴距离为
个单位长度时,求点
移动的时间.
28.
如图,,,点
在
轴上,且
.
(1)求点
的坐标;
(2)求
的面积;
(3)在
轴上是否存在点
,使以
,,
三点为顶点的三角形的面积为
?若存在,请直接写出点
的坐标;若不存在,请说明理由.
答案
第一部分
1.
D
2.
D
3.
D
4.
A
5.
A
6.
C
7.
D
8.
A
9.
B
10.
A
11.
A
12.
C
13.
D
14.
B
【解析】阴影部分面积为:.
15.
B
16.
B
第二部分
17.
18.
排号,
19.
20.
【解析】
图形的总面积为
,阴影部分面积为
,
小孔出现在阴影部分的概率是
.
21.
22.
23.
第三部分
24.
(1)
,,理由如下,
因为
,
所以
,
在
和
中,
所以
,
所以
,,
又因为
,
所以
,
所以
,
即
.
??????(2)
所以
,
即
.
25.
(1)
??????(2)
“马”下一步可能到达的位置:,,,,,;
“象”下一步可能到达的位置:,,,.
26.
(1)
描点如图
,
顺次连接点
,,,
由题意得,,且
,
.
??????(2)
如图
,
,,.
??????(3)
.
27.
(1)
.
??????(2)
点
在
中点处,坐标为
.
??????(3)
当点
在
上时,则
,
(秒);
当点
在
上时,则
,
(秒),
综上所述,点
移动的时间为
秒或
秒.
28.
(1)
如图,
点
在点
的右边时,,点
在点
的左边时,,
所以,
的坐标为
或
.
??????(2)
的面积
.
??????(3)
设点
到
轴的距离为
,则
,
解得
,
点
在
轴正半轴时,,
点
在
轴负半轴时,,
综上所述,点
的坐标为
或
.
第1页(共1
页)
位置与坐标
一、选择题(共16小题;共48分)
1.
根据下列表述,能确定位置的是
A.
红星电影院
排
B.
北京市四环路
C.
北偏东
D.
东经
,北纬
2.
若点
与点
关于
轴对称,则
A.
,
B.
,
C.
,
D.
,
3.
根据下列表述,能确定位置的是
A.
国际影城
排
B.
A
市南京路口
C.
北偏东
D.
东经
,北纬
4.
如图,在平面直角坐标系中,点
的坐标为
A.
B.
C.
D.
5.
在平面直角坐标系中,点
关于
轴的对称点的坐标是
A.
B.
C.
D.
6.
由所有到已知点
的距离大于或等于
,并且小于或等于
的点组成的图形的面积为
A.
B.
C.
D.
7.
在平面直角坐标系
中,若
点坐标为
,
点坐标为
,则三角形
的面积为
A.
B.
C.
D.
8.
将
的三个顶点的横坐标乘以
,纵坐标不变,则所得图形
A.
与原图形关于
轴对称
B.
与原图形关于
轴对称
C.
与原图形关于原点对称
D.
向
轴的负方向平移了一个单位
9.
如图,两个三角形的面积分别是
和
,对应阴影部分的面积分别是
,
则
等于
A.
B.
C.
D.
无法确定
10.
如果点
在直线
上,点
的坐标是
,点
的坐标是
,那么三角形
的面积
A.
等于
B.
大于
C.
小于
D.
无法确定
11.
正方形
的边长为
,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形
内投一粒米,则米粒落在阴影部分的概率为
A.
B.
C.
D.
12.
在直角坐标系中,将点
向左平移
个单位长度,再向下平移
个单位长度后,得到的点位于
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
13.
在平面直角坐标系
中,若点
的坐标为
,点
的坐标为
,则
的面积为
A.
B.
C.
D.
14.
如图,阴影部分的面积是
A.
B.
C.
D.
15.
在某台风多影响地区,有互相垂直的两条主干线,以这两条主干线为轴建立直角坐标系,单位长为
万米.最近一次台风的中心位置是
,其影响范围的半径是
万米,则下列四个位置中受到了台风影响的是
A.
B.
C.
D.
16.
将
的各顶点的横坐标都乘以
,则所得三角形与
的关系
A.
关于
轴对称
B.
关于
轴对称
C.
关于原点对称
D.
将三角形
向左平移了一个单位
二、填空题(共7小题;共35分)
17.
如果点
在直线
上,点
的坐标是
,点
的坐标是
,那么三角形
的面积为
?.
18.
如果用
表示电影院的座位号是
排
号,那么
表示
?;
排
号可表示为
?.
19.
已知点
在第二象限,且到
轴的距离是
,到
轴的距离是
,则
点的坐标为
?.
20.
如图是由边长为
和
的两个正方形组成,小颖闭上眼睛随意用针扎这个图形,小孔出现在阴影部分的概率是
?.
21.
在平面直角坐标系中,已知点
在第二象限,则点
关于直线
(直线
上各点的横坐标都是
)对称的点的坐标是
?.
22.
如图,在平面直角坐标系中,
的顶点
在
轴的正半轴上,顶点
的坐标为
,点
的坐标为
,点
为斜边
上的一动点,则
的最小值为
?.
23.
的各顶点坐标为
,,,则
的面积为
?.
三、解答题(共5小题;共67分)
24.
如图,在
中,,
为
上一点,且
,过点
作
,垂足为
,且
,,
交于点
.
(1)判断线段
与
的数量关系和位置关系,并说明理由.
(2)连接
,,若设
,,,请利用四边形
的面积证明勾股定理.
25.
如图,是中国象棋棋盘的一部分,棋盘中“马”所在的位置用
表示.
(1)图中“象”的位置可表示为
?.
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角,“象”只能从“田”字的一角走到与它相对的另一角,请按此规则分别写出“马”和“象”下一步可能到达的位置.
26.
已知在平面直角坐标系中有三点
,,.请回答如下问题:
(1)在坐标系内描出点
,,
的位置,并求
的面积;
(2)在平面直角坐标系中画出
,使它与
关于
轴对称,并写出
三顶点的坐标;
(3)若
是
内部任意一点,请直接写出这点在
内部的对应点
的坐标.
27.
如图,在长方形
中,
为平面直角坐标系的原点,
点的坐标为
,
点的坐标为
,点
在第一象限内,点
从原点出发,以每秒
个单位的速度沿着
的路线移动(即沿着长方形移动一周).
(1)写出
点的坐标.
(2)当点
移动了
秒时,指出此时
点的位置,并写出点
的坐标.
(3)在移动过程中,当点
到
轴距离为
个单位长度时,求点
移动的时间.
28.
如图,,,点
在
轴上,且
.
(1)求点
的坐标;
(2)求
的面积;
(3)在
轴上是否存在点
,使以
,,
三点为顶点的三角形的面积为
?若存在,请直接写出点
的坐标;若不存在,请说明理由.
答案
第一部分
1.
D
2.
D
3.
D
4.
A
5.
A
6.
C
7.
D
8.
A
9.
B
10.
A
11.
A
12.
C
13.
D
14.
B
【解析】阴影部分面积为:.
15.
B
16.
B
第二部分
17.
18.
排号,
19.
20.
【解析】
图形的总面积为
,阴影部分面积为
,
小孔出现在阴影部分的概率是
.
21.
22.
23.
第三部分
24.
(1)
,,理由如下,
因为
,
所以
,
在
和
中,
所以
,
所以
,,
又因为
,
所以
,
所以
,
即
.
??????(2)
所以
,
即
.
25.
(1)
??????(2)
“马”下一步可能到达的位置:,,,,,;
“象”下一步可能到达的位置:,,,.
26.
(1)
描点如图
,
顺次连接点
,,,
由题意得,,且
,
.
??????(2)
如图
,
,,.
??????(3)
.
27.
(1)
.
??????(2)
点
在
中点处,坐标为
.
??????(3)
当点
在
上时,则
,
(秒);
当点
在
上时,则
,
(秒),
综上所述,点
移动的时间为
秒或
秒.
28.
(1)
如图,
点
在点
的右边时,,点
在点
的左边时,,
所以,
的坐标为
或
.
??????(2)
的面积
.
??????(3)
设点
到
轴的距离为
,则
,
解得
,
点
在
轴正半轴时,,
点
在
轴负半轴时,,
综上所述,点
的坐标为
或
.
第1页(共1
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
