等差数列前n项和
图片预览





文档简介
(共18张PPT)
等差数列前n项和
——最值、通项
复习回顾
等差数列的性质:设数列{an}为等差数列,公差d
复习回顾
2.等差数列前n项和Sn公式:
说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。
代入an=a1+(n-1)d
教学目标
教学目标
掌握求等差数列前n项和最值问题的方法
会根据
新课探究
等差数列通项公式
从通项角度求最值
等差数列前n项和公式
从函数角度求最值
n
Sn
O
10
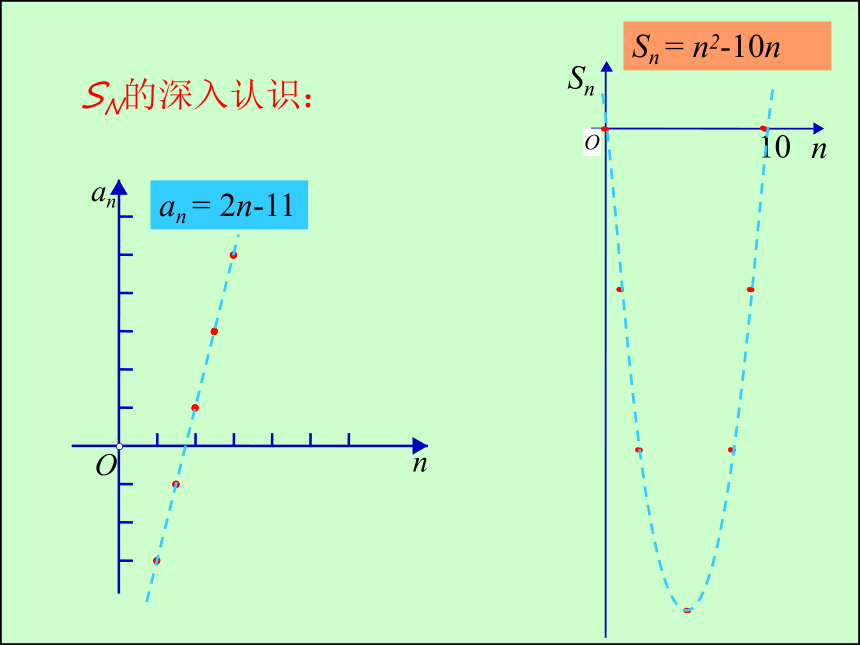
sn的深入认识:
n
an
O
an = 2n-11
Sn = n2-10n
反思公式
思考:
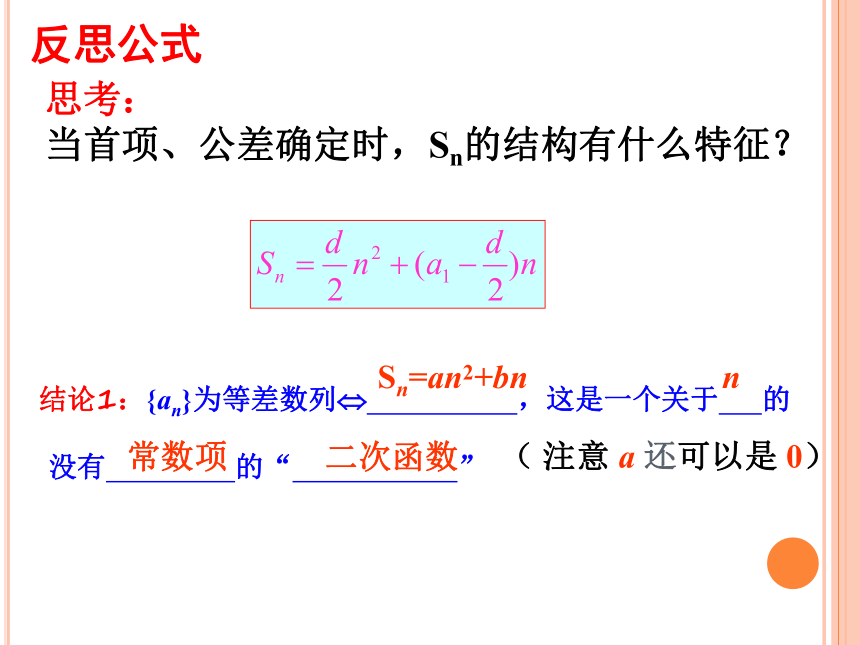
当首项、公差确定时,Sn的结构有什么特征?
结论1:{an}为等差数列 ,这是一个关于 的
没有 的“ ”
Sn=an2+bn
常数项
二次函数
( 注意 a 还可以是 0)
n
规律总结:等差数列最值
当d不为0时,可以看做关于n的二次函数。因此可以通过配方求,及此时n的值。
利用
若
若
规律总结:已知
注意:=,
所以首先的代入n=1求出,然后再用=求通项。
典例分析
例一、等差数列
1、求数列通项公式
2、数列前n项和,求的最大值及对应的n值。
思路点拨:等差数列通项公式
要求
其中
从哪一项开始小于零,那么我们就能判断出最小值项,从而进行运算
例题解析
因为
所以
解得:
所以
从哪一项开始小于零?
解不等式
得
那么很显然从12项开始小于零,特别的
解答过程
点评
典例分析
例二、数列
1、求数列的通项公式。
2、求证:数列是等差数列。
3、求该数列前n项和的最大值,并求此时对应的n值。
思路点拨: 求通项,然后求解。
Sn
n
0
16 .
17
例题解析
解:
所以可得
证明:
所以此数列是等差数列。
所以当n=16或17时最大,最大值为272
求时不要忘记验证是否符合通项公式。
注意考虑n为正整数,然后通过二次函数性质找最值
解答过程
点评
思考题
如果定义数列,其中
1、求数列前30项和
2、求数列前n项和的表达式。
思路点拨:
例题解析
解:由例二知数列前16项大于0
所以
同理可得
解答过程
反馈练习
反馈小结答案
1、C
2、A
3、前三项
4、
5、不是,
谢谢指导
等差数列前n项和
——最值、通项
复习回顾
等差数列的性质:设数列{an}为等差数列,公差d
复习回顾
2.等差数列前n项和Sn公式:
说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。
代入an=a1+(n-1)d
教学目标
教学目标
掌握求等差数列前n项和最值问题的方法
会根据
新课探究
等差数列通项公式
从通项角度求最值
等差数列前n项和公式
从函数角度求最值
n
Sn
O
10
sn的深入认识:
n
an
O
an = 2n-11
Sn = n2-10n
反思公式
思考:
当首项、公差确定时,Sn的结构有什么特征?
结论1:{an}为等差数列 ,这是一个关于 的
没有 的“ ”
Sn=an2+bn
常数项
二次函数
( 注意 a 还可以是 0)
n
规律总结:等差数列最值
当d不为0时,可以看做关于n的二次函数。因此可以通过配方求,及此时n的值。
利用
若
若
规律总结:已知
注意:=,
所以首先的代入n=1求出,然后再用=求通项。
典例分析
例一、等差数列
1、求数列通项公式
2、数列前n项和,求的最大值及对应的n值。
思路点拨:等差数列通项公式
要求
其中
从哪一项开始小于零,那么我们就能判断出最小值项,从而进行运算
例题解析
因为
所以
解得:
所以
从哪一项开始小于零?
解不等式
得
那么很显然从12项开始小于零,特别的
解答过程
点评
典例分析
例二、数列
1、求数列的通项公式。
2、求证:数列是等差数列。
3、求该数列前n项和的最大值,并求此时对应的n值。
思路点拨: 求通项,然后求解。
Sn
n
0
16 .
17
例题解析
解:
所以可得
证明:
所以此数列是等差数列。
所以当n=16或17时最大,最大值为272
求时不要忘记验证是否符合通项公式。
注意考虑n为正整数,然后通过二次函数性质找最值
解答过程
点评
思考题
如果定义数列,其中
1、求数列前30项和
2、求数列前n项和的表达式。
思路点拨:
例题解析
解:由例二知数列前16项大于0
所以
同理可得
解答过程
反馈练习
反馈小结答案
1、C
2、A
3、前三项
4、
5、不是,
谢谢指导
