5.1极差

(共16张PPT)
沭阳县杨岗寄宿学校 章杰兵
初中数学九年级上册
（苏科版）
2.1极差
1. 经历刻画数据离散程度的探索过程，感受
表示数据离散程度的必要性．
2.掌握极差的概念，理解其统计意义，并
在具体情境中加以应用．
学习目标:
学习重点:极差的计算方法及其意义．
学习难点:培养学生思维能力和观察能力，
发展统计意识．
1.活动一：请看课本第41页，然后回答下面三个问题．
（1）请分别算出甲、乙两名跳高运动员的近8次成绩的平均数．
（2）这两名运动员的比赛成绩名有什么特点？
（3）如果你是教练员，会派哪位运动员去参赛呢？
自主探究
自主合作
2．活动二：请看课本第42页，
（1）你认为哪个厂生产的乒乓球的直径与
标准的误差更小呢 说出你的理由
（2）在这个情境中，能否根据平均数、众数
或中位数来比较哪个厂生产质量好？
自主合作
2．活动二：请看课本第42页，
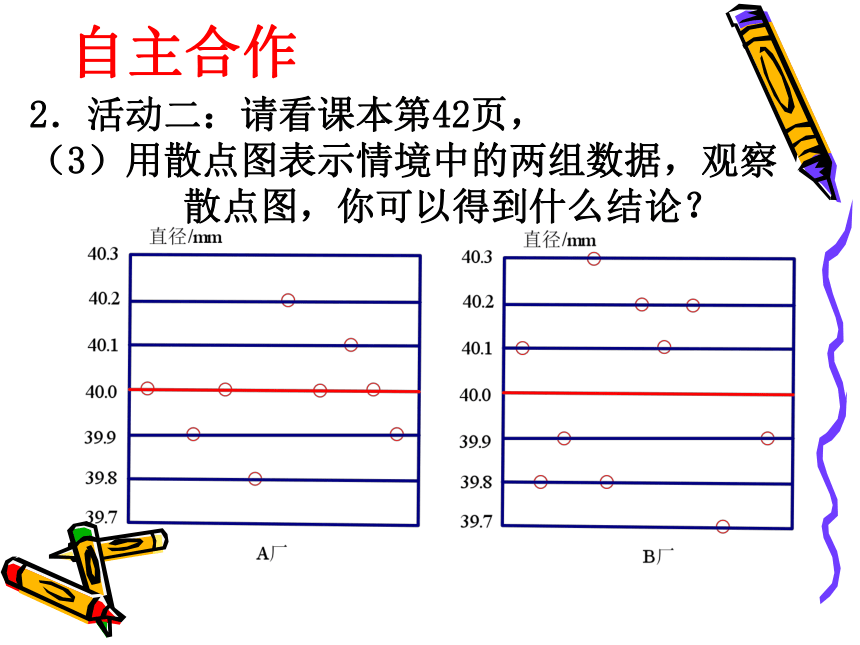
（3）用散点图表示情境中的两组数据，观察
散点图，你可以得到什么结论？
在生活中，我们常常会和极差打交道.篮球队里个子最高的队员比个子最矮的队员高多少？家庭中年纪最大的长辈比年纪最小的孩子大多少？一家公司成员中最高收入与最低收入相比.这些都是求极差的例子.
3.什么样的指标可以反映一组数据变化范围的大小？
极差＝最大值－最小值．
极差:一组数据中的最大数据与最小数据的差
极差能够反映数据的变化范围.极差是最简单的一种度量数据波动情况的量,但它受极端值的影响较大.
你能举一些关于极差的例子吗
请分别算出活动一与活动二中两组数据的极差．
自主合作
活动一：
甲:1.60,1.55,1.58,1.59,1.62,1.63,1.58,1.57；
乙:1.50,1.631.62,1.51,1.52,1.61,1.60,1.65．
请分别算出活动一与活动二中两组数据的极差．
自主合作
活动二：
A厂：40.0，40.1，39.9，40.0，39.8，
40.2，40.0，40.1，40.0，39.9；
B厂：40.1，39.8，39.9，40.3，39.8，
40.2，40.1，40.2，39.7 ，39.9 .
自主展示
活动三：自学课本第43页例题，然后完成下列问题：
（1）完成课本第43页练习1、2、3.
（2）某日在不同时段测得乌鲁木齐和广州的气温情况如下表所示：
0：00 4：00 8：00 12：00 16：00 20：00
乌鲁木齐 -2 。C -1 。C 8。C 10。C 9。C 2 。C
广 州 20 。C 22 。C 23 。C 25 。C 23 。C 21 。C
自主展示
活动三：
（2）某日在不同时段测得乌鲁木齐和广州的气温情况如下表所示：
0：00 4：00 8：00 12：00 16：00 20：00
乌鲁木齐 -2 。C -1 。C 8。C 10。C 9。C 2 。C
广 州 20 。C 22 。C 23 。C 25 。C 23 。C 21 。C
根据上表回答：分别计算乌鲁木齐、广州当天的温度极差是多少？如果你有两个好朋友分别要去这两个地方旅游你将给他们分别提出什么建议？
10-（-2）=12℃
25-20=5℃
自主拓展
为什么说两个城市，
一个“四季如春”，一个“四季分明”？
这里四季分明。
这里四季如春
自主拓展
2．（1）3，4，2，1，5的极差是 ；
（2）若一组数据的最小值为12，极差
为20，则这组数据的最大值为 ；
（3）若一组数据的最大值为12，极差
为 20，则这组数据的最小值为 ．
4
32
-8
3．a+3，a+4，a+2，a+1，a+5的
平均数为 ，中位数为 ， 极差为 ．
自主拓展
4
a+3
a+3
观察下图，分别说出两段时间内气温的极差．
解：由图可知，图(a)中极差为16℃；
　　　　　　　图(b)中极差为7℃．
5．北京时间2008年8月17日消息，北京奥运会男子50米步枪3×40决赛举行．美国选手埃蒙斯在倒数第二轮领先将近4环的情况下，最后一轮仅打出了4.4环，中国选手邱健凭借最后一枪稳定的发挥以总成绩1272.5环获得了金．埃蒙斯以总成绩1270.3环仅获第四．根据最后10成绩，分别算出他们最后10轮成绩的极差，并用所学知识谈谈自己的看法．
1 2 3 4 5 6 7 8 9 10
邱健 10.2 8.8 10.5 10.6 9.3 9.4 10 10.3 10.4 10
埃蒙斯 9.7 10.2 10.5 10.1 10.5 10 10.1 10 9.8 4.4
（单位：环）
五、自主评价
1.本节课你学到了哪些知识？
2.本节课中你最大的收获是什么？