湘教版数学九年级下册1.2.3 y=ax2+bx+c的图象与性质教学课件(共31张PPT)
文档属性
| 名称 | 湘教版数学九年级下册1.2.3 y=ax2+bx+c的图象与性质教学课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
二次函数的图像和性质
教学课件
湘教版九年级下册
01
新课导入
新课导入
2018年世界杯足球赛在俄罗斯举行,你观看比赛了么?一个足球被从地面向上踢出,它距地面高度h(m)可以用二次函数h=-4.9t2+19.6t表示,其中t(s)表示足球被踢出后经过的时间,那么你知道经过多长时间,足球到达它的最高点?最高点的高度是多少呢?你知道怎样计算么?
02
新知探究
新知探究
一.将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k
问题1:如何画出
的图象呢?
我们已经会画
y=a(x-h)2+k
的图象,因此,只需要把配方成的形式就可以了.
新知探究
配方法
提取二次项系数
配方
整理
化简:去掉中括号
一.将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k
新知探究
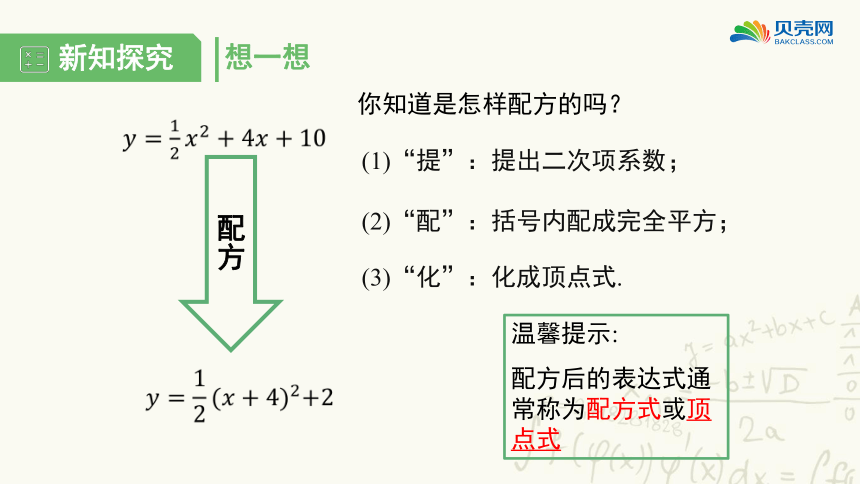
想一想
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
温馨提示:
配方后的表达式通常称为配方式或顶点式
新知探究
我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x-h)2+k?
y=ax?+bx+c
=
=
=
=
一.将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k
新知探究
归纳总结
一般地,二次函数y=ax2+bx+c的可以通过配方化成y=a(x-h)2+k的形式,即
顶点坐标是(-,
),对称轴是
因此,当时,
函数达到最大值(<0)或最小值>0):
新知探究
练一练
已知二次函数
有下列说法:
其图象的开口向下;
其图象的对称轴为直线x=-3;
其图象的顶点坐标为(3,-1);
当x<3时,y随着x的增大而缩小。
其中说法正确的有(
)
A.1个
B.2个
C.3个
D.4个
A
思路引导:
用配方法把化为顶点式为
,
根据函数的性质对各方法分析判断。
2
新知探究
归纳总结
用配方法把一般式化为顶点式的步骤:
(1)提取二次项系数,将括号内的二次项系数化为1;
(2)将提取后括号内的式子配方;
(3)利用分配律将上式化为顶点式。
新知探究
二.二次函数
y=ax2+bx+c
的图象与性质
根据顶点式确定对称轴,顶点坐标.
x
…
-4
-3
-2
-1
…
…
…
列表:自变量x从顶点的横坐标-4开始取值.
对称轴:直线x=-4;顶点坐标:(-4,2).
2
4
6.5
我们已经知道那么现在你会画这个二次函数的图象吗?
新知探究
画一画
描点、连线,画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分,即得.
O
x
1
-1
●
●
●
●
●
(-4,2)
●
●
3
5
7
-3
-5
-7
新知探究
想一想
从图看出,当x等于多少时,函数的值最小?这个最小值是多少?
当x等于顶点的横坐标-4时,函数值最小,这个最小值等于顶点的纵坐标2.
这个函数的增减性是怎样的?
当x<-4时,函数值随x的增大而
减小;当x>-4时,函数值随x的
增大而增大.
O
x
1
-1
●
●
●
●
●
(-4,2)
●
●
3
5
7
-3
-5
-7
新知探究
练一练
求下列函数的最大值或最小值:
(1)
(2)
思路引导:
1、二次函数y=a(x-h)2+k,当a
0时,函数有最小值,y最小值=
2、二次函数y=ax2+bx+c,当a
0时,函数有最大值,y最大值=
>
k
<
函数有最小值,值为
-
函数有最大值,值为
新知探究
练一练
解:(1)
=2(
)
=2(
+
)
=2
∵a=2>0,∴函数有最小值,最小值为。
(2)
∵a=-1,b=-3,c=4
∴=
∵a=-1<0,∴函数有最大值,最大值为。
新知探究
归纳总结a>0
(1)
x
y
O
如果a>0,当x<
时,y随x的增大而减小;当x
>
时,y随x的增大而增大;当x=
时,函数达到最小值,最小值为
.
二.二次函数
y=ax2+bx+c
的图象与性质
x=-
-
-
-
新知探究
归纳总结a<0
(2)
x
y
O
如果a<0,当x<
时,y随x的增大而增大;当x>
时,y随x的增大而减小;当x=
时,函数达到最大值,最大值为
.
二.二次函数
y=ax2+bx+c
的图象与性质
-
-
-
x=-
新知探究
练一练
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=
-9a;④若(-3,y1),(
,y2)是抛物线上两点,则y1>y2.
其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.②③④
x
y
O
2
x=-1
B
解析:对称轴=-1,∴
,所以①正确;
图像过(2,0),∴
所以③正确;根据点与对称轴距离可知y1>y2,
所以④正确。
03
典型例题
典型例题
1.若抛物线y=-x2+bx+c经过点(-2,3),则2c-4b+9的值是(
).
A.5
B.-1
C.4
D.18
A
典型例题
2.下列对二次函数y=x2-x的图象的描述,正确的是(
).
C
A.开口向下
B.对称轴是y轴
C.经过原点
D.在对称轴右侧的部分是下降的
典型例题
3.已知二次函数y=x2-(m-1)x+(m+1)的图象经过点(2,0)。
(1)求m的值;
(2)求此二次函数的顶点坐标。
解:(1)
∵二次函数y=x2-(m-1)x+(m+1)的图象经过点(2,0),
∴
22-2(m-1)+(m+1)=0,
解得m=7.
(2)由(1)可知m=7,
∴此二次函数的解析式为y=x2-6x+8=
∴二次函数的顶点坐标为(3,-1).
m=7
顶点坐标为(3,-1)
04
拓展提高
拓展提高
已知二次函数y
=-.
(1)在给定的直角坐标系中,画出这个函数图象;
(2)根据图象,写出当y<0时x的取值范围;
(3)若将此图象沿x轴向右平移3个单位长度,请写出平移后图象所对应的函数关系式。
x<-3或x>1
y=-+2
拓展提高
解:
(1)二次函数的横纵坐标为
x=-=-1,y==2,
当x=0时,y=,
当y=0时,x=1或x=-3.
图象如图所示。
(2)据图可知,当y<0时,x<-3或x>1.
(3)
∵y
=-=-+2,
∴若将此图象沿x轴向右平移3个单位长度,平移后的图象所对应的函数关系式为y=-+2.
05
课堂小结
课堂小结
06
作业布置
1、巩固本节所学的所有有关二次函数的图像与性质
2、完成课本习题
1.2
A、B组
作业布置
谢
谢
观
看
二次函数的图像和性质
教学课件
湘教版九年级下册
01
新课导入
新课导入
2018年世界杯足球赛在俄罗斯举行,你观看比赛了么?一个足球被从地面向上踢出,它距地面高度h(m)可以用二次函数h=-4.9t2+19.6t表示,其中t(s)表示足球被踢出后经过的时间,那么你知道经过多长时间,足球到达它的最高点?最高点的高度是多少呢?你知道怎样计算么?
02
新知探究
新知探究
一.将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k
问题1:如何画出
的图象呢?
我们已经会画
y=a(x-h)2+k
的图象,因此,只需要把配方成的形式就可以了.
新知探究
配方法
提取二次项系数
配方
整理
化简:去掉中括号
一.将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k
新知探究
想一想
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
温馨提示:
配方后的表达式通常称为配方式或顶点式
新知探究
我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x-h)2+k?
y=ax?+bx+c
=
=
=
=
一.将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k
新知探究
归纳总结
一般地,二次函数y=ax2+bx+c的可以通过配方化成y=a(x-h)2+k的形式,即
顶点坐标是(-,
),对称轴是
因此,当时,
函数达到最大值(<0)或最小值>0):
新知探究
练一练
已知二次函数
有下列说法:
其图象的开口向下;
其图象的对称轴为直线x=-3;
其图象的顶点坐标为(3,-1);
当x<3时,y随着x的增大而缩小。
其中说法正确的有(
)
A.1个
B.2个
C.3个
D.4个
A
思路引导:
用配方法把化为顶点式为
,
根据函数的性质对各方法分析判断。
2
新知探究
归纳总结
用配方法把一般式化为顶点式的步骤:
(1)提取二次项系数,将括号内的二次项系数化为1;
(2)将提取后括号内的式子配方;
(3)利用分配律将上式化为顶点式。
新知探究
二.二次函数
y=ax2+bx+c
的图象与性质
根据顶点式确定对称轴,顶点坐标.
x
…
-4
-3
-2
-1
…
…
…
列表:自变量x从顶点的横坐标-4开始取值.
对称轴:直线x=-4;顶点坐标:(-4,2).
2
4
6.5
我们已经知道那么现在你会画这个二次函数的图象吗?
新知探究
画一画
描点、连线,画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分,即得.
O
x
1
-1
●
●
●
●
●
(-4,2)
●
●
3
5
7
-3
-5
-7
新知探究
想一想
从图看出,当x等于多少时,函数的值最小?这个最小值是多少?
当x等于顶点的横坐标-4时,函数值最小,这个最小值等于顶点的纵坐标2.
这个函数的增减性是怎样的?
当x<-4时,函数值随x的增大而
减小;当x>-4时,函数值随x的
增大而增大.
O
x
1
-1
●
●
●
●
●
(-4,2)
●
●
3
5
7
-3
-5
-7
新知探究
练一练
求下列函数的最大值或最小值:
(1)
(2)
思路引导:
1、二次函数y=a(x-h)2+k,当a
0时,函数有最小值,y最小值=
2、二次函数y=ax2+bx+c,当a
0时,函数有最大值,y最大值=
>
k
<
函数有最小值,值为
-
函数有最大值,值为
新知探究
练一练
解:(1)
=2(
)
=2(
+
)
=2
∵a=2>0,∴函数有最小值,最小值为。
(2)
∵a=-1,b=-3,c=4
∴=
∵a=-1<0,∴函数有最大值,最大值为。
新知探究
归纳总结a>0
(1)
x
y
O
如果a>0,当x<
时,y随x的增大而减小;当x
>
时,y随x的增大而增大;当x=
时,函数达到最小值,最小值为
.
二.二次函数
y=ax2+bx+c
的图象与性质
x=-
-
-
-
新知探究
归纳总结a<0
(2)
x
y
O
如果a<0,当x<
时,y随x的增大而增大;当x>
时,y随x的增大而减小;当x=
时,函数达到最大值,最大值为
.
二.二次函数
y=ax2+bx+c
的图象与性质
-
-
-
x=-
新知探究
练一练
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=
-9a;④若(-3,y1),(
,y2)是抛物线上两点,则y1>y2.
其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.②③④
x
y
O
2
x=-1
B
解析:对称轴=-1,∴
,所以①正确;
图像过(2,0),∴
所以③正确;根据点与对称轴距离可知y1>y2,
所以④正确。
03
典型例题
典型例题
1.若抛物线y=-x2+bx+c经过点(-2,3),则2c-4b+9的值是(
).
A.5
B.-1
C.4
D.18
A
典型例题
2.下列对二次函数y=x2-x的图象的描述,正确的是(
).
C
A.开口向下
B.对称轴是y轴
C.经过原点
D.在对称轴右侧的部分是下降的
典型例题
3.已知二次函数y=x2-(m-1)x+(m+1)的图象经过点(2,0)。
(1)求m的值;
(2)求此二次函数的顶点坐标。
解:(1)
∵二次函数y=x2-(m-1)x+(m+1)的图象经过点(2,0),
∴
22-2(m-1)+(m+1)=0,
解得m=7.
(2)由(1)可知m=7,
∴此二次函数的解析式为y=x2-6x+8=
∴二次函数的顶点坐标为(3,-1).
m=7
顶点坐标为(3,-1)
04
拓展提高
拓展提高
已知二次函数y
=-.
(1)在给定的直角坐标系中,画出这个函数图象;
(2)根据图象,写出当y<0时x的取值范围;
(3)若将此图象沿x轴向右平移3个单位长度,请写出平移后图象所对应的函数关系式。
x<-3或x>1
y=-+2
拓展提高
解:
(1)二次函数的横纵坐标为
x=-=-1,y==2,
当x=0时,y=,
当y=0时,x=1或x=-3.
图象如图所示。
(2)据图可知,当y<0时,x<-3或x>1.
(3)
∵y
=-=-+2,
∴若将此图象沿x轴向右平移3个单位长度,平移后的图象所对应的函数关系式为y=-+2.
05
课堂小结
课堂小结
06
作业布置
1、巩固本节所学的所有有关二次函数的图像与性质
2、完成课本习题
1.2
A、B组
作业布置
谢
谢
观
看
