2020-2021学年数学人教B版(2019)选择性必修第一册:第一章 空间向量与立体几何 质量检测(含答案解析)
文档属性
| 名称 | 2020-2021学年数学人教B版(2019)选择性必修第一册:第一章 空间向量与立体几何 质量检测(含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 470.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览




文档简介
章末质量检测(一) 空间向量与立体几何
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.以下四组向量:①a=(1,-2,1),b=(-1,2,-1);②a=(8,4,0),b=(2,1,0);③a=(1,0,-1),b=(-3,0,3);④a=,b=(4,-3,3).其中互相平行的是( )
A.②③ B.①④
C.①②④ D.①②③④
2.已知向量a=(2,-3,5)与b=(4,x,y)平行,则x,y的值为( )
A.6和-10 B.-6和10
C.-6和-10 D.6和10
3.在四面体O?ABC中,点P为棱BC的中点.设=a,=b,=c,那么向量用基底{a,b,c}可表示为( )
A.-a+b+c B.-a+b+c
C.a+b+c D.a+b+c
4.正方体ABCD?A1B1C1D1中,BB1与平面ACD1所成角的余弦值为( )
A. B. C. D.
5.已知长方体ABCD?A1B1C1D1,下列向量的数量积一定不为0的是( )
A.AD1·B1C
B.BD1·
C.·AD1
D.BD1·
6.已知A(-4,6,-1),B(4,3,2),则下列各向量中是平面AOB的一个法向量的是( )
A.(0,1,6) B.(-1,2,-1)
C.(-15,4,36) D.(15,4,-36)
7.四棱锥P?ABCD中,底面ABCD是平行四边形,=(2,-1,-4),=(4,2,0),=(-1,2,-1),则PA与底面ABCD的关系是( )
A.相交 B.垂直 C.不垂直 D.成60°角
8.已知正四棱锥S?ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE与平面SBC所成的角的余弦值为( )
A. B. C. D.
9.如图所示,在四面体PABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B?AP?C的余弦值为( )
A. B.
C. D.
10.已知四边形ABCD是边长为4的正方形,E,F分别是边AB,AD的中点,GC垂直于正方形ABCD所在平面,且GC=2,则点B到平面EFG的距离为( )
A.3 B. C. D.
11.已知四棱锥O-ABCD中,=a,=b,=c,点M在OA上,且OM=2MA,N为BC中点,则=( )
A.a-b+c B.a+b-c
C.-a+b+c D.a+b-c
12.将正方形ABCD沿对角线BD折成一个直二面角,点C到达点C1,则异面直线AB与C1D所成角是( )
A.90° B.60° C.45° D.30°
二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中的横线上)
13.若a=(2,-3,5),b=(-3,1,-4),则|a-2b|=__________.
14.在空间直角坐标系中,已知a=(2,-1,3),b=(-4,2,x).若a⊥b,则x=________.
15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{,,}为基底,则=________.
16.已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成角的正弦值为________.
三、解答题(本大题共6个小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(10分)在四棱锥P?ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.
(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)求异面直线AE与CD所成角的余弦值.
18.(12分)如图,在四棱锥P?ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F?AB?P的余弦值.
19.(12分)如图,在三棱锥P?ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求二面角A ? PB ? E的大小.
20.(12分)如图,已知四棱锥P ? ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P?DC?B的大小;
(3)求证:平面PAD⊥平面PAB.
21.(12分)如图,在四棱锥P?ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.
(1)求证:CD⊥平面PAD;
(2)求二面角F?AE?P的余弦值;
(3)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.
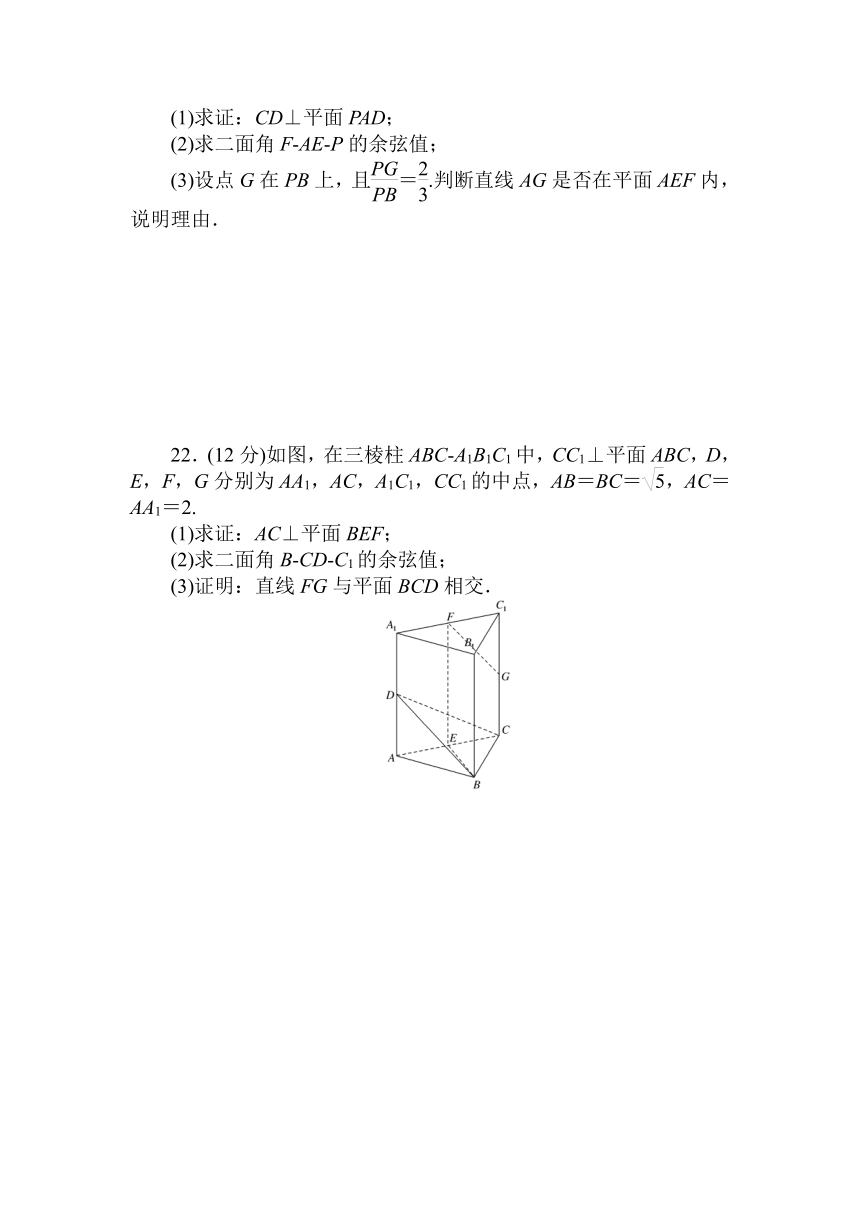
22.(12分)如图,在三棱柱ABC?A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,CC1的中点,AB=BC=,AC=AA1=2.
(1)求证:AC⊥平面BEF;
(2)求二面角B?CD?C1的余弦值;
(3)证明:直线FG与平面BCD相交.
章末质量检测(一) 空间向量与立体几何
1.解析:因为①a=(1,-2,1)=-b=-(-1,2,-1),
所以a∥b;
②a=(8,4,0),b=(2,1,0),a=4b,
所以a∥b;
③a=(1,0,-1),b=(-3,0,3),a=-b,
所以a∥b;
④a=,b=(4,-3,3),a=-b,
所以a∥b,因此选D.
答案:D
2.解析:因为向量a=(2,-3,5)与b=(4,x,y)平行,
所以解得x=-6,y=10.
答案:B
3.解析:由向量减法的三角形法则可知=-,因为P为棱BC的中点,由向量加法的平行四边形法则可知=(+),所以=-=(+)-=-a+b+c.故B正确.
答案:B
4.
解析:不妨设正方体的棱长为1,如图,建立空间直角坐标系,
则D(0,0,0),B(1,1,0),B1(1,1,1).
平面ACD1的法向量为DB1=(1,1,1),
又BB1=(0,0,1),
则cos〈DB1,BB1〉===.故BB1与平面ACD1所成角的余弦值为 =.
答案:D
5.解析:当长方体的侧面AA1D1D与BB1C1C为正方形时,AD1⊥B1C,所以AD1·B1C=0;当长方体的底面为正方形时,BD1⊥,所以BD1·=0;由长方体的性质知AB⊥平面AA1D1D,所以⊥AD1,所以·AD1=0;无论长方体具体何种结构,都不可能有BD1⊥,也就不可能有BD1·=0,故选D.
答案:D
6.解析:设法向量为(x,y,z),则
解得
令y=4,则得法向量为(15,4,-36).
答案:D
7.解析:∵·=0,·=0,
∴PA⊥AB,PA⊥AD.
又AB∩AD=A,∴PA⊥平面ABCD.
答案:B
8.解析:
设AE与平面SBC所成的角为θ,以底面中心O为原点,以射线OA为x轴正半轴,以射线OB为y轴正半轴,以射线OS为z轴正半轴,建立空间直角坐标系,设底面边长为,则A(1,0,0),B(0,1,0),C(-1,0,0),S(0,0,1),E,所以=(-1,-1,0),=(0,1,-1),=,设平面SBC的法向量为n=(x,y,z),
则即令x=1,
所以n=(1,-1,-1).
因为cos==,
所以cos θ=.故选B.
答案:B
9.解析:
如图所示,作BD⊥AP于D,作CE⊥AP于E.
设AB=1,
则易得CE=,EP=,
PA=PB=,可以求得BD=,
ED=.
因为=++,
所以2=2+2+2+2·+2·+2·,所以·=-,
所以cos〈,〉=-,由图知,二面角B?AP?C的余弦值为.故选C.
答案:C
10.解析:
如图,建立空间直角坐标系,
则B(0,4,0),E(2,4,0),F(4,2,0),G(0,0,2),=(2,4,-2),=(4,2,-2),
设n=(x,y,z)是平面EFG的一个法向量,
则
即
令x=1,则y=1,z=3,
则n=(1,1,3),而=(-2,0,0),
故d==.
答案:D
11.解析:=++
=+(-)+(-)
=-++
=-a+b+c.
答案:C
12.
解析:方法一:如图,则AB∥CD,所以C1D与CD所成的角即为异面直线AB与C1D所成角,设正方形边长为2,则OC=OC1=,所以CC1=2,所以△CC1D为等边三角形,故异面直线AB与C1D所成角是60°.
方法二:设正方形边长为2,则OA=OB=OC=OD=OC1=,建立如图所示的空间直角坐标系,则A(0,-,0),B(,0,0),C1(0,0,),D(-,0,0).
所以=(,,0),DC1=(,0,),
所以cos〈,〉===,
故异面直线AB与C1D所成角是60°.
答案:B
13.解析:∵a-2b=(8,-5,13),
∴|a-2b|==.
答案:
14.解析:因为a⊥b,所以a·b=2×(-4)+(-1)×2+3x=0,解得x=.
答案:
15.解析:连接AE,则=-
=+-
=+-(+)
=+---
=--+.
答案:--+
16.解析:如图,建立空间直角坐标系,=(0,1,0),AD1=(-1,0,1),=.
设平面ABC1D1的法向量为n=(x,y,z),
由可解得n=(1,0,1).
设直线AE与平面ABC1D1所成的角为θ,则sin θ==.
答案:
17.解析:(1)证明:∵PA⊥平面ABCD,∴PA⊥AB.
又AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,
∴AB⊥PD.
又∵AE⊥PD,AB∩AE=A,∴PD⊥平面ABE,故BE⊥PD.
(2)以A为原点,AB,AD,AP所在直线为坐标轴,建立空间直角坐标系,则点C,D的坐标分别为(a,a,0),(0,2a,0).
∵PA⊥平面ABCD,∠PDA是PD与底面ABCD所成的角,∴∠PDA=30°.
于是,在Rt△AED中,由AD=2a,得AE=a.
过E作EF⊥AD,垂足为F,在Rt△AFE中,由AE=a,∠EAF=60°,得AF=,EF=a,
∴E.
于是,=,=(-a,a,0).
设与的夹角为θ,则由cos θ===.
AE与CD所成角的余弦值为.
18.解析:
依题意,以点A为原点建立空间直角坐标系(如图),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
由E为棱PC的中点,得E(1,1,1).
(1)证明:向量=(0,1,1),=(2,0,0),
故·=0,
所以BE⊥DC.
(2)向量=(-1,2,0),=(1,0,-2).
设n=(x,y,z)为平面PBD的法向量,
则
即
不妨令y=1,可得n=(2,1,1)为平面PBD的一个法向量.
于是有cos〈n,〉===.
所以,直线BE与平面PBD所成角的正弦值为.
(3)向量=(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,
设=λ,0≤λ≤1.
故=+=+λ=(1-2λ,2-2λ,2λ).
由BF⊥AC,得·=0,
因此,2(1-2λ)+2(2-2λ)=0,解得λ=.
即=.
设n1=(x,y,z)为平面FAB的法向量,
则
即
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
取平面ABP的法向量n2=(0,1,0).
则cos〈n1,n2〉===-.
易知,二面角F?AB?P是锐角,
所以其余弦值为.
19.解析:(1)证明:D,E分别为AB,AC中点,
∴DE∥BC.
又DE?平面PBC,BC?平面PBC,
∴DE∥平面PBC.
(2)证明:连接PD,∵PA=PB,D为AB中点,
∴PD⊥AB.
∵DE∥BC,BC⊥AB,
∴DE⊥AB.
又PD∩DE=D,PD?平面PDE,DE?平面PDE,
∴AB⊥平面PDE,又PE?平面PDE,∴AB⊥PE.
(3)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,
∴PD⊥平面ABC.
如图,以D为原点建立空间直角坐标系,
∴B(1,0,0),P(0,0,),E,
∴=(1,0,-),=.
设平面PBE的法向量n1=(x,y,z),
∴
令z=,得n1=(3,2,).
∵DE⊥平面PAB,
∴平面PAB的法向量为n2=(0,1,0).
设二面角A?PB?E的大小为θ,
由图知,cos θ=|cos〈n1,n2〉|==,θ=60°,
∴二面角A?PB?E的大小为60°.
20.解析:解法一:(1)证明:∵PB=PC,∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,∴PO⊥平面ABCD.
在梯形ABCD中,可得Rt△ABO≌Rt△BCD,
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,即AO⊥BD.
∵PA在平面ABCD内的射影为AO,∴PA⊥BD.
(2)∵DC⊥BC,且平面PBC⊥平面ABCD,
∴DC⊥平面PBC.
∵PC?平面PBC,∴DC⊥PC,
∴∠PCB为二面角P?DC?B的平面角.
∵△PBC是等边三角形,∴∠PCB=60°,即二面角P?DC?B的大小为60°.
(3)证明:取PB的中点N,连接CN.
∵PC=BC,∴CN⊥PB,①
∵AB⊥BC,且平面PBC⊥平面ABCD,
∴AB⊥平面PBC.
∵AB?平面PAB,
∴平面PBC⊥平面PAB.②
由①,②知CN⊥平面PAB.
取PA的中点M,连接DM,MN,则由MN∥AB∥CD,
MN=AB=CD,得四边形MNCD为平行四边形,
∴CN∥DM,∴DM⊥平面PAB.
∵DM?平面PAD,∴平面PAD⊥平面PAB.
解法二:取BC的中点O,因为△PBC是等边三角形,由侧面PBC⊥底面ABCD,得PO⊥底面ABCD.
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O?xyz.
(1)证明:∵CD=1,∴在直角梯形中,AB=BC=2,
在等边三角形PBC中,PO=,
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,),
∴=(-2,-1,0),=(1,-2,-),
∵·=(-2)×1+(-1)×(-2)+0×(-)=0,
∴⊥,即PA⊥BD.
(2)取PC中点N,则=.
∵=(0,2,0),=(1,0,),
∴·=×0+0×2+×0=0,
·=×1+0×0+×=0,
∴⊥平面PDC,显然=(0,0,),且⊥平面ABCD,
∴,的夹角等于所求二面角的平面角.
∵·=×0+0×0+×=,||=,||=,
∴cos〈,〉==,
∴二面角P?DC?B的大小为60°.
(3)证明:取PA的中点M,连接DM,
则M的坐标为.
又=,=(1,0,-),
∴·=×1+0×(-2)+×(-)=0,
·=×1+0×0+×(-)=0,
∴⊥,⊥,
即DM⊥PA,DM⊥PB.
又∵PA∩PB=P,
∴DM⊥平面PAB,
∴平面PAD⊥平面PAB.
21.解析:(1)由于PA⊥平面ABCD,CD?平面ABCD,则PA⊥CD,
由题意可知AD⊥CD,且PA∩AD=A,
由线面垂直的判定定理可得CD⊥平面PAD.
(2)以点A为坐标原点,平面ABCD内与AD垂直的直线为x轴,AD,AP方向为y轴,z轴建立如图所示的空间直角坐标系A?xyz,
易知:A(0,0,0),P(0,0,2),C(2,2,0),D(0,2,0),
由=可得点F的坐标为F,则=,
由=可得E(0,1,1),则=(0,1,1),
设平面AEF的法向量为:m=(x,y,z),则
据此可得平面AEF的一个法向量为:m=(1,1,-1),
很明显平面AEP的一个法向量为n=(1,0,0),
cos〈m,n〉===,
二面角F?AE?P的平面角为锐角,故二面角F?AE?P的余弦值为.
(3)易知P(0,0,2),B(2,-1,0),由=可得G,
则=,
由(2)知平面AEF的一个法向量为:m=(1,1,-1),
又m·=0且点A在平面AEF内,故直线AG在平面AEF内.
22.解析:(1)在三棱柱ABC?A1B1C1中,
∵CC1⊥平面ABC,
∴四边形A1ACC1为矩形.
又E,F分别为AC,A1C1的中点,
∴AC⊥EF.
∵AB=BC.
∴AC⊥BE,又EF∩BE=E,EF?平面BEF,BE?平面BEF,
∴AC⊥平面BEF.
(2)由(1)知AC⊥EF,AC⊥BE,EF∥CC1.
又CC1⊥平面ABC,∴EF⊥平面ABC.
∵BE?平面ABC,∴EF⊥BE.
如图建立空间直角坐标系E?xyz.
由题意得B(0,2,0),C(-1,0,0),D(1,0,1),F(0,0,2),G(0,2,1).
∴=(2,0,1),=(1,2,0),
设平面BCD的法向量为n=(a,b,c),
∴,∴,
令a=2,则b=-1,c=-4,
∴平面BCD的法向量n=(2,-1,-4),
又∵平面CDC1的法向量为=(0,2,0),
∴cos〈n·〉==-.
由图可得二面角B?CD?C1为钝角,所以二面角B?CD?C1的余弦值为-.
(3)由(2)知平面BCD的法向量为n=(2,-1,-4),∵G(0,2,1),F(0,0,2),
∴=(0,-2,1),∴n·=-2,∴n与不垂直,
∴GF与平面BCD不平行且不在平面BCD内,∴GF与平面BCD相交.
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.以下四组向量:①a=(1,-2,1),b=(-1,2,-1);②a=(8,4,0),b=(2,1,0);③a=(1,0,-1),b=(-3,0,3);④a=,b=(4,-3,3).其中互相平行的是( )
A.②③ B.①④
C.①②④ D.①②③④
2.已知向量a=(2,-3,5)与b=(4,x,y)平行,则x,y的值为( )
A.6和-10 B.-6和10
C.-6和-10 D.6和10
3.在四面体O?ABC中,点P为棱BC的中点.设=a,=b,=c,那么向量用基底{a,b,c}可表示为( )
A.-a+b+c B.-a+b+c
C.a+b+c D.a+b+c
4.正方体ABCD?A1B1C1D1中,BB1与平面ACD1所成角的余弦值为( )
A. B. C. D.
5.已知长方体ABCD?A1B1C1D1,下列向量的数量积一定不为0的是( )
A.AD1·B1C
B.BD1·
C.·AD1
D.BD1·
6.已知A(-4,6,-1),B(4,3,2),则下列各向量中是平面AOB的一个法向量的是( )
A.(0,1,6) B.(-1,2,-1)
C.(-15,4,36) D.(15,4,-36)
7.四棱锥P?ABCD中,底面ABCD是平行四边形,=(2,-1,-4),=(4,2,0),=(-1,2,-1),则PA与底面ABCD的关系是( )
A.相交 B.垂直 C.不垂直 D.成60°角
8.已知正四棱锥S?ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE与平面SBC所成的角的余弦值为( )
A. B. C. D.
9.如图所示,在四面体PABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B?AP?C的余弦值为( )
A. B.
C. D.
10.已知四边形ABCD是边长为4的正方形,E,F分别是边AB,AD的中点,GC垂直于正方形ABCD所在平面,且GC=2,则点B到平面EFG的距离为( )
A.3 B. C. D.
11.已知四棱锥O-ABCD中,=a,=b,=c,点M在OA上,且OM=2MA,N为BC中点,则=( )
A.a-b+c B.a+b-c
C.-a+b+c D.a+b-c
12.将正方形ABCD沿对角线BD折成一个直二面角,点C到达点C1,则异面直线AB与C1D所成角是( )
A.90° B.60° C.45° D.30°
二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中的横线上)
13.若a=(2,-3,5),b=(-3,1,-4),则|a-2b|=__________.
14.在空间直角坐标系中,已知a=(2,-1,3),b=(-4,2,x).若a⊥b,则x=________.
15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{,,}为基底,则=________.
16.已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成角的正弦值为________.
三、解答题(本大题共6个小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(10分)在四棱锥P?ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.
(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)求异面直线AE与CD所成角的余弦值.
18.(12分)如图,在四棱锥P?ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F?AB?P的余弦值.
19.(12分)如图,在三棱锥P?ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求二面角A ? PB ? E的大小.
20.(12分)如图,已知四棱锥P ? ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P?DC?B的大小;
(3)求证:平面PAD⊥平面PAB.
21.(12分)如图,在四棱锥P?ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.
(1)求证:CD⊥平面PAD;
(2)求二面角F?AE?P的余弦值;
(3)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.
22.(12分)如图,在三棱柱ABC?A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,CC1的中点,AB=BC=,AC=AA1=2.
(1)求证:AC⊥平面BEF;
(2)求二面角B?CD?C1的余弦值;
(3)证明:直线FG与平面BCD相交.
章末质量检测(一) 空间向量与立体几何
1.解析:因为①a=(1,-2,1)=-b=-(-1,2,-1),
所以a∥b;
②a=(8,4,0),b=(2,1,0),a=4b,
所以a∥b;
③a=(1,0,-1),b=(-3,0,3),a=-b,
所以a∥b;
④a=,b=(4,-3,3),a=-b,
所以a∥b,因此选D.
答案:D
2.解析:因为向量a=(2,-3,5)与b=(4,x,y)平行,
所以解得x=-6,y=10.
答案:B
3.解析:由向量减法的三角形法则可知=-,因为P为棱BC的中点,由向量加法的平行四边形法则可知=(+),所以=-=(+)-=-a+b+c.故B正确.
答案:B
4.
解析:不妨设正方体的棱长为1,如图,建立空间直角坐标系,
则D(0,0,0),B(1,1,0),B1(1,1,1).
平面ACD1的法向量为DB1=(1,1,1),
又BB1=(0,0,1),
则cos〈DB1,BB1〉===.故BB1与平面ACD1所成角的余弦值为 =.
答案:D
5.解析:当长方体的侧面AA1D1D与BB1C1C为正方形时,AD1⊥B1C,所以AD1·B1C=0;当长方体的底面为正方形时,BD1⊥,所以BD1·=0;由长方体的性质知AB⊥平面AA1D1D,所以⊥AD1,所以·AD1=0;无论长方体具体何种结构,都不可能有BD1⊥,也就不可能有BD1·=0,故选D.
答案:D
6.解析:设法向量为(x,y,z),则
解得
令y=4,则得法向量为(15,4,-36).
答案:D
7.解析:∵·=0,·=0,
∴PA⊥AB,PA⊥AD.
又AB∩AD=A,∴PA⊥平面ABCD.
答案:B
8.解析:
设AE与平面SBC所成的角为θ,以底面中心O为原点,以射线OA为x轴正半轴,以射线OB为y轴正半轴,以射线OS为z轴正半轴,建立空间直角坐标系,设底面边长为,则A(1,0,0),B(0,1,0),C(-1,0,0),S(0,0,1),E,所以=(-1,-1,0),=(0,1,-1),=,设平面SBC的法向量为n=(x,y,z),
则即令x=1,
所以n=(1,-1,-1).
因为cos==,
所以cos θ=.故选B.
答案:B
9.解析:
如图所示,作BD⊥AP于D,作CE⊥AP于E.
设AB=1,
则易得CE=,EP=,
PA=PB=,可以求得BD=,
ED=.
因为=++,
所以2=2+2+2+2·+2·+2·,所以·=-,
所以cos〈,〉=-,由图知,二面角B?AP?C的余弦值为.故选C.
答案:C
10.解析:
如图,建立空间直角坐标系,
则B(0,4,0),E(2,4,0),F(4,2,0),G(0,0,2),=(2,4,-2),=(4,2,-2),
设n=(x,y,z)是平面EFG的一个法向量,
则
即
令x=1,则y=1,z=3,
则n=(1,1,3),而=(-2,0,0),
故d==.
答案:D
11.解析:=++
=+(-)+(-)
=-++
=-a+b+c.
答案:C
12.
解析:方法一:如图,则AB∥CD,所以C1D与CD所成的角即为异面直线AB与C1D所成角,设正方形边长为2,则OC=OC1=,所以CC1=2,所以△CC1D为等边三角形,故异面直线AB与C1D所成角是60°.
方法二:设正方形边长为2,则OA=OB=OC=OD=OC1=,建立如图所示的空间直角坐标系,则A(0,-,0),B(,0,0),C1(0,0,),D(-,0,0).
所以=(,,0),DC1=(,0,),
所以cos〈,〉===,
故异面直线AB与C1D所成角是60°.
答案:B
13.解析:∵a-2b=(8,-5,13),
∴|a-2b|==.
答案:
14.解析:因为a⊥b,所以a·b=2×(-4)+(-1)×2+3x=0,解得x=.
答案:
15.解析:连接AE,则=-
=+-
=+-(+)
=+---
=--+.
答案:--+
16.解析:如图,建立空间直角坐标系,=(0,1,0),AD1=(-1,0,1),=.
设平面ABC1D1的法向量为n=(x,y,z),
由可解得n=(1,0,1).
设直线AE与平面ABC1D1所成的角为θ,则sin θ==.
答案:
17.解析:(1)证明:∵PA⊥平面ABCD,∴PA⊥AB.
又AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,
∴AB⊥PD.
又∵AE⊥PD,AB∩AE=A,∴PD⊥平面ABE,故BE⊥PD.
(2)以A为原点,AB,AD,AP所在直线为坐标轴,建立空间直角坐标系,则点C,D的坐标分别为(a,a,0),(0,2a,0).
∵PA⊥平面ABCD,∠PDA是PD与底面ABCD所成的角,∴∠PDA=30°.
于是,在Rt△AED中,由AD=2a,得AE=a.
过E作EF⊥AD,垂足为F,在Rt△AFE中,由AE=a,∠EAF=60°,得AF=,EF=a,
∴E.
于是,=,=(-a,a,0).
设与的夹角为θ,则由cos θ===.
AE与CD所成角的余弦值为.
18.解析:
依题意,以点A为原点建立空间直角坐标系(如图),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
由E为棱PC的中点,得E(1,1,1).
(1)证明:向量=(0,1,1),=(2,0,0),
故·=0,
所以BE⊥DC.
(2)向量=(-1,2,0),=(1,0,-2).
设n=(x,y,z)为平面PBD的法向量,
则
即
不妨令y=1,可得n=(2,1,1)为平面PBD的一个法向量.
于是有cos〈n,〉===.
所以,直线BE与平面PBD所成角的正弦值为.
(3)向量=(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,
设=λ,0≤λ≤1.
故=+=+λ=(1-2λ,2-2λ,2λ).
由BF⊥AC,得·=0,
因此,2(1-2λ)+2(2-2λ)=0,解得λ=.
即=.
设n1=(x,y,z)为平面FAB的法向量,
则
即
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
取平面ABP的法向量n2=(0,1,0).
则cos〈n1,n2〉===-.
易知,二面角F?AB?P是锐角,
所以其余弦值为.
19.解析:(1)证明:D,E分别为AB,AC中点,
∴DE∥BC.
又DE?平面PBC,BC?平面PBC,
∴DE∥平面PBC.
(2)证明:连接PD,∵PA=PB,D为AB中点,
∴PD⊥AB.
∵DE∥BC,BC⊥AB,
∴DE⊥AB.
又PD∩DE=D,PD?平面PDE,DE?平面PDE,
∴AB⊥平面PDE,又PE?平面PDE,∴AB⊥PE.
(3)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,
∴PD⊥平面ABC.
如图,以D为原点建立空间直角坐标系,
∴B(1,0,0),P(0,0,),E,
∴=(1,0,-),=.
设平面PBE的法向量n1=(x,y,z),
∴
令z=,得n1=(3,2,).
∵DE⊥平面PAB,
∴平面PAB的法向量为n2=(0,1,0).
设二面角A?PB?E的大小为θ,
由图知,cos θ=|cos〈n1,n2〉|==,θ=60°,
∴二面角A?PB?E的大小为60°.
20.解析:解法一:(1)证明:∵PB=PC,∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,∴PO⊥平面ABCD.
在梯形ABCD中,可得Rt△ABO≌Rt△BCD,
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,即AO⊥BD.
∵PA在平面ABCD内的射影为AO,∴PA⊥BD.
(2)∵DC⊥BC,且平面PBC⊥平面ABCD,
∴DC⊥平面PBC.
∵PC?平面PBC,∴DC⊥PC,
∴∠PCB为二面角P?DC?B的平面角.
∵△PBC是等边三角形,∴∠PCB=60°,即二面角P?DC?B的大小为60°.
(3)证明:取PB的中点N,连接CN.
∵PC=BC,∴CN⊥PB,①
∵AB⊥BC,且平面PBC⊥平面ABCD,
∴AB⊥平面PBC.
∵AB?平面PAB,
∴平面PBC⊥平面PAB.②
由①,②知CN⊥平面PAB.
取PA的中点M,连接DM,MN,则由MN∥AB∥CD,
MN=AB=CD,得四边形MNCD为平行四边形,
∴CN∥DM,∴DM⊥平面PAB.
∵DM?平面PAD,∴平面PAD⊥平面PAB.
解法二:取BC的中点O,因为△PBC是等边三角形,由侧面PBC⊥底面ABCD,得PO⊥底面ABCD.
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O?xyz.
(1)证明:∵CD=1,∴在直角梯形中,AB=BC=2,
在等边三角形PBC中,PO=,
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,),
∴=(-2,-1,0),=(1,-2,-),
∵·=(-2)×1+(-1)×(-2)+0×(-)=0,
∴⊥,即PA⊥BD.
(2)取PC中点N,则=.
∵=(0,2,0),=(1,0,),
∴·=×0+0×2+×0=0,
·=×1+0×0+×=0,
∴⊥平面PDC,显然=(0,0,),且⊥平面ABCD,
∴,的夹角等于所求二面角的平面角.
∵·=×0+0×0+×=,||=,||=,
∴cos〈,〉==,
∴二面角P?DC?B的大小为60°.
(3)证明:取PA的中点M,连接DM,
则M的坐标为.
又=,=(1,0,-),
∴·=×1+0×(-2)+×(-)=0,
·=×1+0×0+×(-)=0,
∴⊥,⊥,
即DM⊥PA,DM⊥PB.
又∵PA∩PB=P,
∴DM⊥平面PAB,
∴平面PAD⊥平面PAB.
21.解析:(1)由于PA⊥平面ABCD,CD?平面ABCD,则PA⊥CD,
由题意可知AD⊥CD,且PA∩AD=A,
由线面垂直的判定定理可得CD⊥平面PAD.
(2)以点A为坐标原点,平面ABCD内与AD垂直的直线为x轴,AD,AP方向为y轴,z轴建立如图所示的空间直角坐标系A?xyz,
易知:A(0,0,0),P(0,0,2),C(2,2,0),D(0,2,0),
由=可得点F的坐标为F,则=,
由=可得E(0,1,1),则=(0,1,1),
设平面AEF的法向量为:m=(x,y,z),则
据此可得平面AEF的一个法向量为:m=(1,1,-1),
很明显平面AEP的一个法向量为n=(1,0,0),
cos〈m,n〉===,
二面角F?AE?P的平面角为锐角,故二面角F?AE?P的余弦值为.
(3)易知P(0,0,2),B(2,-1,0),由=可得G,
则=,
由(2)知平面AEF的一个法向量为:m=(1,1,-1),
又m·=0且点A在平面AEF内,故直线AG在平面AEF内.
22.解析:(1)在三棱柱ABC?A1B1C1中,
∵CC1⊥平面ABC,
∴四边形A1ACC1为矩形.
又E,F分别为AC,A1C1的中点,
∴AC⊥EF.
∵AB=BC.
∴AC⊥BE,又EF∩BE=E,EF?平面BEF,BE?平面BEF,
∴AC⊥平面BEF.
(2)由(1)知AC⊥EF,AC⊥BE,EF∥CC1.
又CC1⊥平面ABC,∴EF⊥平面ABC.
∵BE?平面ABC,∴EF⊥BE.
如图建立空间直角坐标系E?xyz.
由题意得B(0,2,0),C(-1,0,0),D(1,0,1),F(0,0,2),G(0,2,1).
∴=(2,0,1),=(1,2,0),
设平面BCD的法向量为n=(a,b,c),
∴,∴,
令a=2,则b=-1,c=-4,
∴平面BCD的法向量n=(2,-1,-4),
又∵平面CDC1的法向量为=(0,2,0),
∴cos〈n·〉==-.
由图可得二面角B?CD?C1为钝角,所以二面角B?CD?C1的余弦值为-.
(3)由(2)知平面BCD的法向量为n=(2,-1,-4),∵G(0,2,1),F(0,0,2),
∴=(0,-2,1),∴n·=-2,∴n与不垂直,
∴GF与平面BCD不平行且不在平面BCD内,∴GF与平面BCD相交.
