22.3实践与探索(面积问题)-华东师大版九年级数学上册课件(共16张PPT)
文档属性
| 名称 | 22.3实践与探索(面积问题)-华东师大版九年级数学上册课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 15:23:44 | ||
图片预览

文档简介
(共16张PPT)
§22.3实践与探索(1)
——面积问题
知识回顾
1、列一元一次方程解应用题的步骤:
审
设
列
解
验
答
2、列方程解应用题必须掌握一些基本量间的关系:
路程=____________;
速度×时间
工作量=__________________;
工作效率×工作时间
利润=____________;
售价—
进价
利息=__________________。
本金×利率×期数
3、列方程解应用题还必须弄清一些关键词语的含义:
“和”、
“差”、
“倍”、
“分”、
“多”、
“少”、
“提前”、
“同时”、
“早到”、
“增加”、
“减少”。
步骤梳理
知识点1:列一元二次方程方程解应用题步骤
(1)审:即审题。弄清已知量、未知量以及它们之间的关系。
(2)设:即设未知数。分为直接和间接设未知数两种。设未知数时注意语句完整,带好单位。
(3)列:即列方程。正确找出题中的等量关系列出方程。特别注意方程两边的单位统一。
(4)解:即求出所列方程的解。省略解方程的过程。
(5)验:即检验。检验方程的解是否符合实际问题的要求。
(6)答:即写出答案。语句完整,带好单位。
应用题类型梳理
知识点2:列一元二次方程方程解应用题常见类型
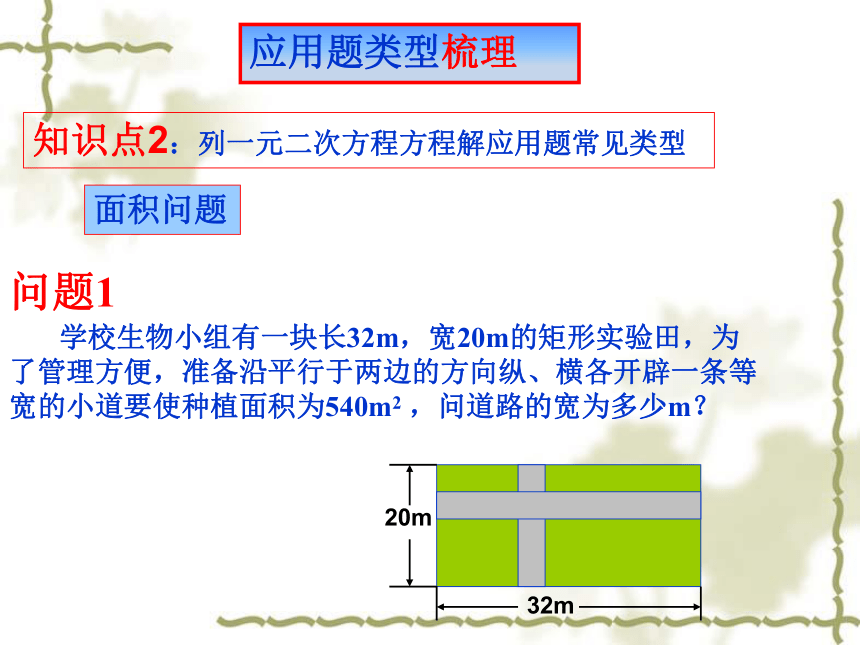
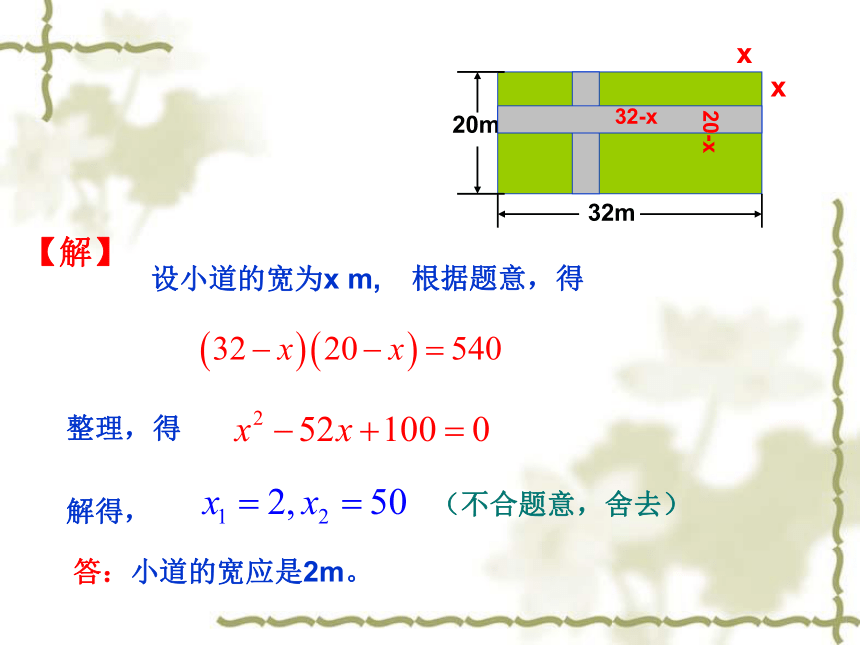
学校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道要使种植面积为540m2
,问道路的宽为多少m?
面积问题
问题1
32m
20m
32m
20m
x
x
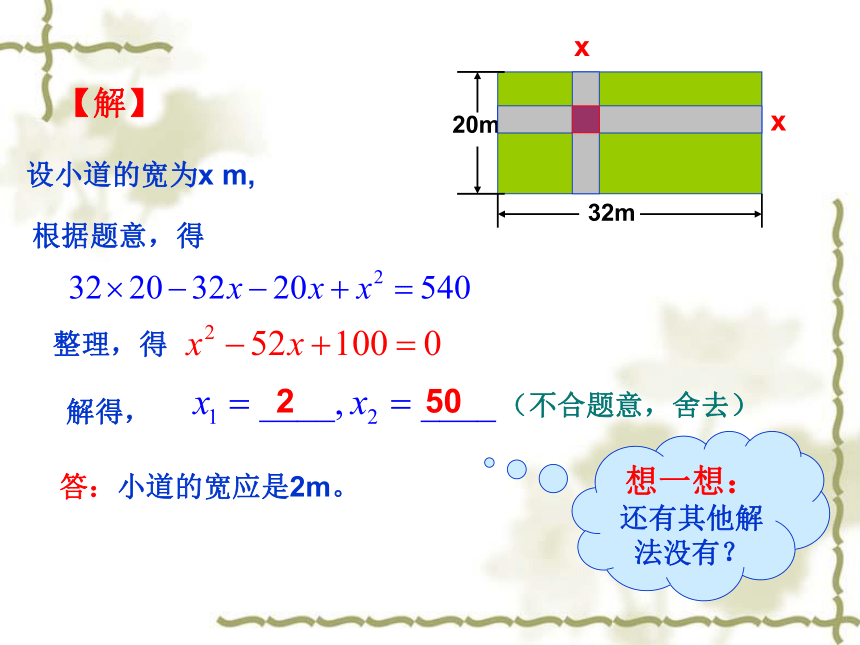
【解】
设小道的宽为x
m,
根据题意,得
整理,得
解得,
2
50
(不合题意,舍去)
答:小道的宽应是2m。
想一想:
还有其他解法没有?
32m
20m
x
x
【解】
设小道的宽为x
m,
根据题意,得
整理,得
解得,
(不合题意,舍去)
答:小道的宽应是2m。
32-x
20-x
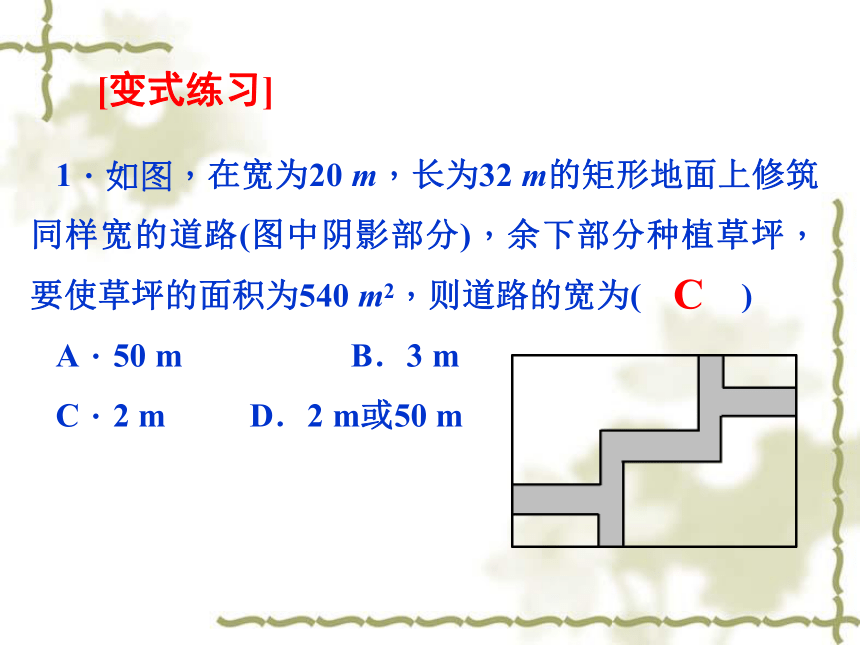
1.如图,在宽为20
m,长为32
m的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540
m2,则道路的宽为(
)
A.50
m B.3
m
C.2
m
D.2
m或50
m
C
[变式练习]
2.如图,在一块长35
m、宽26
m的矩形绿地上有宽度相同的两条小路,其中绿地面积为850
m2,求小路的宽.设小路宽为x
m,则可列方程___________________.
(35-x)(26-x)=850
[变式练习]
3.如图,是某小区在一块长为40
m,宽为26
m的矩形场地ABCD上修建的三条同样宽的甬道,其中两条与AB平行,另一条与AD平行,其余部分种上草,若使草坪的面积为864
m2,求甬道的宽度.
[变式练习]
设甬道的宽度为x
m,则可列方程___________________.
(40-2x)(26-x)=864
对应练习
(课本P40练习)
学生会准备举办一次摄影展览,在每张长和宽分别为18厘
米和12厘米的矩形相片周围镶上一圈等宽的彩纸。经试验,彩
纸面积为相片面积的
时较美观,求所镶彩纸的宽。(精确
到0.1厘米)
12
18
18
12
x
x
x
x
【解】
设彩纸宽为x厘米,
根据题意,得
整理,得
解得,
(不合题意,舍去)
答:所镶彩纸的宽约是2.1厘米。
1.某种洗衣机的包装箱外形是长方体,其高为1.2
m,体积为1.2
m3,底面是正方形,则该包装箱的表面积为__________m2.
6.8
课堂练习
课堂练习
2.如图,△ABC中,∠B=90°,点P从点A开始,沿AB边向B以1
cm/s的速度移动,点Q从点B开始沿BC边向点C以2
cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒钟,使△PBQ的面积等于8
cm2?
3.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12
m的住房墙,另外三边用25
m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1
m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2
?
课堂练习
课堂小结
1、弄清列一元二次方程解应用题的步骤。
2、列方程解应用题的关键:
①用含未知数的代数式正确表示有关的量;
②正确找出包含题目全部意义的一个等量关系。
3、形积问题注意:
识记各种几何图形的面积和几何体的体积公式。对于面积问题,一是要牢记常见几何图形的面积公式,二是注意利用化归思想进行转化,根据图形的特点,灵活处理不规则图形.
课堂作业:P.42
习题22.3
1、3、4
§22.3实践与探索(1)
——面积问题
知识回顾
1、列一元一次方程解应用题的步骤:
审
设
列
解
验
答
2、列方程解应用题必须掌握一些基本量间的关系:
路程=____________;
速度×时间
工作量=__________________;
工作效率×工作时间
利润=____________;
售价—
进价
利息=__________________。
本金×利率×期数
3、列方程解应用题还必须弄清一些关键词语的含义:
“和”、
“差”、
“倍”、
“分”、
“多”、
“少”、
“提前”、
“同时”、
“早到”、
“增加”、
“减少”。
步骤梳理
知识点1:列一元二次方程方程解应用题步骤
(1)审:即审题。弄清已知量、未知量以及它们之间的关系。
(2)设:即设未知数。分为直接和间接设未知数两种。设未知数时注意语句完整,带好单位。
(3)列:即列方程。正确找出题中的等量关系列出方程。特别注意方程两边的单位统一。
(4)解:即求出所列方程的解。省略解方程的过程。
(5)验:即检验。检验方程的解是否符合实际问题的要求。
(6)答:即写出答案。语句完整,带好单位。
应用题类型梳理
知识点2:列一元二次方程方程解应用题常见类型
学校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道要使种植面积为540m2
,问道路的宽为多少m?
面积问题
问题1
32m
20m
32m
20m
x
x
【解】
设小道的宽为x
m,
根据题意,得
整理,得
解得,
2
50
(不合题意,舍去)
答:小道的宽应是2m。
想一想:
还有其他解法没有?
32m
20m
x
x
【解】
设小道的宽为x
m,
根据题意,得
整理,得
解得,
(不合题意,舍去)
答:小道的宽应是2m。
32-x
20-x
1.如图,在宽为20
m,长为32
m的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540
m2,则道路的宽为(
)
A.50
m B.3
m
C.2
m
D.2
m或50
m
C
[变式练习]
2.如图,在一块长35
m、宽26
m的矩形绿地上有宽度相同的两条小路,其中绿地面积为850
m2,求小路的宽.设小路宽为x
m,则可列方程___________________.
(35-x)(26-x)=850
[变式练习]
3.如图,是某小区在一块长为40
m,宽为26
m的矩形场地ABCD上修建的三条同样宽的甬道,其中两条与AB平行,另一条与AD平行,其余部分种上草,若使草坪的面积为864
m2,求甬道的宽度.
[变式练习]
设甬道的宽度为x
m,则可列方程___________________.
(40-2x)(26-x)=864
对应练习
(课本P40练习)
学生会准备举办一次摄影展览,在每张长和宽分别为18厘
米和12厘米的矩形相片周围镶上一圈等宽的彩纸。经试验,彩
纸面积为相片面积的
时较美观,求所镶彩纸的宽。(精确
到0.1厘米)
12
18
18
12
x
x
x
x
【解】
设彩纸宽为x厘米,
根据题意,得
整理,得
解得,
(不合题意,舍去)
答:所镶彩纸的宽约是2.1厘米。
1.某种洗衣机的包装箱外形是长方体,其高为1.2
m,体积为1.2
m3,底面是正方形,则该包装箱的表面积为__________m2.
6.8
课堂练习
课堂练习
2.如图,△ABC中,∠B=90°,点P从点A开始,沿AB边向B以1
cm/s的速度移动,点Q从点B开始沿BC边向点C以2
cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒钟,使△PBQ的面积等于8
cm2?
3.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12
m的住房墙,另外三边用25
m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1
m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2
?
课堂练习
课堂小结
1、弄清列一元二次方程解应用题的步骤。
2、列方程解应用题的关键:
①用含未知数的代数式正确表示有关的量;
②正确找出包含题目全部意义的一个等量关系。
3、形积问题注意:
识记各种几何图形的面积和几何体的体积公式。对于面积问题,一是要牢记常见几何图形的面积公式,二是注意利用化归思想进行转化,根据图形的特点,灵活处理不规则图形.
课堂作业:P.42
习题22.3
1、3、4
