人教版八年级上册 数学 课件: 13.4 课题学习 最短路径问题(共21张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 课件: 13.4 课题学习 最短路径问题(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 204.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 15:31:53 | ||
图片预览





文档简介
(共21张PPT)
13.4
课题学习 最短路径问题
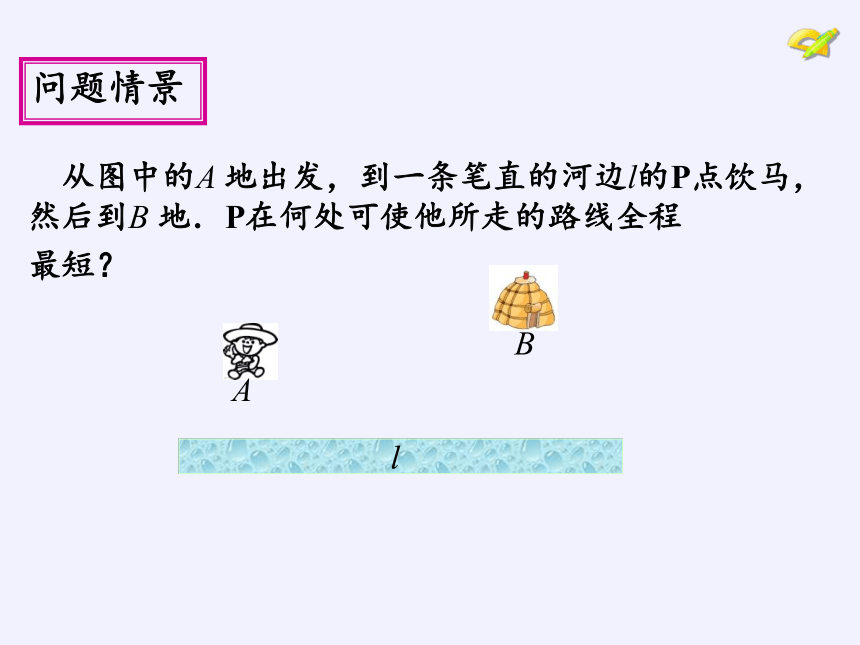
从图中的A
地出发,到一条笔直的河边l的P点饮马,然后到B
地.P在何处可使他所走的路线全程
最短?
问题情景
B
A
l
追问1 这是一个实际问题,你打算首先做什么?
将A,B
两地抽象为两个点,将河l
抽象为一条直
线.
B
·
·
A
l
这样做的理由是什么?
知识回顾
探求平面内最短路径的主要原理有以下两种:一是“垂线段最短”,二是“两点之间,线段最短”,求平面内折线的最短路径的最短路径通常用轴对称变换、平移变换、旋转变换转化为“两点之间的线段”。立体图形上的最短路径问题常需借助平面展开图转化为平面问题。
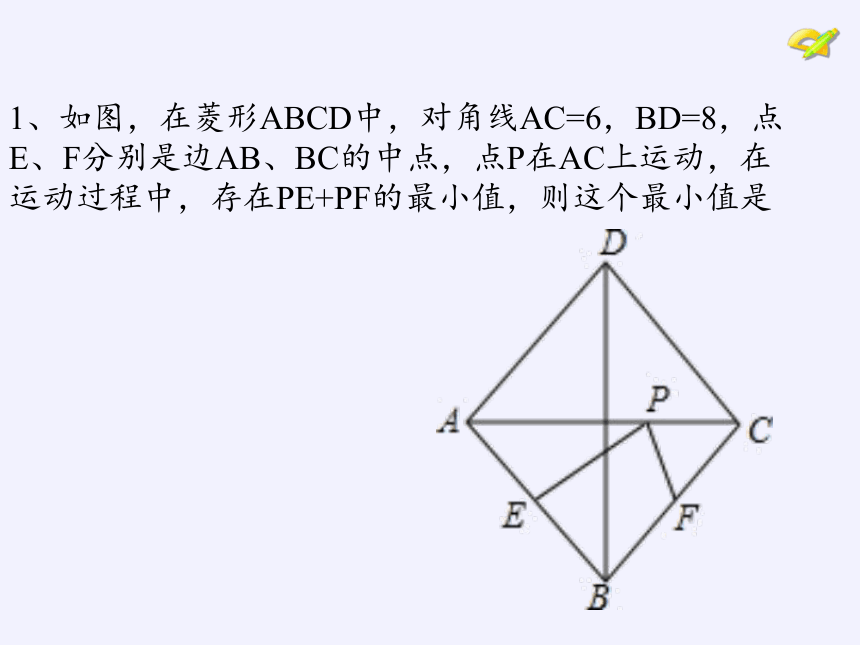
1、如图,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是
2、如图,正方形ABCD的边长是2,以正方形ABCD的边AB为边,在正方形内作等边三角形ABE,P为对角线AC上的一点,则PD+PE的最小值为______.
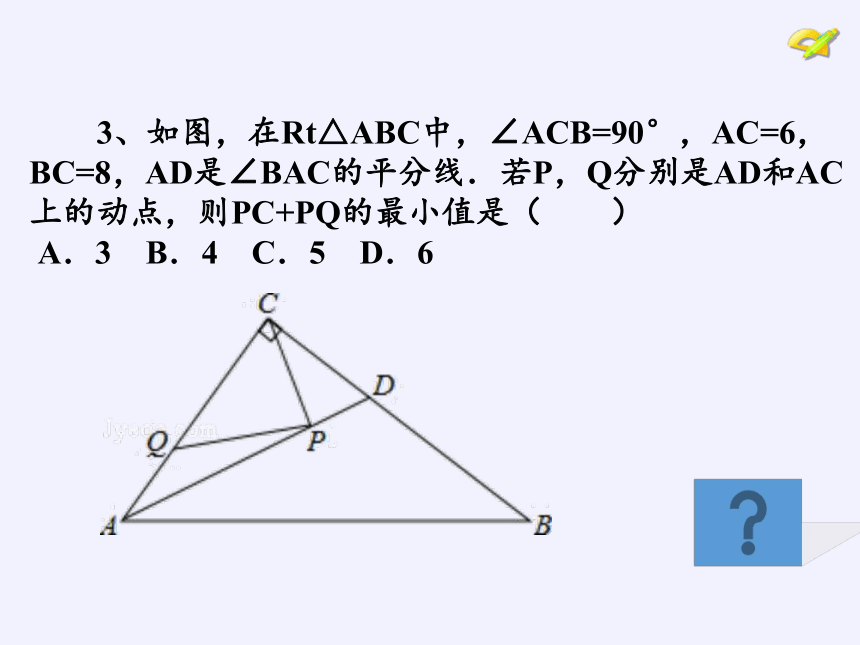
3、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A.3
B.4
C.5
D.6
4、如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
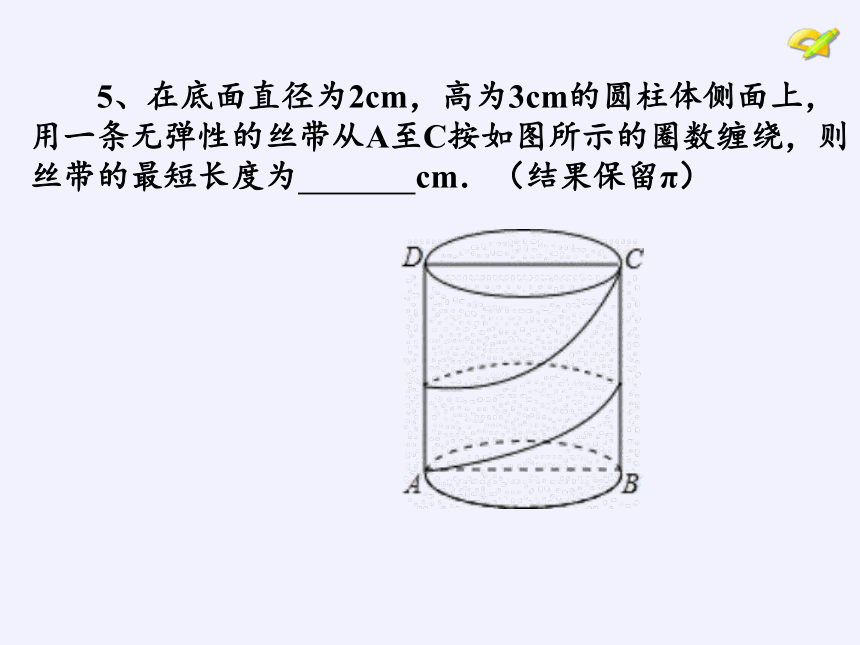
5、在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为
cm.(结果保留π)
6、如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
课堂回顾:本节课你复习了什么内容?通过本节课复习,你有何收获?
探求平面内最短路径的主要原理有以下两种:一是“垂线段最短”,二是“两点之间,线段最短”,求平面内折线的最短路径的最短路径通常用轴对称变换、平移变换、旋转变换转化为“两点之间的线段”。立体图形上的最短路径问题常需借助平面展开图转化为平面问题。
谢谢指教!
问题3 你能用所学的知识证明AC
+BC最短吗?
B
·
l
A
·
B′
C
C′
证明:在△AB′C′中,
AB′<AC′+B′C′,
∴ AC
+BC<AC′+BC′.
即 AC
+BC
最短.
若直线l
上任意一点(与点
C
不重合)与A,B
两点的距离
和都大于AC
+BC,就说明AC
+
BC
最小.
B
·
l
A
·
B′
C
C′
追问1 证明AC
+BC
最短时,为什么要在直线l
上
任取一点C′(与点C
不重合),证明AC
+BC
<AC′
+BC′?这里的“C′”的作用是什么?
追问2 回顾前面的探究过程,我们是通过怎样的
过程、借助什么解决问题的?
B
·
l
A
·
B′
C
C′
如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
解:沿AC-CD-DB路线走是最短的路线如图(1)所示:
证明:在ON上任意取一点T,在OM上任意取一点R,连接FR、BR、RT、ET、AT,
∵A、E关于ON对称,
∴AC=EC,
某班举行文艺晚会,桌子摆成两直条(如图1中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短?
运用新知
练习 如图,一个旅游船从大桥AB
的P
处前往山
脚下的Q
处接游客,然后将游客送往河岸BC
上,再返
回P
处,请画出旅游船的最短路径.
A
B
C
P
Q
山
河岸
大桥
基本思路:
由于两点之间线段最短,所以首先可连接PQ,线
段PQ
为旅游船最短路径中的必经线路.将河岸抽象为
一条直线BC,这样问题就转化为“点P,Q
在直线BC
的同侧,如何在BC上找到
一点R,使PR与QR
的和最
小”.
A
B
C
P
Q
山
河岸
大桥
谢
谢
13.4
课题学习 最短路径问题
从图中的A
地出发,到一条笔直的河边l的P点饮马,然后到B
地.P在何处可使他所走的路线全程
最短?
问题情景
B
A
l
追问1 这是一个实际问题,你打算首先做什么?
将A,B
两地抽象为两个点,将河l
抽象为一条直
线.
B
·
·
A
l
这样做的理由是什么?
知识回顾
探求平面内最短路径的主要原理有以下两种:一是“垂线段最短”,二是“两点之间,线段最短”,求平面内折线的最短路径的最短路径通常用轴对称变换、平移变换、旋转变换转化为“两点之间的线段”。立体图形上的最短路径问题常需借助平面展开图转化为平面问题。
1、如图,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是
2、如图,正方形ABCD的边长是2,以正方形ABCD的边AB为边,在正方形内作等边三角形ABE,P为对角线AC上的一点,则PD+PE的最小值为______.
3、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A.3
B.4
C.5
D.6
4、如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
5、在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为
cm.(结果保留π)
6、如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
课堂回顾:本节课你复习了什么内容?通过本节课复习,你有何收获?
探求平面内最短路径的主要原理有以下两种:一是“垂线段最短”,二是“两点之间,线段最短”,求平面内折线的最短路径的最短路径通常用轴对称变换、平移变换、旋转变换转化为“两点之间的线段”。立体图形上的最短路径问题常需借助平面展开图转化为平面问题。
谢谢指教!
问题3 你能用所学的知识证明AC
+BC最短吗?
B
·
l
A
·
B′
C
C′
证明:在△AB′C′中,
AB′<AC′+B′C′,
∴ AC
+BC<AC′+BC′.
即 AC
+BC
最短.
若直线l
上任意一点(与点
C
不重合)与A,B
两点的距离
和都大于AC
+BC,就说明AC
+
BC
最小.
B
·
l
A
·
B′
C
C′
追问1 证明AC
+BC
最短时,为什么要在直线l
上
任取一点C′(与点C
不重合),证明AC
+BC
<AC′
+BC′?这里的“C′”的作用是什么?
追问2 回顾前面的探究过程,我们是通过怎样的
过程、借助什么解决问题的?
B
·
l
A
·
B′
C
C′
如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
解:沿AC-CD-DB路线走是最短的路线如图(1)所示:
证明:在ON上任意取一点T,在OM上任意取一点R,连接FR、BR、RT、ET、AT,
∵A、E关于ON对称,
∴AC=EC,
某班举行文艺晚会,桌子摆成两直条(如图1中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短?
运用新知
练习 如图,一个旅游船从大桥AB
的P
处前往山
脚下的Q
处接游客,然后将游客送往河岸BC
上,再返
回P
处,请画出旅游船的最短路径.
A
B
C
P
Q
山
河岸
大桥
基本思路:
由于两点之间线段最短,所以首先可连接PQ,线
段PQ
为旅游船最短路径中的必经线路.将河岸抽象为
一条直线BC,这样问题就转化为“点P,Q
在直线BC
的同侧,如何在BC上找到
一点R,使PR与QR
的和最
小”.
A
B
C
P
Q
山
河岸
大桥
谢
谢
