人教版八年级上册 12.2 三角形全等的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册 12.2 三角形全等的判定 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 11:04:08 | ||
图片预览




文档简介
三角形全等的判定
同步练习
一.选择题
1.根据下列条件,能画出唯一的三角形ABC的是( )
A.AB=3,BC=4,AC=8
B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=50°
D.∠A=30°,∠B=70°,∠C=80°
2.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.PQ
B.MO
C.PA
D.MQ
3.如图,已知∠1=∠2,添加下列某条件,未必能判定△ABC≌△BAD的是( )
A.∠DAB=∠CBA
B.∠C=∠D
C.BD=AC
D.AD=BC
4.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,则这样的点P有( )
A.1个
B.2个
C.3个
D.4个
5.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是( )
A.①②
B.②③
C.③④
D.只有④
6.如图,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他的依据是( )
A.ASA
B.SAS
C.SSS
D.AAS
7.如图,AD,BC相交于点O,且AO=DO,BO=CO,则△ABO≌△DCO,理由是( )
A.SSS
B.SAS
C.ASA
D.AAS
8.下列给出的四组已知条件:①AB=10cm,BC=6cm,AC=13cm;②AB=10cm,∠A=35°,∠B=70°;③AB=10cm,∠C=90°,BC=6cm;④AB=10cm,∠A=60°,BC=10cm.其中可以画出唯一确定△ABC的有( )
A.1组
B.2组
C.3组
D.4组
9.在△ABC与△DEF中,下列六个条件中:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F,不能判断△ABC与△DEF全等的是( )
A.①②④
B.①②③
C.④⑥①
D.②③⑥
10.如图,AB⊥CD,CE⊥AF,BF⊥ED.若AB=CD,CE=8,BF=6,AD=10,则EF的长为( )
A.4
B.3.5
C.3
D.2.5
11.已知CD⊥AB于点D,现有四个条件,那么不能得出△ADC≌△EDB的条件是( )
①AD=ED:②∠A=∠BED;③∠C=∠B;④CD=BD.
A.①③
B.②④
C.①④
D.②③
12.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的是( )
A.①②③
B.①③④
C.②③④
D.①②
二.填空题
13.如图,AB∥CD,AD∥BC,EF过AC与BD的交点O.图中全等三角形有
对.
14.在△ABC和△DEF中,给出下列四组条件:
①∠B=∠E,BC=EF,∠C=∠F;
②AB=DE,∠B=∠E,BC=EF;
③AB=DE,BC=EF,AC=DF;
④AB=DE,AC=DF,∠B=∠E;
其中,不能使△ABC≌△DEF的条件是
.(填写序号)
15.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,∠BAD=22°,∠ACE=30°,则∠ADE=
.
16.如图,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=3BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ACF与△BDE的面积之和为
.
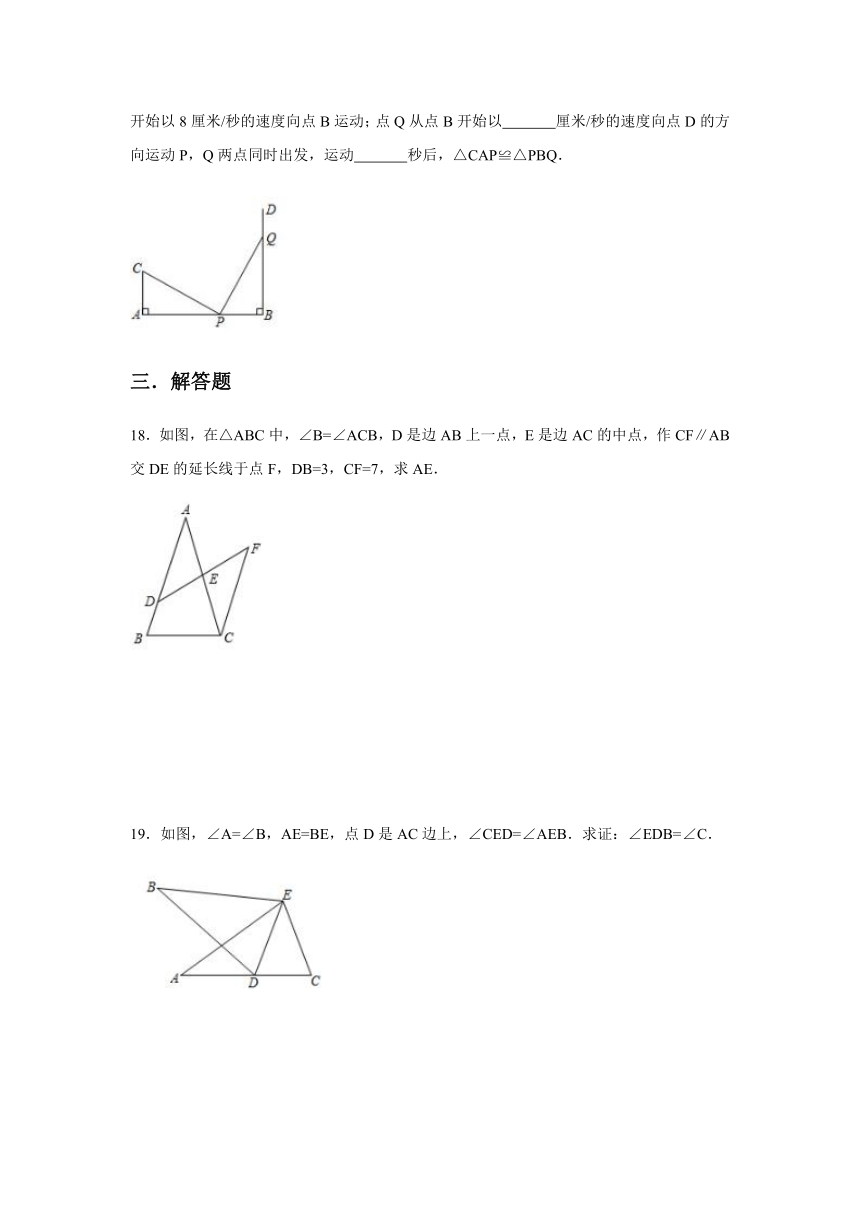
17.如图,AB=150厘米,CA⊥AB于点A,DB⊥AB于点B,且AC=30厘米.点P从点A开始以8厘米/秒的速度向点B运动;点Q从点B开始以
厘米/秒的速度向点D的方向运动P,Q两点同时出发,运动
秒后,△CAP≌△PBQ.
三.解答题
18.如图,在△ABC中,∠B=∠ACB,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F,DB=3,CF=7,求AE.
19.如图,∠A=∠B,AE=BE,点D是AC边上,∠CED=∠AEB.求证:∠EDB=∠C.
20.已知:如图,AC、BD相交于点E,AB=DC,∠B=∠C.
求证:(1)△ABE≌△DCE;(2)∠BDA=∠CAD.
21.如图,要测量河流AB的长,因为无法测河流附近的点A,可以在AB线外任取一点D,在AB的延长线上任取一点E,连结ED和BD,并且延长BD到点G,使DG=BD;延长ED到点F,使DF=ED;连结FG,并延长FG到点H,使点H,D,A在同一直线上.证明:测量出线段HG的长就是河流AB的长.
22.如图,已知,AC为△ABD的高,DF交AC于E,交AB于F,连接BE,且有BE=AD,CE=CD.求证:
(1)△BCE≌△ACD;
(2)BE⊥AD.
参考答案
1-5:CADCD
6-10:ABDAA
11-12:DB
13、6
④
52°
3
8;15
18、:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
∴CF=AD=7,
∴AB=AD+BD=10,
又∵∠B=∠ACB,
∴AB=AC=10,
∵E是边AC的中点,
∴AE==5.
19、:∵∠BEA=∠CED
∴∠BEA+∠AED=∠CED+∠AED
既∠BED=∠CEA
∵∠A=∠B,AE=BE
∴△BED≌△AEC(ASA)
∴∠EDB=∠C.
20、(1)证明:在△ABE和△DCE中,
∴△ABE≌△DCE(AAS),
(2)由(1)得:△ABE≌△DCE
∴AE=DE,
∴∠CAD=∠BDA.
21、:∵DB=DG,∠BDE=∠GDF,DE=DF,
∴△BED≌△GFD(SAS),
∴∠EBD=∠FGD,
∴∠ABD=∠HGD
又∵BD=GD,∠ADB=∠HDG,
∴△ABD≌△DGH(ASA),
∴AB=GH,
∴测量出线段HG的长就是河流AB的长.
22、(1)证明:∵AC为△ABD的高,
∴AC⊥BD,
∴∠BCE=∠ACD=90°,
在Rt△BCE与Rt△ACD中,
∴Rt△BCE≌Rt△ACD(HL).
(2)延长BE交AD于点M,
∵△BCE≌△ACD(已证),
∴∠BEC=∠ADC=∠MDB,又∵AC⊥BC,
∴∠MBD+∠MDB=∠EBC+∠BEC=90°,
∴∠BMD=180°-(∠MBC+∠MDB)=180°-90°=90°,
∴BM⊥AD,
又∵B,E,M三点共线,
∴BE⊥AD.
同步练习
一.选择题
1.根据下列条件,能画出唯一的三角形ABC的是( )
A.AB=3,BC=4,AC=8
B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=50°
D.∠A=30°,∠B=70°,∠C=80°
2.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.PQ
B.MO
C.PA
D.MQ
3.如图,已知∠1=∠2,添加下列某条件,未必能判定△ABC≌△BAD的是( )
A.∠DAB=∠CBA
B.∠C=∠D
C.BD=AC
D.AD=BC
4.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,则这样的点P有( )
A.1个
B.2个
C.3个
D.4个
5.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是( )
A.①②
B.②③
C.③④
D.只有④
6.如图,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他的依据是( )
A.ASA
B.SAS
C.SSS
D.AAS
7.如图,AD,BC相交于点O,且AO=DO,BO=CO,则△ABO≌△DCO,理由是( )
A.SSS
B.SAS
C.ASA
D.AAS
8.下列给出的四组已知条件:①AB=10cm,BC=6cm,AC=13cm;②AB=10cm,∠A=35°,∠B=70°;③AB=10cm,∠C=90°,BC=6cm;④AB=10cm,∠A=60°,BC=10cm.其中可以画出唯一确定△ABC的有( )
A.1组
B.2组
C.3组
D.4组
9.在△ABC与△DEF中,下列六个条件中:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F,不能判断△ABC与△DEF全等的是( )
A.①②④
B.①②③
C.④⑥①
D.②③⑥
10.如图,AB⊥CD,CE⊥AF,BF⊥ED.若AB=CD,CE=8,BF=6,AD=10,则EF的长为( )
A.4
B.3.5
C.3
D.2.5
11.已知CD⊥AB于点D,现有四个条件,那么不能得出△ADC≌△EDB的条件是( )
①AD=ED:②∠A=∠BED;③∠C=∠B;④CD=BD.
A.①③
B.②④
C.①④
D.②③
12.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的是( )
A.①②③
B.①③④
C.②③④
D.①②
二.填空题
13.如图,AB∥CD,AD∥BC,EF过AC与BD的交点O.图中全等三角形有
对.
14.在△ABC和△DEF中,给出下列四组条件:
①∠B=∠E,BC=EF,∠C=∠F;
②AB=DE,∠B=∠E,BC=EF;
③AB=DE,BC=EF,AC=DF;
④AB=DE,AC=DF,∠B=∠E;
其中,不能使△ABC≌△DEF的条件是
.(填写序号)
15.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,∠BAD=22°,∠ACE=30°,则∠ADE=
.
16.如图,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=3BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ACF与△BDE的面积之和为
.
17.如图,AB=150厘米,CA⊥AB于点A,DB⊥AB于点B,且AC=30厘米.点P从点A开始以8厘米/秒的速度向点B运动;点Q从点B开始以
厘米/秒的速度向点D的方向运动P,Q两点同时出发,运动
秒后,△CAP≌△PBQ.
三.解答题
18.如图,在△ABC中,∠B=∠ACB,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F,DB=3,CF=7,求AE.
19.如图,∠A=∠B,AE=BE,点D是AC边上,∠CED=∠AEB.求证:∠EDB=∠C.
20.已知:如图,AC、BD相交于点E,AB=DC,∠B=∠C.
求证:(1)△ABE≌△DCE;(2)∠BDA=∠CAD.
21.如图,要测量河流AB的长,因为无法测河流附近的点A,可以在AB线外任取一点D,在AB的延长线上任取一点E,连结ED和BD,并且延长BD到点G,使DG=BD;延长ED到点F,使DF=ED;连结FG,并延长FG到点H,使点H,D,A在同一直线上.证明:测量出线段HG的长就是河流AB的长.
22.如图,已知,AC为△ABD的高,DF交AC于E,交AB于F,连接BE,且有BE=AD,CE=CD.求证:
(1)△BCE≌△ACD;
(2)BE⊥AD.
参考答案
1-5:CADCD
6-10:ABDAA
11-12:DB
13、6
④
52°
3
8;15
18、:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
∴CF=AD=7,
∴AB=AD+BD=10,
又∵∠B=∠ACB,
∴AB=AC=10,
∵E是边AC的中点,
∴AE==5.
19、:∵∠BEA=∠CED
∴∠BEA+∠AED=∠CED+∠AED
既∠BED=∠CEA
∵∠A=∠B,AE=BE
∴△BED≌△AEC(ASA)
∴∠EDB=∠C.
20、(1)证明:在△ABE和△DCE中,
∴△ABE≌△DCE(AAS),
(2)由(1)得:△ABE≌△DCE
∴AE=DE,
∴∠CAD=∠BDA.
21、:∵DB=DG,∠BDE=∠GDF,DE=DF,
∴△BED≌△GFD(SAS),
∴∠EBD=∠FGD,
∴∠ABD=∠HGD
又∵BD=GD,∠ADB=∠HDG,
∴△ABD≌△DGH(ASA),
∴AB=GH,
∴测量出线段HG的长就是河流AB的长.
22、(1)证明:∵AC为△ABD的高,
∴AC⊥BD,
∴∠BCE=∠ACD=90°,
在Rt△BCE与Rt△ACD中,
∴Rt△BCE≌Rt△ACD(HL).
(2)延长BE交AD于点M,
∵△BCE≌△ACD(已证),
∴∠BEC=∠ADC=∠MDB,又∵AC⊥BC,
∴∠MBD+∠MDB=∠EBC+∠BEC=90°,
∴∠BMD=180°-(∠MBC+∠MDB)=180°-90°=90°,
∴BM⊥AD,
又∵B,E,M三点共线,
∴BE⊥AD.
