行列式性质

(共26张PPT)
行列式性质
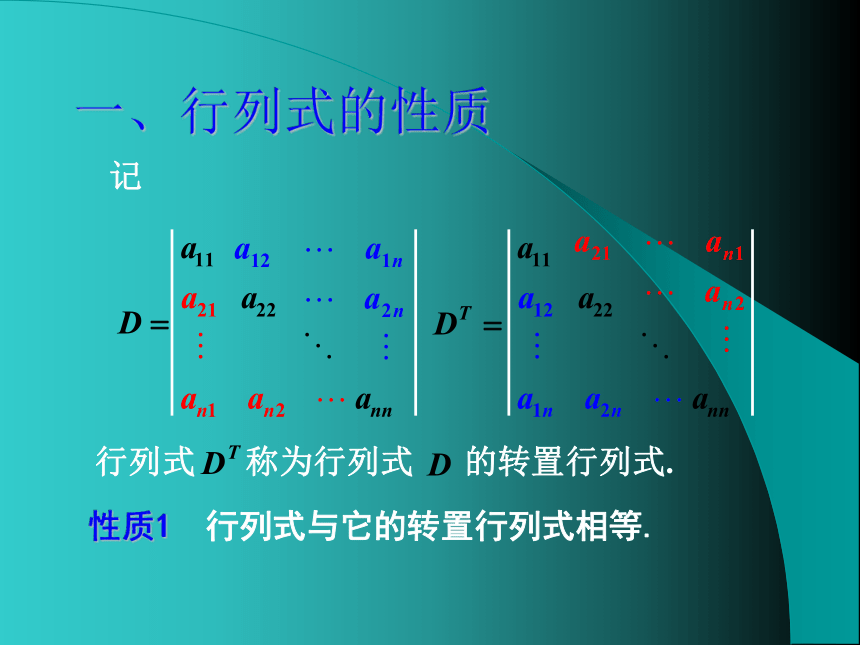
一、行列式的性质
性质1 行列式与它的转置行列式相等.
行列式 称为行列式 的转置行列式.
记
证明
按定义
又因为行列式D可表示为
故
证毕
性质2 互换行列式的两行（列）,行列式变号.
证明
设行列式
说明 行列式中行与列具有同等的地位,因此行列
式的性质凡是对行成立的对列也同样成立.
是由行列式 变换 两行得到的,
于是
则有
即当 时,
当 时,
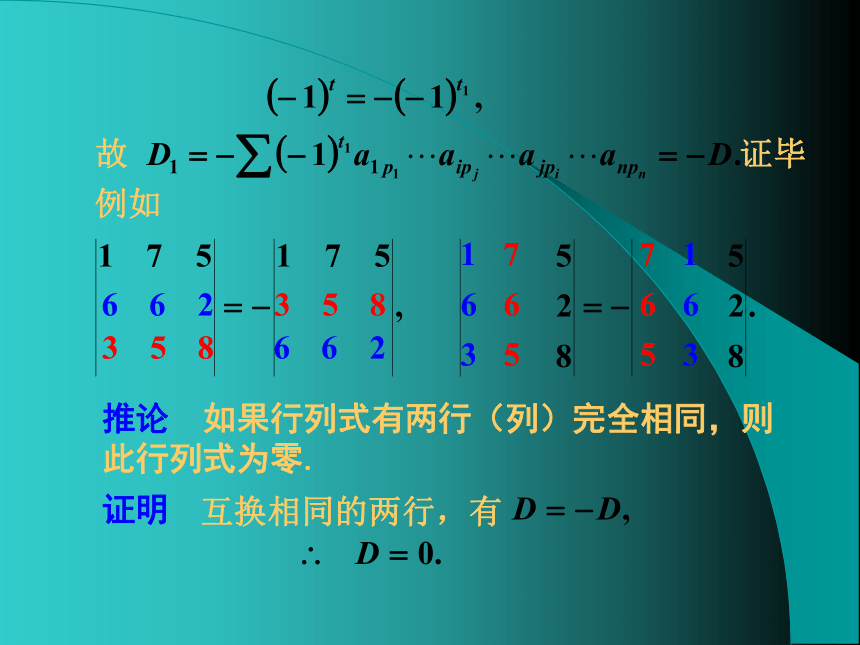
例如
推论 如果行列式有两行（列）完全相同，则此行列式为零.
证明
互换相同的两行，有
故
证毕
性质3 行列式的某一行（列）中所有的元素都乘以同一数 ，等于用数 乘此行列式.
推论　行列式的某一行（列）中所有元素的公因子可以提到行列式符号的外面．
性质４　行列式中如果有两行（列）元素成比例，则此行列式为零．
证明
性质5　若行列式的某一列（行）的元素都是两数之和.
则D等于下列两个行列式之和：
例如
性质６　把行列式的某一列（行）的各元素乘以同一数然后加到另一列(行)对应的元素上去，行列式不变．
例如
例１
二、应用举例
计算行列式常用方法：利用运算　　　把行列式化为上三角形行列式，从而算得行列式的值．
解
例2 计算 阶行列式
解
将第 都加到第一列得
例3
证明
证明
(行列式中行与列具有同等的地位,行列式的性质凡是对行成立的对列也同样成立).
计算行列式常用方法：(1)利用定义;(2)利用性质把行列式化为上三角形行列式，从而算得行列式的值．
三、小结
行列式的6个性质
思考题
思考题解答
解