4.2 圆的轴对称性（二）

(共14张PPT)
5.2. 圆的对称性(二)
苏州市胥江实验中学校
初中数学九年级上册
（苏科版）
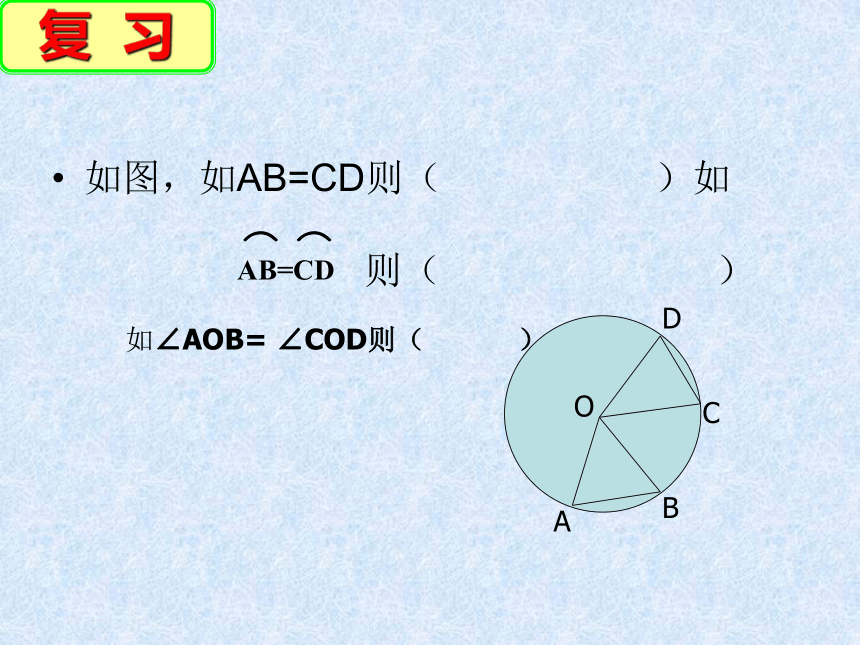
如图，如AB=CD则（ ）如
O
A
B
C
D
⌒
⌒
AB=CD
如∠AOB= ∠COD则（ ）
则（ ）
复 习
圆是轴对称图形吗？
它的对称轴是什么 你能找到多少条对称轴？
●O
你是用什么方法解决上述问题的
情景创设
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
交 流
③AM=BM,
AB是⊙O的一条弦.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
作直径CD,使CD⊥AB,垂足为M.
●O
下图是轴对称图形吗 如果是,其对称轴是什么
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
探 索
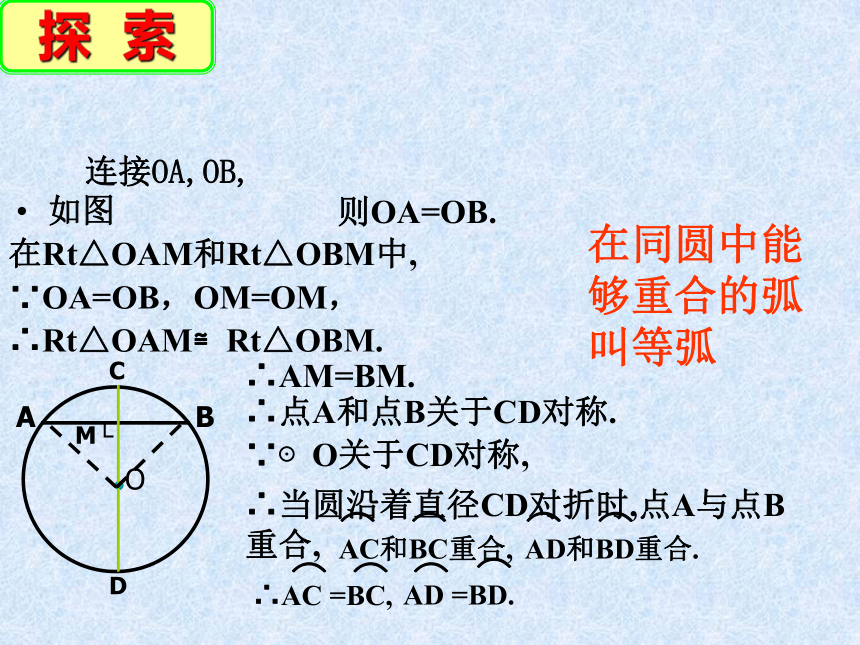
如图
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB，OM=OM，
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
　AD =BD.
在同圆中能够重合的弧叫等弧
探 索
定理 垂直于弦的直径平分弦,并且平分弦所对
的两 条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
条件
CD为直径
CD⊥AB
CD平分弧ADB
CD平分弦AB
CD平分弧A　B
结论
探 索
●O
A
B
C
D
M└
基本图形
例1. 已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点，AC与BD相等吗？为什么？
P
.
A
C
D
B
O
典型例题
例2：如图，已知在圆O中，弦AB的长为8㎝，
圆心O到AB的距离为3 ㎝，求圆O的半径。
变式1:在半径为5 ㎝的圆O中，有长8 ㎝的
　　弦AB，求点O与AB的距离。
　　
E
变式2：在半径为5 ㎝的圆O中，圆心O到弦AB的距离
为3 ㎝，求AB的长。
典型例题
2、在圆O中，直径CE⊥AB于
D，OD=4 ㎝，弦AC= ㎝ ，
求圆O的半径。
　　
1 、如图，
圆O的弦AB＝8 ㎝ ，
DC＝2㎝，直径CE⊥AB于D，
求半径OC的长。
练 习
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
A
B
拓 展
如图，CD为圆O的直径，弦
　　AB交CD于E， ∠ CEB=30°，
　　DE=9㎝，CE=3㎝，求弦AB的长。
思考题
通过本课的学习，你又有
什么收获？
回顾总结