2020_2021学年高中物理第十一章机械振动章末综合检测含解析新人教版选修3_4
文档属性
| 名称 | 2020_2021学年高中物理第十一章机械振动章末综合检测含解析新人教版选修3_4 |

|
|
| 格式 | zip | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览



文档简介
章末综合检测(第十一章)
时间:60分钟 满分:100分
一、选择题(本题共10个小题,1~6题为单项选择题,7~10题为多项选择题,每小题4分,共40分.)
1.关于简谐运动的回复力F=-kx的含义,下列说法正确的是( )
A.k是弹簧的劲度系数,x是弹簧的长度
B.k是回复力跟位移的比值,x是做简谐运动的物体离开平衡位置的位移
C.根据k=-,可以认为k与F成正比
D.表达式中的“-”号表示F始终阻碍物体的运动
2.
如图所示是某振子做简谐运动的图象,以下说法中正确的是( )
A.因为振动图象可由实验直接得到,所以图象就是振子实际运动的轨迹
B.振动图象反映的是振子位移随时间变化的规律,并不是振子运动的实际轨迹
C.振子在B位置的位移就是曲线BC的长度
D.振子运动到B点时的速度方向即为该点的切线方向
3.关于做简谐运动的单摆,下列说法正确的是( )
A.摆球经过平衡位置时所受合力为零
B.摆球所受合力的大小跟摆球相对平衡位置的位移大小成正比
C.只有在最高点时,回复力才等于重力和摆线拉力的合力
D.摆球在任意位置处,回复力都不等于重力和摆线拉力的合力
4.弹簧劲度系数为20
N/cm的水平弹簧振子,它的振动图象如图所示,下列说法正确的是( )
A.A点对应的时刻振子所受的弹力大小为0.5
N,方向指向x轴的负方向
B.A点对应的时刻振子的速度方向指向x轴的正方向
C.在0~4
s内振子做了1.75次全振动
D.在0~4
s内振子通过的路程为3.5
cm,位移为0
5.如图所示,图甲为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为该弹簧振子的振动图象,由图可知下列说法中正确的是( )
A.在t=0.2
s时,弹簧振子可能运动到B位置
B.在t=0.1
s与t=0.3
s两个时刻,弹簧振子的速度相同
C.从t=0到t=0.2
s的时间内,弹簧振子的动能持续地增加
D.在t=0.2
s与t=0.6
s两个时刻,弹簧振子的加速度相同
6.
一个做简谐运动的质点,先后以同样大小的速度通过相距10
cm的A、B两点,且由A到B的过程中速度方向不变,历时0.5
s(如图).过B点后再经过t=0.5
s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是( )
A.0.5
s B.1.0
s
C.2.0
s
D.4.0
s
7.一个弹簧振子的振幅是A,若在Δt的时间内物体运动的路程是s,则下列关系中可能正确的是(包括一定正确的)( )
A.Δt=2T,s=8A
B.Δt=,s=2A
C.Δt=,s=2A
D.Δt=,s>A
8.一弹簧振子在水平方向上做简谐运动,其位移x与时间t的关系曲线如图所示,在t=3.2
s时,振子的( )
A.速度正在增大,加速度沿正方向且正在减小
B.速度正在减小,回复力沿负方向且正在增大
C.动能正在转化为势能
D.势能正在转化为动能
9.如图甲所示,一弹簧振子在A、B间振动,取向右为正方向,振子经过O点时为计时时刻,其振动的x-t图象如图乙所示,则下列说法中正确的是( )
A.t2时刻振子在A点
B.t2时刻振子在B点
C.在t1~t2时间内,振子的位移在增大
D.在t3~t4时间内,振子的位移在减小
10.如图所示,下列说法正确的是( )
A.振动图象上的A,B两点的速度相同
B.在t=0.1
s和t=0.3
s时,质点的加速度大小相等,方向相反
C.振动图象上A,B两点的速度大小相等,方向相反
D.质点在t=0.2
s和t=0.3
s时的动能相等
二、非选择题(本题共6个小题,共60分)
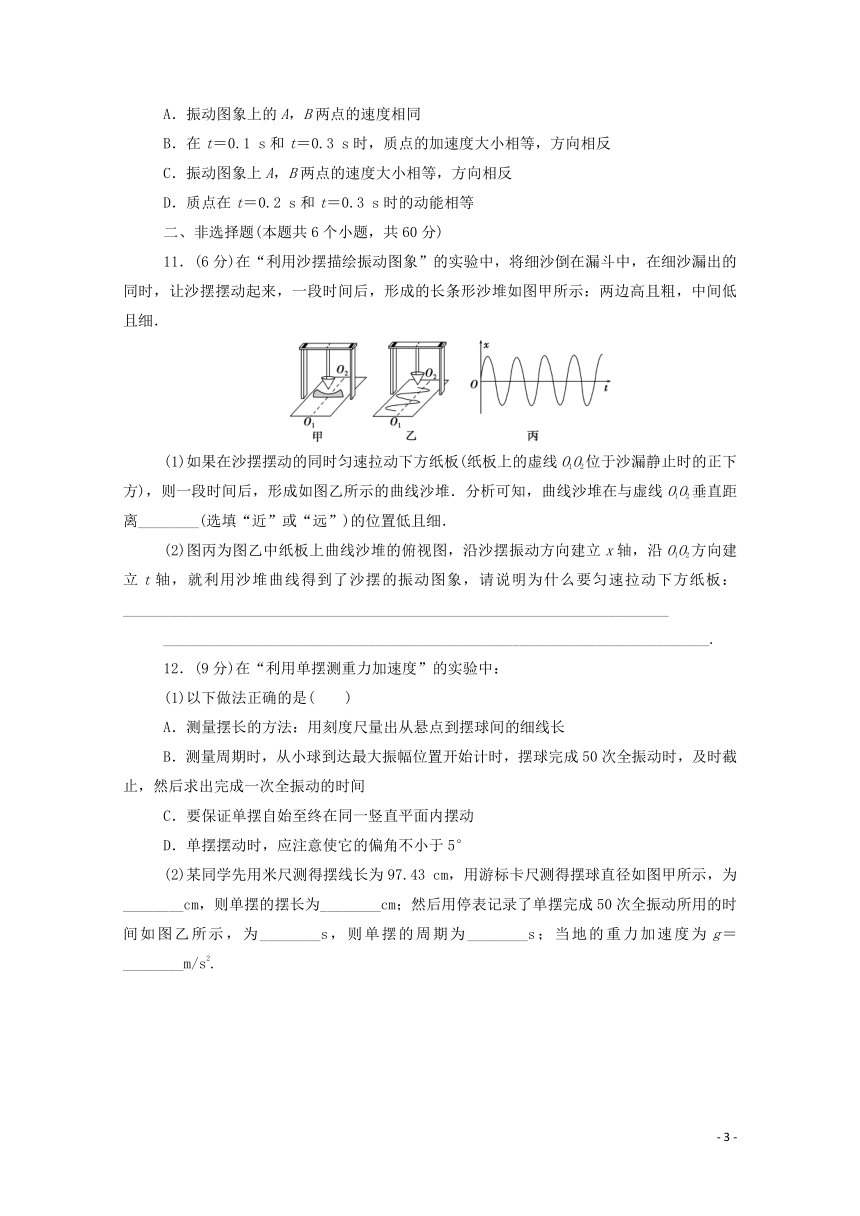
11.(6分)在“利用沙摆描绘振动图象”的实验中,将细沙倒在漏斗中,在细沙漏出的同时,让沙摆摆动起来,一段时间后,形成的长条形沙堆如图甲所示:两边高且粗,中间低且细.
(1)如果在沙摆摆动的同时匀速拉动下方纸板(纸板上的虚线O1O2位于沙漏静止时的正下方),则一段时间后,形成如图乙所示的曲线沙堆.分析可知,曲线沙堆在与虚线O1O2垂直距离________(选填“近”或“远”)的位置低且细.
(2)图丙为图乙中纸板上曲线沙堆的俯视图,沿沙摆振动方向建立x轴,沿O1O2方向建立t轴,就利用沙堆曲线得到了沙摆的振动图象,请说明为什么要匀速拉动下方纸板:________________________________________________________________________
________________________________________________________________________.
12.(9分)在“利用单摆测重力加速度”的实验中:
(1)以下做法正确的是( )
A.测量摆长的方法:用刻度尺量出从悬点到摆球间的细线长
B.测量周期时,从小球到达最大振幅位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间
C.要保证单摆自始至终在同一竖直平面内摆动
D.单摆摆动时,应注意使它的偏角不小于5°
(2)某同学先用米尺测得摆线长为97.43
cm,用游标卡尺测得摆球直径如图甲所示,为________cm,则单摆的摆长为________cm;然后用停表记录了单摆完成50次全振动所用的时间如图乙所示,为________s,则单摆的周期为________s;当地的重力加速度为g=________m/s2.
(3)实验中,如果摆球密度不均匀,就无法确定重心位置,一位同学设计了一个巧妙的方法不计摆球的半径.具体做法如下:第一次量得悬线长L1,测得振动周期为T1;第二次量得悬线长L2,测得振动周期为T2,由此可推得重力加速度为g=________.
13.(10分)甲、乙两个学习小组分别利用单摆测量重力加速度.
(1)甲组同学采用如图甲所示的实验装置.该组同学先测出悬点到小球球心的距离L,然后用秒表测出单摆完成n次全振动所用的时间t.请写出重力加速度的表达式g=________(用所测物理量表示).在测量摆长后,测量周期时,摆球振动过程中摆线略微变长,这将会导致所测重力加速度的数值________.(选填“偏大”“偏小”或“不变”)
(2)乙组同学在图甲所示装置的基础上再增加一个速度传感器,如图乙所示,将摆球拉开一小角度使其做简谐运动,速度传感器记录了摆球振动过程中速度随时间变化的关系,如图丙所示,由图丙可知,该单摆的周期T=________s.
(3)在多次改变摆线长度测量后,根据实验数据,利用计算机作出T2-L图线,并根据图线拟合得到方程T2=4.04L+0.0035.由此可以得出当地的重力加速度g=________m/s2.(取π2=9.86,结果保留三位有效数字)
14.(10分)如图所示为一弹簧振子的振动图象,求:
(1)从计时开始经多长时间第一次达到弹性势能最大?
(2)在2~3
s这段时间内弹簧振子的加速度、速度、动能和弹性势能各怎样变化?
(3)该振子在前100
s内的总位移是多少?路程是多少?
15.(10分)如图是一弹簧振子,O为平衡位置,B、C为两个极端位置,取向右为正方向,现把小球向右移动5
cm到B点,放手后发现小球经过1
s第一次到达C点,如果从B点放手时开始计时,求:
(1)小球做简谐运动的振幅、周期各是多少?
(2)写出小球运动的位移表达式.
(3)如果从小球经过平衡位置向左运动开始计时,则小球的位移表达式如何?
16.(15分)将一测力传感器连接到计算机上就可以测量快速变化的力.图(甲)表示小滑块(可视为质点)沿固定的光滑半球形容器内壁在竖直平面的A,A′之间来回滑动.A,A′点与O点连线与竖直方向之间夹角θ相等且很小,图(乙)表示滑块对器壁的压力F随时间t变化的曲线,图中t=0为滑块从A点开始运动的时刻.试根据力学规律和题中(包括图中)所给的信息,g取10
m/s2.求:
(1)容器的半径;
(2)小滑块的质量;
(3)滑块运动过程中的机械能.
章末综合检测(第十一章)
1.解析:对弹簧振子来说k为劲度系数,x为质点离开平衡位置位移大小,故A错误;对于其他简谐运动k不是劲度系数,而是一个比例系数,故B正确;该系数由系统本身结构决定,与力F和位移x无关,C错误;“-”只表示回复力与位移反向,回复力有时是动力,D错误.
答案:B
2.解析:振动图象表示位移随时间的变化规律,并不是运动轨迹,B对,A、C错.切线的方向只表示质点的速度方向与规定的正方向相同还是相反,不表示速度的方向.另外由于图象不是质点的运动轨迹,因此切线的方向并不表示速度的方向.
答案:B
3.解析:摆球经过平衡位置时,回复力为零,但由于摆球做圆周运动,经过平衡位置,合力不为零,合力提供向心力,方向指向悬点,A错误;摆球所受回复力由重力沿圆弧切线方向的分力提供,重力沿摆线方向的分力与摆线对摆球的拉力的合力提供向心力,所以摆球所受合力的大小跟摆球相对平衡位置的位移大小不成正比,B错误;根据牛顿第二定律可知,摆球在最大位移处时,速度为零,向心加速度为零,重力沿摆线方向的分力等于摆线对摆球的拉力,回复力才等于重力和摆线拉力的合力,在其他位置时,速度不为零,向心加速度不为零,重力沿摆线方向的分力小于摆线对摆球的拉力,回复力不等于重力和摆线拉力的合力,故C正确,D错误.
答案:C
4.解析:由图可知A点在t轴上方,位移x=0.25
cm,所以弹力F=-kx=-5
N,即弹力大小为5
N,方向指向x轴负方向,A项错误.由图可知A点对应的时刻振子的速度方向指向x轴的正方向,B项正确.由图可看出,t=0
s、t=2
s、t=4
s时刻振子的位移都是最大的,且都在t轴的上方,在0~4
s内完成两次全振动,C项错误.由于t=0时刻和t=4
s时刻振子都在最大位移处,所以在0~4
s内振子的位移为零,又由于振幅为0.5
cm,在0~4
s内振子完成了2次全振动,所以在这段时间内振子通过的路程为2×4×0.5
cm=4
cm,故D项错误.
答案:B
5.解析:t=0.2
s时,振子的位移为正的最大,但由于没有规定正方向,所以此时振子的位置可能在A点也可能在B点,A正确.t=0.1
s时速度为正,t=0.3
s时速度为负,两者方向相反,B错.从t=0到t=0.2
s的时间内,弹簧振子远离平衡位置,速度减小,动能减小,C错.t=0.2
s与t=0.6
s两个时刻,位移大小相等,方向相反,故加速度大小相等,方向相反,D错.
答案:A
6.解析:根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧.质点从平衡位置O向右运动到B的时间应为tOB=×0.5
s=0.25
s.质点从B向右到达右方极端位置(设为D)的时间tBD=×0.5
s=0.25
s.所以质点从O到D的时间tOD=T=0.25
s+0.25
s=0.5
s.所以T=2.0
s,C对.
答案:C
7.解析:因每个全振动所通过的路程为4A,每半个周期所通过的路程为2A,故A、B正确,C错误,又因振幅为振子的最大位移,而s为时的路程,故s有可能大于A,故D正确.
答案:ABD
8.解析:结合简谐运动的振动图象分析物理量的变化,由图可知,当=3.2
s时振子正在向最大位移处运动,位移为正向,速度正在减小,加速度和回复力沿负方向且正在增大,振子动能减小,弹簧弹性势能增大,动能正在转化为势能,B、C正确.A、D错误.
答案:BC
9.解析:振子在A点和B点时位移最大,由于取向右为正方向,所以振子运动到A点有正向最大位移,在B点有负向最大位移,则t2时刻,振子在A点,t4时刻,振子在B点,故选项A正确,B错误;振子的位移是以平衡位置为起点,所以在t1~t2和t3~t4时间内振子的位移都在增大,故选项C正确,D错误.
答案:AC
10.解析:A,B两点位移相同,但在A点时质点正远离平衡位置,在B点时质点正衡位置,所以图象上A,B两点速度大小相等,方向相反,选项A错误,C正确;t=0.1
s和t=0.3
s时,质点分别处在正、负最大位移处,加速度为最大值,但方向相反,选项B正确;t=0.2
s时,质点速度最大,动能最大,
t=0.3
s时,质点速度最小为零,动能为零,选项D错误.
答案:BC
11.解析:(1)单摆在摆动的过程中是变速运动,经过平衡位置的速度最大,最大位移处的速度为0;在相同的时间内漏下的沙子一样多,但在平衡位置附近速度大,相同时间内经过的距离长,故漏下的沙子低且细;
(2)只有拉动木板的速度恒定时,木板的位移与时间成正比,这样建立的位移轴才可以代表时间轴.
答案:(1)近 (2)只有拉动木板的速度恒定时,木板的位移与时间成正比,这样建立的位移轴才可以代表时间轴
12.解析:(1)单摆的摆长应为摆线长度加上摆球的半径,A选项错误;以摆球通过平衡位置(速度最大处)为计时起点可以减小计时误差,B选项错误;单摆摆动时应保持在同一竖直平面内,C选项正确;单摆振动过程中偏角应不超过5°,D选项错误.
(2)摆球直径为(21+5×0.05)
mm
=21.25
mm=2.125
cm.
摆长l=(97.43+)
cm=98.49
cm.
停表读数为(90+10.0)
s=100.0
s.
周期T=
s=2
s,而g=4π2=9.7
m/s2.
(3)设摆线底端到摆球重心的距离为r,则有T1=2π,T2=2π,由两式得g=4π2.
答案:(1)C (2)2.125 98.49 100.0 2 9.7 (3)4π2
13.解析:(1)单摆周期T=2π,单摆完成n次全振动所用的时间为t,可得T=,联立可得g=.测量周期时,摆球振动过程中摆线略微变长,则摆长的测量值偏小,故测得的重力加速度偏小.
(2)根据题图所示的v-t图线,可知该单摆的周期T=2.0
s.
(3)根据T=2π得T2=·L
根据表达式可知图线的斜率k==4.04
s2/m
解得g=9.76
m/s2
答案:(1) 偏小 (2)2.0 (3)9.76
14.解析:(1)由题图知,在计时开始的时刻振子恰好以沿x轴正方向的速度通过平衡位置,此时弹簧振子有最大动能,随着时间的延长,速度不断减小,而位移逐渐增大,经T,即1
s,其位移达到最大,此时弹性势能最大.
(2)由题图知,t=2
s时,振子恰好通过平衡位置,此时加速度为零;随着时间的延长,位移不断增大,加速度也变大,速度不断减小,动能不断减小,弹性势能逐渐增大;当t=3
s时,加速度达到最大,速度等于零,动能等于零,弹性势能达到最大值.
(3)振子经一个周期,位移为零,路程为4×5
cm=20
cm,前100
s刚好经过了25个周期,所以前100
s内振子位移x=0,振子通过的路程s=20
cm×25=500
cm=5
m.
答案:(1)1
s (2)见解析 (3)0 5
m
15.解析:(1)根据振幅的定义,可知振幅A=5
cm;根据周期的定义可知,周期T=2×1
s=2
s.
(2)因为ω=,所以ω=π.
又据题意知t=0时,x=5
cm.因为简谐运动的表达式是x=Asin(ωt+φ),把上面已知数据代入得φ=,所以该振动的表达式x=5sin
cm.
(3)如果从小球经过平衡位置向左运动开始计时,则t=0时,x=0,此后位移负值变大,所以小球的位移表达式x=-5sin(πt)
cm.
答案:(1)5
cm 2
s (2)x=5sin
cm
(3)x=-5sin(πt)
cm
16.解析:(1)由题图(乙)得小滑块做简谐振动的周期T=
s
由T=2π得R==0.1
m.
(2)在最高点A有Fmin=mgcos
θ
在最低点B有Fmax-mg=m
从A到B,滑块机械能守恒mgR(1-cos
θ)=mv2
解得m=0.05
kg.
(3)滑块机械能守恒E=mv2=R(Fmax-mg)=5×10-4
J.
答案:(1)0.1
m (2)0.05
kg (3)5×10-4
J
PAGE
-
9
-
时间:60分钟 满分:100分
一、选择题(本题共10个小题,1~6题为单项选择题,7~10题为多项选择题,每小题4分,共40分.)
1.关于简谐运动的回复力F=-kx的含义,下列说法正确的是( )
A.k是弹簧的劲度系数,x是弹簧的长度
B.k是回复力跟位移的比值,x是做简谐运动的物体离开平衡位置的位移
C.根据k=-,可以认为k与F成正比
D.表达式中的“-”号表示F始终阻碍物体的运动
2.
如图所示是某振子做简谐运动的图象,以下说法中正确的是( )
A.因为振动图象可由实验直接得到,所以图象就是振子实际运动的轨迹
B.振动图象反映的是振子位移随时间变化的规律,并不是振子运动的实际轨迹
C.振子在B位置的位移就是曲线BC的长度
D.振子运动到B点时的速度方向即为该点的切线方向
3.关于做简谐运动的单摆,下列说法正确的是( )
A.摆球经过平衡位置时所受合力为零
B.摆球所受合力的大小跟摆球相对平衡位置的位移大小成正比
C.只有在最高点时,回复力才等于重力和摆线拉力的合力
D.摆球在任意位置处,回复力都不等于重力和摆线拉力的合力
4.弹簧劲度系数为20
N/cm的水平弹簧振子,它的振动图象如图所示,下列说法正确的是( )
A.A点对应的时刻振子所受的弹力大小为0.5
N,方向指向x轴的负方向
B.A点对应的时刻振子的速度方向指向x轴的正方向
C.在0~4
s内振子做了1.75次全振动
D.在0~4
s内振子通过的路程为3.5
cm,位移为0
5.如图所示,图甲为以O点为平衡位置,在A、B两点间做简谐运动的弹簧振子,图乙为该弹簧振子的振动图象,由图可知下列说法中正确的是( )
A.在t=0.2
s时,弹簧振子可能运动到B位置
B.在t=0.1
s与t=0.3
s两个时刻,弹簧振子的速度相同
C.从t=0到t=0.2
s的时间内,弹簧振子的动能持续地增加
D.在t=0.2
s与t=0.6
s两个时刻,弹簧振子的加速度相同
6.
一个做简谐运动的质点,先后以同样大小的速度通过相距10
cm的A、B两点,且由A到B的过程中速度方向不变,历时0.5
s(如图).过B点后再经过t=0.5
s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是( )
A.0.5
s B.1.0
s
C.2.0
s
D.4.0
s
7.一个弹簧振子的振幅是A,若在Δt的时间内物体运动的路程是s,则下列关系中可能正确的是(包括一定正确的)( )
A.Δt=2T,s=8A
B.Δt=,s=2A
C.Δt=,s=2A
D.Δt=,s>A
8.一弹簧振子在水平方向上做简谐运动,其位移x与时间t的关系曲线如图所示,在t=3.2
s时,振子的( )
A.速度正在增大,加速度沿正方向且正在减小
B.速度正在减小,回复力沿负方向且正在增大
C.动能正在转化为势能
D.势能正在转化为动能
9.如图甲所示,一弹簧振子在A、B间振动,取向右为正方向,振子经过O点时为计时时刻,其振动的x-t图象如图乙所示,则下列说法中正确的是( )
A.t2时刻振子在A点
B.t2时刻振子在B点
C.在t1~t2时间内,振子的位移在增大
D.在t3~t4时间内,振子的位移在减小
10.如图所示,下列说法正确的是( )
A.振动图象上的A,B两点的速度相同
B.在t=0.1
s和t=0.3
s时,质点的加速度大小相等,方向相反
C.振动图象上A,B两点的速度大小相等,方向相反
D.质点在t=0.2
s和t=0.3
s时的动能相等
二、非选择题(本题共6个小题,共60分)
11.(6分)在“利用沙摆描绘振动图象”的实验中,将细沙倒在漏斗中,在细沙漏出的同时,让沙摆摆动起来,一段时间后,形成的长条形沙堆如图甲所示:两边高且粗,中间低且细.
(1)如果在沙摆摆动的同时匀速拉动下方纸板(纸板上的虚线O1O2位于沙漏静止时的正下方),则一段时间后,形成如图乙所示的曲线沙堆.分析可知,曲线沙堆在与虚线O1O2垂直距离________(选填“近”或“远”)的位置低且细.
(2)图丙为图乙中纸板上曲线沙堆的俯视图,沿沙摆振动方向建立x轴,沿O1O2方向建立t轴,就利用沙堆曲线得到了沙摆的振动图象,请说明为什么要匀速拉动下方纸板:________________________________________________________________________
________________________________________________________________________.
12.(9分)在“利用单摆测重力加速度”的实验中:
(1)以下做法正确的是( )
A.测量摆长的方法:用刻度尺量出从悬点到摆球间的细线长
B.测量周期时,从小球到达最大振幅位置开始计时,摆球完成50次全振动时,及时截止,然后求出完成一次全振动的时间
C.要保证单摆自始至终在同一竖直平面内摆动
D.单摆摆动时,应注意使它的偏角不小于5°
(2)某同学先用米尺测得摆线长为97.43
cm,用游标卡尺测得摆球直径如图甲所示,为________cm,则单摆的摆长为________cm;然后用停表记录了单摆完成50次全振动所用的时间如图乙所示,为________s,则单摆的周期为________s;当地的重力加速度为g=________m/s2.
(3)实验中,如果摆球密度不均匀,就无法确定重心位置,一位同学设计了一个巧妙的方法不计摆球的半径.具体做法如下:第一次量得悬线长L1,测得振动周期为T1;第二次量得悬线长L2,测得振动周期为T2,由此可推得重力加速度为g=________.
13.(10分)甲、乙两个学习小组分别利用单摆测量重力加速度.
(1)甲组同学采用如图甲所示的实验装置.该组同学先测出悬点到小球球心的距离L,然后用秒表测出单摆完成n次全振动所用的时间t.请写出重力加速度的表达式g=________(用所测物理量表示).在测量摆长后,测量周期时,摆球振动过程中摆线略微变长,这将会导致所测重力加速度的数值________.(选填“偏大”“偏小”或“不变”)
(2)乙组同学在图甲所示装置的基础上再增加一个速度传感器,如图乙所示,将摆球拉开一小角度使其做简谐运动,速度传感器记录了摆球振动过程中速度随时间变化的关系,如图丙所示,由图丙可知,该单摆的周期T=________s.
(3)在多次改变摆线长度测量后,根据实验数据,利用计算机作出T2-L图线,并根据图线拟合得到方程T2=4.04L+0.0035.由此可以得出当地的重力加速度g=________m/s2.(取π2=9.86,结果保留三位有效数字)
14.(10分)如图所示为一弹簧振子的振动图象,求:
(1)从计时开始经多长时间第一次达到弹性势能最大?
(2)在2~3
s这段时间内弹簧振子的加速度、速度、动能和弹性势能各怎样变化?
(3)该振子在前100
s内的总位移是多少?路程是多少?
15.(10分)如图是一弹簧振子,O为平衡位置,B、C为两个极端位置,取向右为正方向,现把小球向右移动5
cm到B点,放手后发现小球经过1
s第一次到达C点,如果从B点放手时开始计时,求:
(1)小球做简谐运动的振幅、周期各是多少?
(2)写出小球运动的位移表达式.
(3)如果从小球经过平衡位置向左运动开始计时,则小球的位移表达式如何?
16.(15分)将一测力传感器连接到计算机上就可以测量快速变化的力.图(甲)表示小滑块(可视为质点)沿固定的光滑半球形容器内壁在竖直平面的A,A′之间来回滑动.A,A′点与O点连线与竖直方向之间夹角θ相等且很小,图(乙)表示滑块对器壁的压力F随时间t变化的曲线,图中t=0为滑块从A点开始运动的时刻.试根据力学规律和题中(包括图中)所给的信息,g取10
m/s2.求:
(1)容器的半径;
(2)小滑块的质量;
(3)滑块运动过程中的机械能.
章末综合检测(第十一章)
1.解析:对弹簧振子来说k为劲度系数,x为质点离开平衡位置位移大小,故A错误;对于其他简谐运动k不是劲度系数,而是一个比例系数,故B正确;该系数由系统本身结构决定,与力F和位移x无关,C错误;“-”只表示回复力与位移反向,回复力有时是动力,D错误.
答案:B
2.解析:振动图象表示位移随时间的变化规律,并不是运动轨迹,B对,A、C错.切线的方向只表示质点的速度方向与规定的正方向相同还是相反,不表示速度的方向.另外由于图象不是质点的运动轨迹,因此切线的方向并不表示速度的方向.
答案:B
3.解析:摆球经过平衡位置时,回复力为零,但由于摆球做圆周运动,经过平衡位置,合力不为零,合力提供向心力,方向指向悬点,A错误;摆球所受回复力由重力沿圆弧切线方向的分力提供,重力沿摆线方向的分力与摆线对摆球的拉力的合力提供向心力,所以摆球所受合力的大小跟摆球相对平衡位置的位移大小不成正比,B错误;根据牛顿第二定律可知,摆球在最大位移处时,速度为零,向心加速度为零,重力沿摆线方向的分力等于摆线对摆球的拉力,回复力才等于重力和摆线拉力的合力,在其他位置时,速度不为零,向心加速度不为零,重力沿摆线方向的分力小于摆线对摆球的拉力,回复力不等于重力和摆线拉力的合力,故C正确,D错误.
答案:C
4.解析:由图可知A点在t轴上方,位移x=0.25
cm,所以弹力F=-kx=-5
N,即弹力大小为5
N,方向指向x轴负方向,A项错误.由图可知A点对应的时刻振子的速度方向指向x轴的正方向,B项正确.由图可看出,t=0
s、t=2
s、t=4
s时刻振子的位移都是最大的,且都在t轴的上方,在0~4
s内完成两次全振动,C项错误.由于t=0时刻和t=4
s时刻振子都在最大位移处,所以在0~4
s内振子的位移为零,又由于振幅为0.5
cm,在0~4
s内振子完成了2次全振动,所以在这段时间内振子通过的路程为2×4×0.5
cm=4
cm,故D项错误.
答案:B
5.解析:t=0.2
s时,振子的位移为正的最大,但由于没有规定正方向,所以此时振子的位置可能在A点也可能在B点,A正确.t=0.1
s时速度为正,t=0.3
s时速度为负,两者方向相反,B错.从t=0到t=0.2
s的时间内,弹簧振子远离平衡位置,速度减小,动能减小,C错.t=0.2
s与t=0.6
s两个时刻,位移大小相等,方向相反,故加速度大小相等,方向相反,D错.
答案:A
6.解析:根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧.质点从平衡位置O向右运动到B的时间应为tOB=×0.5
s=0.25
s.质点从B向右到达右方极端位置(设为D)的时间tBD=×0.5
s=0.25
s.所以质点从O到D的时间tOD=T=0.25
s+0.25
s=0.5
s.所以T=2.0
s,C对.
答案:C
7.解析:因每个全振动所通过的路程为4A,每半个周期所通过的路程为2A,故A、B正确,C错误,又因振幅为振子的最大位移,而s为时的路程,故s有可能大于A,故D正确.
答案:ABD
8.解析:结合简谐运动的振动图象分析物理量的变化,由图可知,当=3.2
s时振子正在向最大位移处运动,位移为正向,速度正在减小,加速度和回复力沿负方向且正在增大,振子动能减小,弹簧弹性势能增大,动能正在转化为势能,B、C正确.A、D错误.
答案:BC
9.解析:振子在A点和B点时位移最大,由于取向右为正方向,所以振子运动到A点有正向最大位移,在B点有负向最大位移,则t2时刻,振子在A点,t4时刻,振子在B点,故选项A正确,B错误;振子的位移是以平衡位置为起点,所以在t1~t2和t3~t4时间内振子的位移都在增大,故选项C正确,D错误.
答案:AC
10.解析:A,B两点位移相同,但在A点时质点正远离平衡位置,在B点时质点正衡位置,所以图象上A,B两点速度大小相等,方向相反,选项A错误,C正确;t=0.1
s和t=0.3
s时,质点分别处在正、负最大位移处,加速度为最大值,但方向相反,选项B正确;t=0.2
s时,质点速度最大,动能最大,
t=0.3
s时,质点速度最小为零,动能为零,选项D错误.
答案:BC
11.解析:(1)单摆在摆动的过程中是变速运动,经过平衡位置的速度最大,最大位移处的速度为0;在相同的时间内漏下的沙子一样多,但在平衡位置附近速度大,相同时间内经过的距离长,故漏下的沙子低且细;
(2)只有拉动木板的速度恒定时,木板的位移与时间成正比,这样建立的位移轴才可以代表时间轴.
答案:(1)近 (2)只有拉动木板的速度恒定时,木板的位移与时间成正比,这样建立的位移轴才可以代表时间轴
12.解析:(1)单摆的摆长应为摆线长度加上摆球的半径,A选项错误;以摆球通过平衡位置(速度最大处)为计时起点可以减小计时误差,B选项错误;单摆摆动时应保持在同一竖直平面内,C选项正确;单摆振动过程中偏角应不超过5°,D选项错误.
(2)摆球直径为(21+5×0.05)
mm
=21.25
mm=2.125
cm.
摆长l=(97.43+)
cm=98.49
cm.
停表读数为(90+10.0)
s=100.0
s.
周期T=
s=2
s,而g=4π2=9.7
m/s2.
(3)设摆线底端到摆球重心的距离为r,则有T1=2π,T2=2π,由两式得g=4π2.
答案:(1)C (2)2.125 98.49 100.0 2 9.7 (3)4π2
13.解析:(1)单摆周期T=2π,单摆完成n次全振动所用的时间为t,可得T=,联立可得g=.测量周期时,摆球振动过程中摆线略微变长,则摆长的测量值偏小,故测得的重力加速度偏小.
(2)根据题图所示的v-t图线,可知该单摆的周期T=2.0
s.
(3)根据T=2π得T2=·L
根据表达式可知图线的斜率k==4.04
s2/m
解得g=9.76
m/s2
答案:(1) 偏小 (2)2.0 (3)9.76
14.解析:(1)由题图知,在计时开始的时刻振子恰好以沿x轴正方向的速度通过平衡位置,此时弹簧振子有最大动能,随着时间的延长,速度不断减小,而位移逐渐增大,经T,即1
s,其位移达到最大,此时弹性势能最大.
(2)由题图知,t=2
s时,振子恰好通过平衡位置,此时加速度为零;随着时间的延长,位移不断增大,加速度也变大,速度不断减小,动能不断减小,弹性势能逐渐增大;当t=3
s时,加速度达到最大,速度等于零,动能等于零,弹性势能达到最大值.
(3)振子经一个周期,位移为零,路程为4×5
cm=20
cm,前100
s刚好经过了25个周期,所以前100
s内振子位移x=0,振子通过的路程s=20
cm×25=500
cm=5
m.
答案:(1)1
s (2)见解析 (3)0 5
m
15.解析:(1)根据振幅的定义,可知振幅A=5
cm;根据周期的定义可知,周期T=2×1
s=2
s.
(2)因为ω=,所以ω=π.
又据题意知t=0时,x=5
cm.因为简谐运动的表达式是x=Asin(ωt+φ),把上面已知数据代入得φ=,所以该振动的表达式x=5sin
cm.
(3)如果从小球经过平衡位置向左运动开始计时,则t=0时,x=0,此后位移负值变大,所以小球的位移表达式x=-5sin(πt)
cm.
答案:(1)5
cm 2
s (2)x=5sin
cm
(3)x=-5sin(πt)
cm
16.解析:(1)由题图(乙)得小滑块做简谐振动的周期T=
s
由T=2π得R==0.1
m.
(2)在最高点A有Fmin=mgcos
θ
在最低点B有Fmax-mg=m
从A到B,滑块机械能守恒mgR(1-cos
θ)=mv2
解得m=0.05
kg.
(3)滑块机械能守恒E=mv2=R(Fmax-mg)=5×10-4
J.
答案:(1)0.1
m (2)0.05
kg (3)5×10-4
J
PAGE
-
9
-
