人教版 高一物理 必修一 第三章:3.4 力的合成(共27张PPT)
文档属性
| 名称 | 人教版 高一物理 必修一 第三章:3.4 力的合成(共27张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
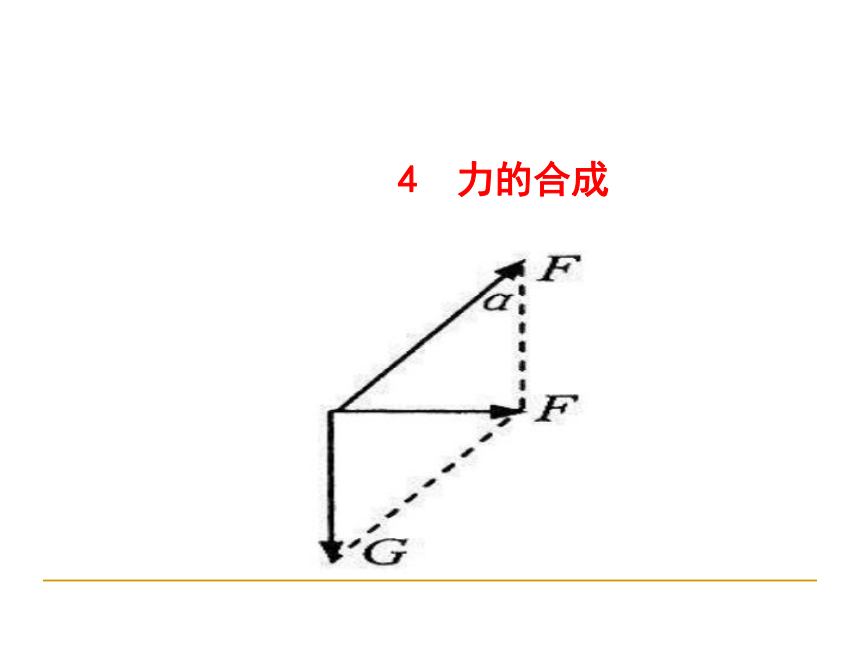
4
力的合成
F1
F2
G
F
G
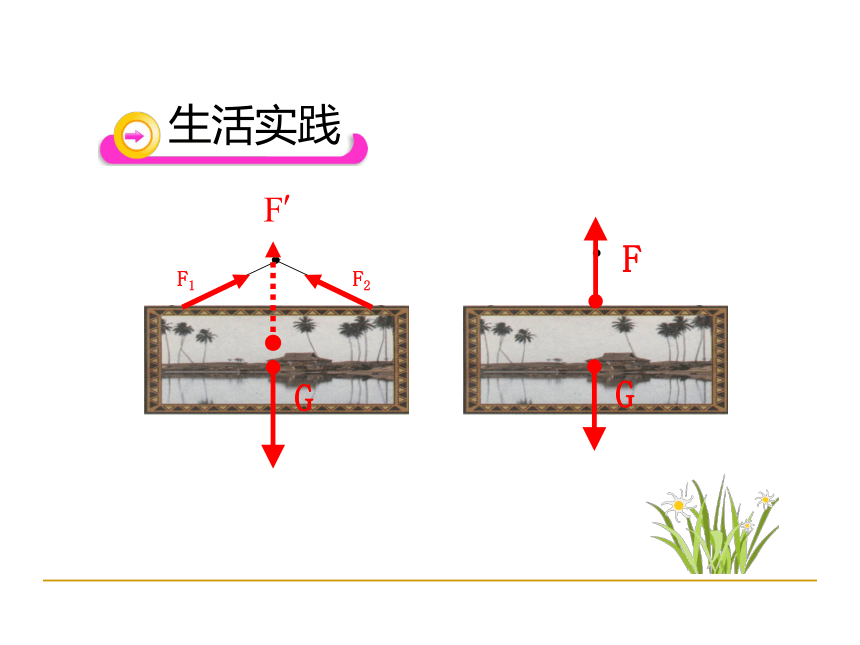
生活实践
F1
F2
G
F
G
F
1
F
2
F
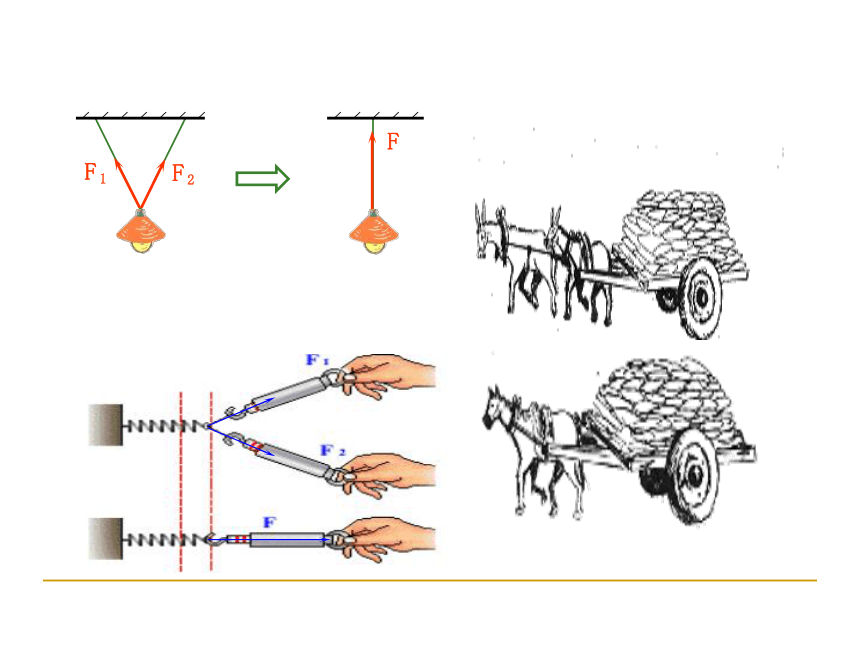
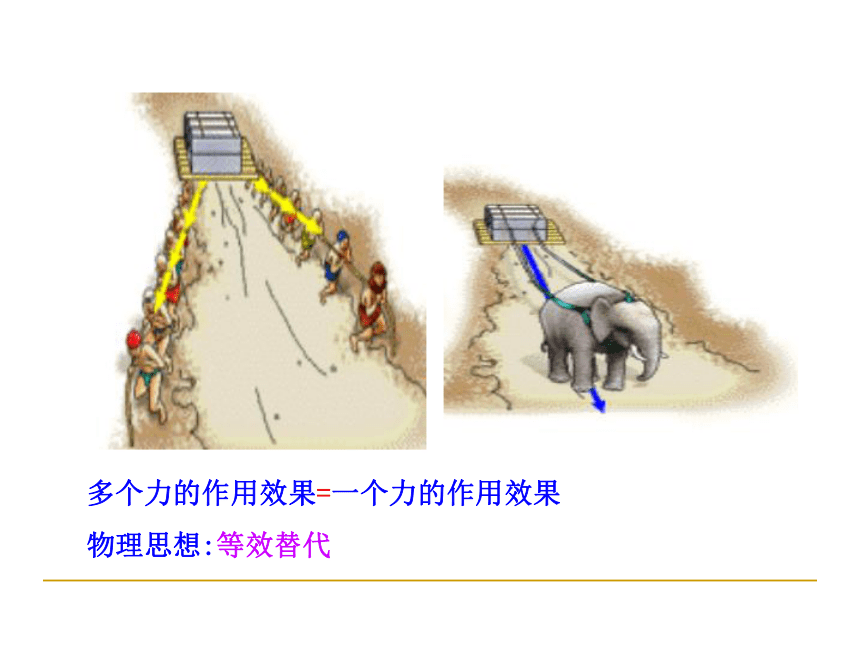
多个力的作用效果=一个力的作用效果
物理思想:等效替代
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的共同效果相同,这个力就叫做那几个力的合力。原来的几个力叫做这个力的分力。
1、合力
:
说明:在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。而不是物体又多受了一个合力。
求几个力的合力的过程或方法,叫做力的合成.
2、力的合成:
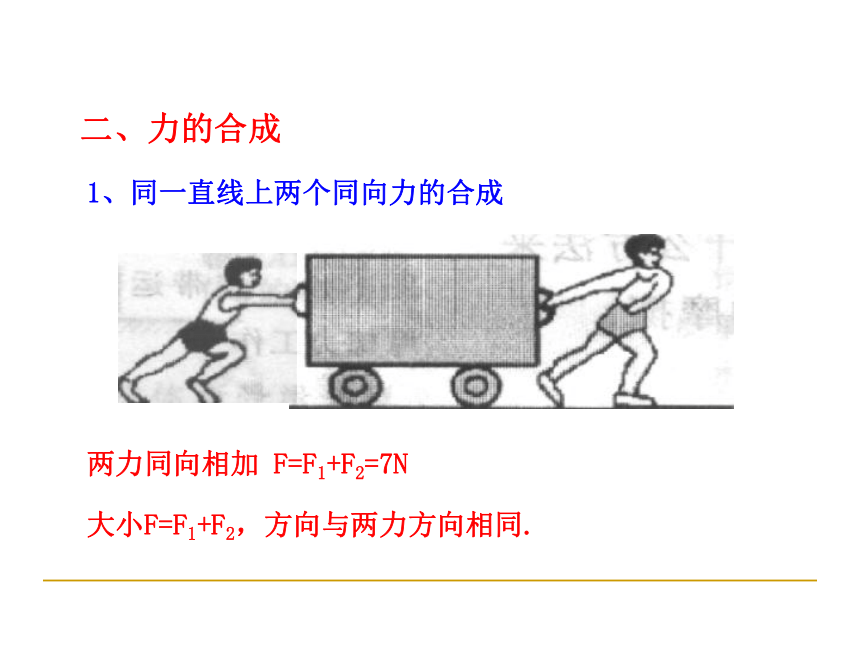
二、力的合成
两力同向相加
F=F1+F2=7N
大小F=F1+F2,方向与两力方向相同.
1、同一直线上两个同向力的合成
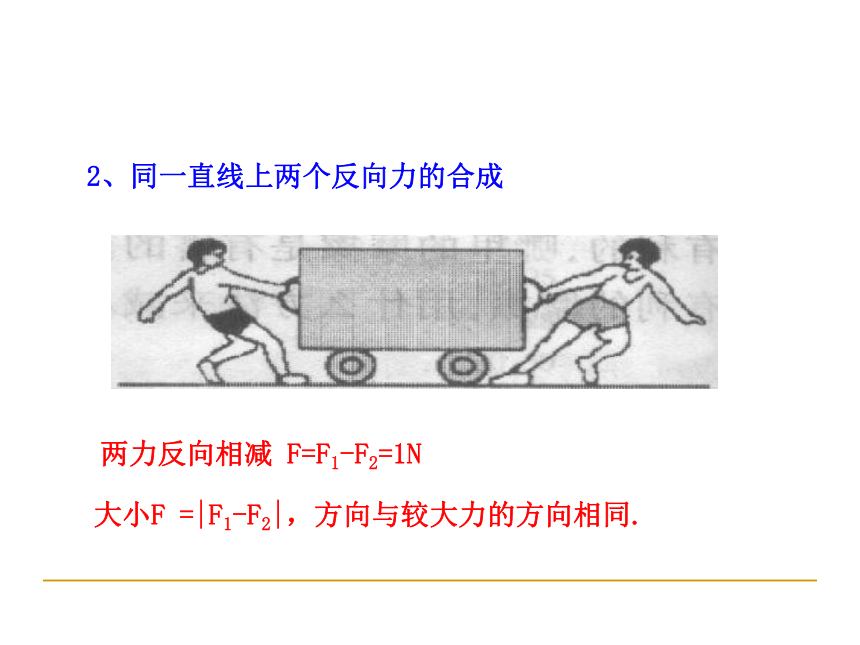
大小F
=|F1-F2|,方向与较大力的方向相同.
两力反向相减
F=F1-F2=1N
2、同一直线上两个反向力的合成
不在同一直线上的两个力怎样求合力?
提出猜想
制定计划与设计实验
实验目的:探究求合力的方法。
实验原理:合力的作用效果与几个分力的作用效果相同。
实验准备:
1、用什么方法表示分力与合力的大小和方向?
2、怎样表明橡皮筋在一个力F的作用下作用效果与两个力F1、F2的共同作用效果相同?
3、实验过程中需要记录哪些实验数据?
实验器材:粘好白纸的方木板、弹簧测力计2个、橡皮筋1条、细绳、刻度尺。
丙
把橡皮条一端A固定在铺有白纸、水平放置的木板上,在橡皮条的另一端B结上两个细绳套。如图甲所示,用两个弹簧测力计通过细绳套拉橡皮条的B端,使橡皮条伸长到O点,记下O点的位置、两细绳所在的直线和两弹簧测力计的示数,这样就确定了两个分力的大小和方向;如图乙所示,用一个弹簧测力计通过细绳套拉橡皮条的B端,使它仍伸长到O点的位置,记下细绳所在的直线和弹簧测力计示数,这个力的作用效果与两个力同时作用时是相同的。
1、求两个力的合力时,以表示这两个力的线段为邻边作平行四边形,夹在两邻边之间的对角线就表示合力的大小和方向,这个法则叫平行四边形定则。
F1
O
F2
实验结论总结
2、平行四边形定则是矢量合成的通用法则。
【例题】气球在空中受到的空气浮力竖直向上,大小为4N,同时受到水平方向的风力作用,大小为3N。求气球受到的浮力与风力的合力。
1、图解法(即力的图示法)求合力
2、计算法求合力
1、图解法(即力的图示法)求合力。
解:选定一个合适的标度,如用一个单位长度表示1N,用O点代表气球,作出气球所受两个力的图示,如图所示。以F1、F2为邻边作平行四边形,作出表示合力F的对角线OF,用刻度尺量出对角线的长,约为5个单位长度,可求得合力的大小约为F=5×1N=5N
用量角器量出合力F与竖直方向的夹角为37.00°
2、计算法求合力
解:根据平行四边形定则作出下图:
F1
F2
F合
θ
由直角三角形可得
方向:与竖直方向夹
角为θ且
两个分力大小一定时,合力的大小随它们之间的夹角是怎样变化的?你能确定合力的取值范围吗?
思考与讨论
三、合力与分力的大小关系
在两个分力F1、F2大小不变的情况下,两个分力的夹角越大,合力越小。
1、当两个分力方向相同时(夹角为00)
合力最大,F=F1
+
F2
合力与分力方向相同;
2、当两个分力方向相反时(夹角为1800)
合力最小,F=︱F1
-
F2︱
合力与分力F1
、F2中较大的方向相同。
3、合力大小范围
︱F1
-
F2︱
≤
F
≤
F1
+
F2
4、合力可能大于、等于、小于任一分力.
三个及三个以上力的合成的方法
先求两个力的合力,再求出这个合力与第三个力的合力,……直到把所有力合为一个力,得到合力。
F1
F2
F3
F4
F12
F123
F1234
共点力:
如果一个物体受两个或多个力作用,这些力都作用在物体上的同一点,或者虽不作用在同一点上,但它们的延长线相交于同一点,这几个力叫做共点力。
力的合成的平行四边形法则,只适用于共点力。
1.下列关于合力与分力的叙述中正确的是(
)
A.合力的大小一定大于每一分力的大小。
B.合力可以同时垂直于每一分力。
C.合力与分力间是一种等效替代关系,不能同时考查它们的作用效果。
D.若两个分力的大小不变,则合力的大小也不会变化
C
2.F1与F2为作用在同一物体上的两个力,F1=10N,F2=
8N,它们的合力大小可能是(
)
A.19N
B.18N
C.10N
D.2N
3.有两个大小相等的共点力F1和F2,当它们间的夹角为90°时合力为F,则当它们间的夹角为120°时,合力的大小为(
)
A.2F
B.
C.
F
D.
BCD
B
4.如图所示,一木块放在水平桌面上,受水平方向的推力F1和F2的作用,但木块处于静止状态,F1=10N,F2=2N,则木块受到合力F合和F1和F2的合力F的大小,方向是(
)
A.
F合=0;
F
=8N,方向向右
B.
F合=0,F=0
C.
F合=10N,方向向左;F=8N,方向向左
D.
F合=10N,方向向左;F=12N,方向向右
A
2.一个定则:
3.两种方法
1.一种思想:等效替代
计算法:准确
平行四边形定则
适用所有矢量的合成和分解
图解法:直观、误差大
4
力的合成
F1
F2
G
F
G
生活实践
F1
F2
G
F
G
F
1
F
2
F
多个力的作用效果=一个力的作用效果
物理思想:等效替代
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的共同效果相同,这个力就叫做那几个力的合力。原来的几个力叫做这个力的分力。
1、合力
:
说明:在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。而不是物体又多受了一个合力。
求几个力的合力的过程或方法,叫做力的合成.
2、力的合成:
二、力的合成
两力同向相加
F=F1+F2=7N
大小F=F1+F2,方向与两力方向相同.
1、同一直线上两个同向力的合成
大小F
=|F1-F2|,方向与较大力的方向相同.
两力反向相减
F=F1-F2=1N
2、同一直线上两个反向力的合成
不在同一直线上的两个力怎样求合力?
提出猜想
制定计划与设计实验
实验目的:探究求合力的方法。
实验原理:合力的作用效果与几个分力的作用效果相同。
实验准备:
1、用什么方法表示分力与合力的大小和方向?
2、怎样表明橡皮筋在一个力F的作用下作用效果与两个力F1、F2的共同作用效果相同?
3、实验过程中需要记录哪些实验数据?
实验器材:粘好白纸的方木板、弹簧测力计2个、橡皮筋1条、细绳、刻度尺。
丙
把橡皮条一端A固定在铺有白纸、水平放置的木板上,在橡皮条的另一端B结上两个细绳套。如图甲所示,用两个弹簧测力计通过细绳套拉橡皮条的B端,使橡皮条伸长到O点,记下O点的位置、两细绳所在的直线和两弹簧测力计的示数,这样就确定了两个分力的大小和方向;如图乙所示,用一个弹簧测力计通过细绳套拉橡皮条的B端,使它仍伸长到O点的位置,记下细绳所在的直线和弹簧测力计示数,这个力的作用效果与两个力同时作用时是相同的。
1、求两个力的合力时,以表示这两个力的线段为邻边作平行四边形,夹在两邻边之间的对角线就表示合力的大小和方向,这个法则叫平行四边形定则。
F1
O
F2
实验结论总结
2、平行四边形定则是矢量合成的通用法则。
【例题】气球在空中受到的空气浮力竖直向上,大小为4N,同时受到水平方向的风力作用,大小为3N。求气球受到的浮力与风力的合力。
1、图解法(即力的图示法)求合力
2、计算法求合力
1、图解法(即力的图示法)求合力。
解:选定一个合适的标度,如用一个单位长度表示1N,用O点代表气球,作出气球所受两个力的图示,如图所示。以F1、F2为邻边作平行四边形,作出表示合力F的对角线OF,用刻度尺量出对角线的长,约为5个单位长度,可求得合力的大小约为F=5×1N=5N
用量角器量出合力F与竖直方向的夹角为37.00°
2、计算法求合力
解:根据平行四边形定则作出下图:
F1
F2
F合
θ
由直角三角形可得
方向:与竖直方向夹
角为θ且
两个分力大小一定时,合力的大小随它们之间的夹角是怎样变化的?你能确定合力的取值范围吗?
思考与讨论
三、合力与分力的大小关系
在两个分力F1、F2大小不变的情况下,两个分力的夹角越大,合力越小。
1、当两个分力方向相同时(夹角为00)
合力最大,F=F1
+
F2
合力与分力方向相同;
2、当两个分力方向相反时(夹角为1800)
合力最小,F=︱F1
-
F2︱
合力与分力F1
、F2中较大的方向相同。
3、合力大小范围
︱F1
-
F2︱
≤
F
≤
F1
+
F2
4、合力可能大于、等于、小于任一分力.
三个及三个以上力的合成的方法
先求两个力的合力,再求出这个合力与第三个力的合力,……直到把所有力合为一个力,得到合力。
F1
F2
F3
F4
F12
F123
F1234
共点力:
如果一个物体受两个或多个力作用,这些力都作用在物体上的同一点,或者虽不作用在同一点上,但它们的延长线相交于同一点,这几个力叫做共点力。
力的合成的平行四边形法则,只适用于共点力。
1.下列关于合力与分力的叙述中正确的是(
)
A.合力的大小一定大于每一分力的大小。
B.合力可以同时垂直于每一分力。
C.合力与分力间是一种等效替代关系,不能同时考查它们的作用效果。
D.若两个分力的大小不变,则合力的大小也不会变化
C
2.F1与F2为作用在同一物体上的两个力,F1=10N,F2=
8N,它们的合力大小可能是(
)
A.19N
B.18N
C.10N
D.2N
3.有两个大小相等的共点力F1和F2,当它们间的夹角为90°时合力为F,则当它们间的夹角为120°时,合力的大小为(
)
A.2F
B.
C.
F
D.
BCD
B
4.如图所示,一木块放在水平桌面上,受水平方向的推力F1和F2的作用,但木块处于静止状态,F1=10N,F2=2N,则木块受到合力F合和F1和F2的合力F的大小,方向是(
)
A.
F合=0;
F
=8N,方向向右
B.
F合=0,F=0
C.
F合=10N,方向向左;F=8N,方向向左
D.
F合=10N,方向向左;F=12N,方向向右
A
2.一个定则:
3.两种方法
1.一种思想:等效替代
计算法:准确
平行四边形定则
适用所有矢量的合成和分解
图解法:直观、误差大
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
