五年级上册数学导学案-04三角形的面积计算 苏教版
文档属性
| 名称 | 五年级上册数学导学案-04三角形的面积计算 苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 57.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 15:10:23 | ||
图片预览

文档简介
五上数学导学案
第二单元:三角形的面积计算
教学目标:
1、使学生经历操作、观察、填表、讨论、归纳等数学活动,探索并掌握三角形的面积公式,能正确地计算三角形的面积,并应用公式解决简单的实际问题。
2、使学生进一步体会转化方法的价值,培养学生应用已有知识解决新问题的能力,发展学生的空间观念和初步的推理能力。
3、培养学生良好的数学兴趣和探究意识,体验数学的价值。
教学重点:理解并掌握三角形面积的计算公式。
教学难点:理解三角形面积公式的推导过程。
一、预习方向标——“仙”人一步!
⒈阅读课本P9例4,要求出涂色三角形的面积可以这样做:
⑴可以用数方格法求出每个涂色三角形的面积,不满一格的都按半格计算:
图①涂色的三角形:6个整格+4个半格 →S①=_____cm2
图②涂色的三角形:4个整格+___个半格 →S②=_____ cm2
图③涂色的三角形:___个整格+___个半格 →S③=_____ cm2
⑵还可以根据平行四边形的面积求涂色三角形的面积:
图①平行四边形的底是 cm,高是 cm,面积是 cm2,所以图①涂色的三角形面积是 cm2
图②平行四边形的底是 cm,高是 cm,面积是 cm2,所以图②涂色的三角形面积是 cm2
图③平行四边形的底是 cm,高是 cm,面积是 cm2,所以图③涂色的三角形面积是 cm2
我发现:每个图形中空白和涂色三角形的形状、大小完全相同,这样的两个三角形能拼成平行四边形,拼成的平行四边形面积是每个三角形面积的_____倍。
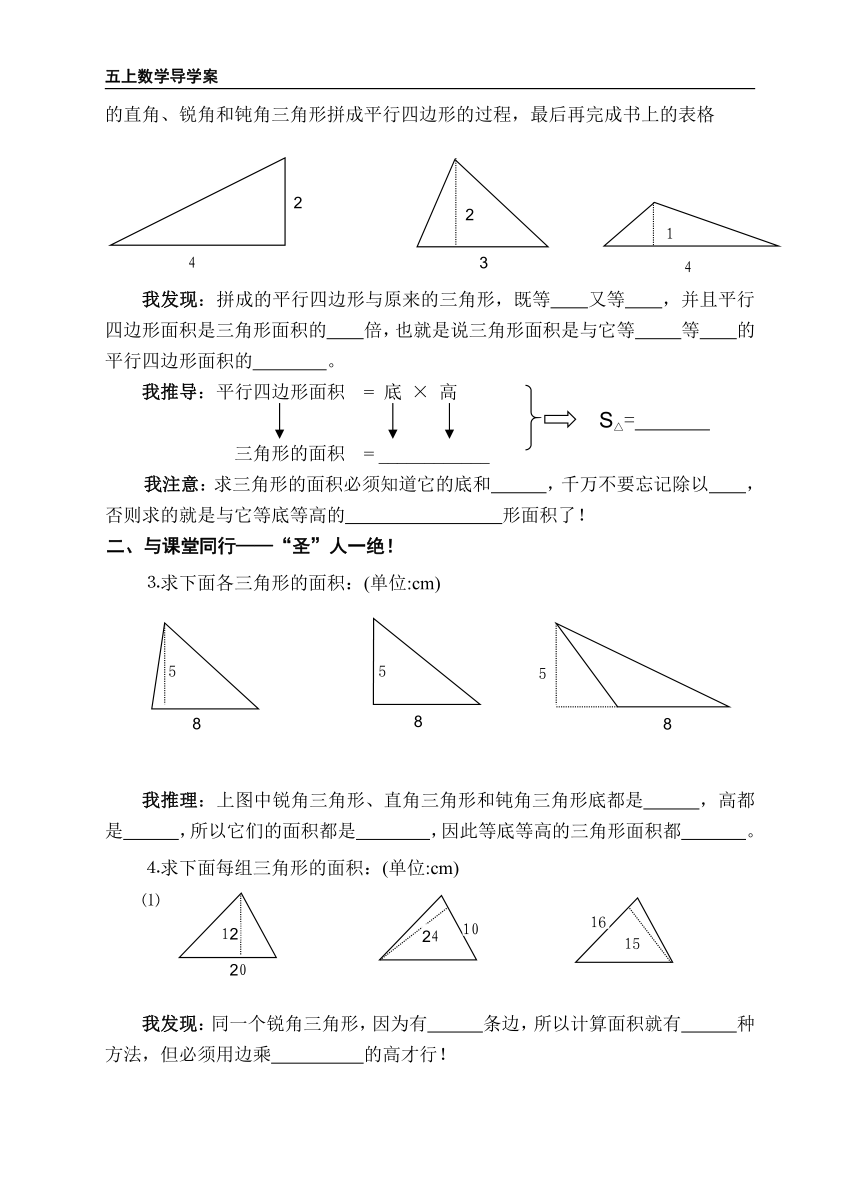
⒉阅读课本P15例5,请拼一拼、量一量,并在下面的图上分别画出两个同样的直角、锐角和钝角三角形拼成平行四边形的过程,最后再完成书上的表格
我发现:拼成的平行四边形与原来的三角形,既等 又等 ,并且平行四边形面积是三角形面积的 倍,也就是说三角形面积是与它等 等 的平行四边形面积的 。
我推导:平行四边形面积 = 底 × 高
三角形的面积 = ____________
我注意:求三角形的面积必须知道它的底和 ,千万不要忘记除以 ,否则求的就是与它等底等高的 形面积了!
二、与课堂同行——“圣”人一绝!
⒊求下面各三角形的面积:(单位:cm)
我推理:上图中锐角三角形、直角三角形和钝角三角形底都是 ,高都是 ,所以它们的面积都是 ,因此等底等高的三角形面积都 。
⒋求下面每组三角形的面积:(单位:cm)
⑴
我发现:同一个锐角三角形,因为有 条边,所以计算面积就有 种方法,但必须用边乘 的高才行!
⑵
我发现:同一个直角三角形,计算它的面积,既可以用两条 边的长度相乘再除以 ,因它这两条 边是互相 的,也可以用 边长乘它对应的 再 。
⑶
我注意:同一个钝角三角形,计算它的面积也有3种方法。不过除了最长边的高在三角形的 面,其余较短的两条边对应的高都在三角形的 面。千万要注意哟!
三、当日练兵场——“快”人一刻!
底 高 三角形面积 平行四边形面积
12dm 2m
3dm 8m
⒌
⒍⑴一块三角形土地的底是40m,高是25m,这块土地的面积是多少平方米?
⑵一块平行四边形土地的底是40m,高是25m,这块土地的面积是多少平方米?
⒎⑴三角形的面积是120m2,与它等底等高的平行四边形面积是 。
⑵平行四边形面积是120m2,与它等底等高的三角形形面积是 。
⑶一个三角形与一个平行四边形高相等,底也相等。这两个图形的面积和是120 m2,三角形形面积是 ,平行四边形面积是 。
四、挑战陈景润——“悠”进一步!
⒏⑴一个三角形,底是20cm,是高的4倍。这个三角形的面积是多少?
⑵一个三角形,底是20cm,比高的4倍少4cm。这个三角形的面积是多少?
⒐⑴一个直角三角形,三条边的长度分别是6dm、8dm和10dm。这个三角形的面积是多少?
⑵一个等腰三角形,有两条边长分别是20cm和50cm。经测量三条高中有一条高是48cm。这个三角形的面积是多少?
⒑请画出与△ABC面积相等的锐角三角形、直角三角形和钝角三角形各一个,并请仔细观察,你有什么发现?
⒒⑴画与△ABC高相等、面积也相等的平行四边形,它们的底有什么关系?
⑵画与△ABC底相等、面积也相等的平行四边形,它们的高有什么关系?
第二单元:三角形的面积计算
教学目标:
1、使学生经历操作、观察、填表、讨论、归纳等数学活动,探索并掌握三角形的面积公式,能正确地计算三角形的面积,并应用公式解决简单的实际问题。
2、使学生进一步体会转化方法的价值,培养学生应用已有知识解决新问题的能力,发展学生的空间观念和初步的推理能力。
3、培养学生良好的数学兴趣和探究意识,体验数学的价值。
教学重点:理解并掌握三角形面积的计算公式。
教学难点:理解三角形面积公式的推导过程。
一、预习方向标——“仙”人一步!
⒈阅读课本P9例4,要求出涂色三角形的面积可以这样做:
⑴可以用数方格法求出每个涂色三角形的面积,不满一格的都按半格计算:
图①涂色的三角形:6个整格+4个半格 →S①=_____cm2
图②涂色的三角形:4个整格+___个半格 →S②=_____ cm2
图③涂色的三角形:___个整格+___个半格 →S③=_____ cm2
⑵还可以根据平行四边形的面积求涂色三角形的面积:
图①平行四边形的底是 cm,高是 cm,面积是 cm2,所以图①涂色的三角形面积是 cm2
图②平行四边形的底是 cm,高是 cm,面积是 cm2,所以图②涂色的三角形面积是 cm2
图③平行四边形的底是 cm,高是 cm,面积是 cm2,所以图③涂色的三角形面积是 cm2
我发现:每个图形中空白和涂色三角形的形状、大小完全相同,这样的两个三角形能拼成平行四边形,拼成的平行四边形面积是每个三角形面积的_____倍。
⒉阅读课本P15例5,请拼一拼、量一量,并在下面的图上分别画出两个同样的直角、锐角和钝角三角形拼成平行四边形的过程,最后再完成书上的表格
我发现:拼成的平行四边形与原来的三角形,既等 又等 ,并且平行四边形面积是三角形面积的 倍,也就是说三角形面积是与它等 等 的平行四边形面积的 。
我推导:平行四边形面积 = 底 × 高
三角形的面积 = ____________
我注意:求三角形的面积必须知道它的底和 ,千万不要忘记除以 ,否则求的就是与它等底等高的 形面积了!
二、与课堂同行——“圣”人一绝!
⒊求下面各三角形的面积:(单位:cm)
我推理:上图中锐角三角形、直角三角形和钝角三角形底都是 ,高都是 ,所以它们的面积都是 ,因此等底等高的三角形面积都 。
⒋求下面每组三角形的面积:(单位:cm)
⑴
我发现:同一个锐角三角形,因为有 条边,所以计算面积就有 种方法,但必须用边乘 的高才行!
⑵
我发现:同一个直角三角形,计算它的面积,既可以用两条 边的长度相乘再除以 ,因它这两条 边是互相 的,也可以用 边长乘它对应的 再 。
⑶
我注意:同一个钝角三角形,计算它的面积也有3种方法。不过除了最长边的高在三角形的 面,其余较短的两条边对应的高都在三角形的 面。千万要注意哟!
三、当日练兵场——“快”人一刻!
底 高 三角形面积 平行四边形面积
12dm 2m
3dm 8m
⒌
⒍⑴一块三角形土地的底是40m,高是25m,这块土地的面积是多少平方米?
⑵一块平行四边形土地的底是40m,高是25m,这块土地的面积是多少平方米?
⒎⑴三角形的面积是120m2,与它等底等高的平行四边形面积是 。
⑵平行四边形面积是120m2,与它等底等高的三角形形面积是 。
⑶一个三角形与一个平行四边形高相等,底也相等。这两个图形的面积和是120 m2,三角形形面积是 ,平行四边形面积是 。
四、挑战陈景润——“悠”进一步!
⒏⑴一个三角形,底是20cm,是高的4倍。这个三角形的面积是多少?
⑵一个三角形,底是20cm,比高的4倍少4cm。这个三角形的面积是多少?
⒐⑴一个直角三角形,三条边的长度分别是6dm、8dm和10dm。这个三角形的面积是多少?
⑵一个等腰三角形,有两条边长分别是20cm和50cm。经测量三条高中有一条高是48cm。这个三角形的面积是多少?
⒑请画出与△ABC面积相等的锐角三角形、直角三角形和钝角三角形各一个,并请仔细观察,你有什么发现?
⒒⑴画与△ABC高相等、面积也相等的平行四边形,它们的底有什么关系?
⑵画与△ABC底相等、面积也相等的平行四边形,它们的高有什么关系?
