五年级上册数学导学案-05 平行四边形和三角形练习 苏教版
文档属性
| 名称 | 五年级上册数学导学案-05 平行四边形和三角形练习 苏教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 60.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览


文档简介
五上数学导学案
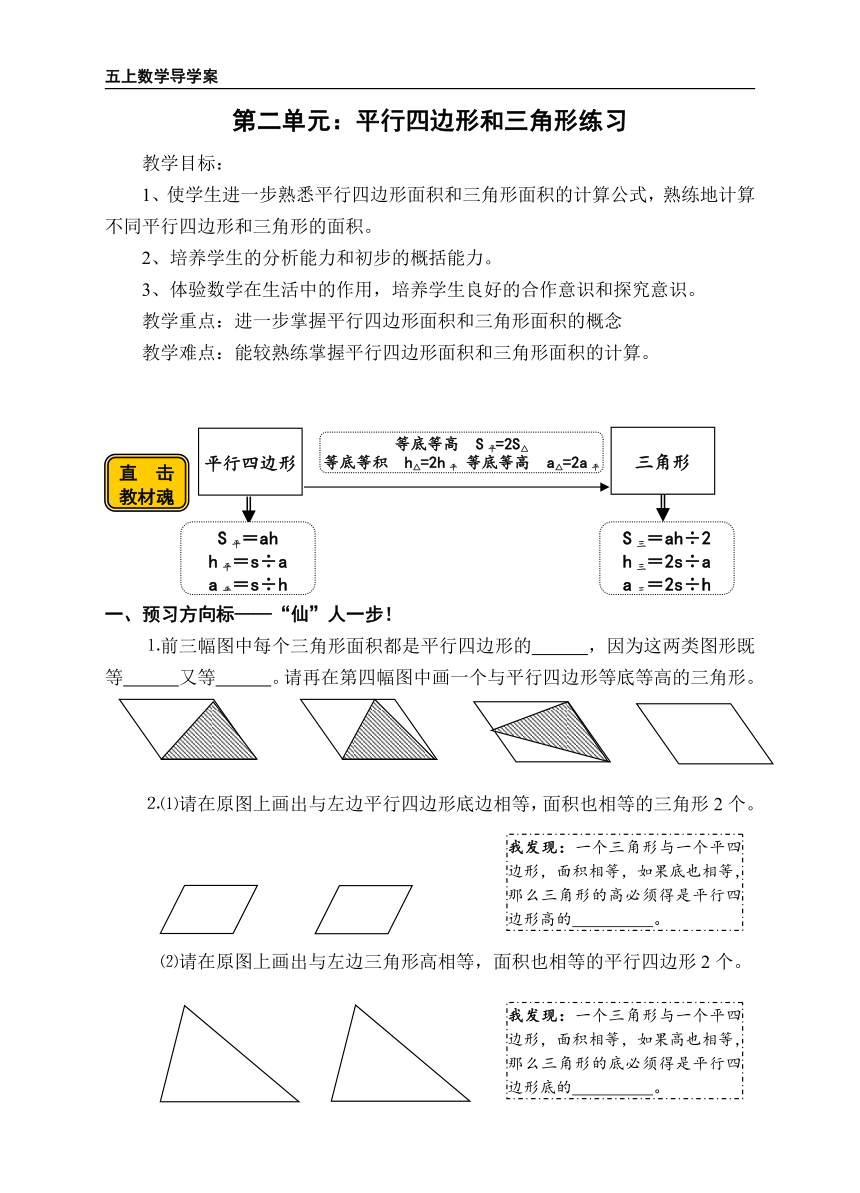
第二单元:平行四边形和三角形练习
教学目标:
1、使学生进一步熟悉平行四边形面积和三角形面积的计算公式,熟练地计算不同平行四边形和三角形的面积。
2、培养学生的分析能力和初步的概括能力。
3、体验数学在生活中的作用,培养学生良好的合作意识和探究意识。
教学重点:进一步掌握平行四边形面积和三角形面积的概念
教学难点:能较熟练掌握平行四边形面积和三角形面积的计算。
一、预习方向标——“仙”人一步!
⒈前三幅图中每个三角形面积都是平行四边形的 ,因为这两类图形既等 又等 。请再在第四幅图中画一个与平行四边形等底等高的三角形。
⒉⑴请在原图上画出与左边平行四边形底边相等,面积也相等的三角形2个。
⑵请在原图上画出与左边三角形高相等,面积也相等的平行四边形2个。
⒉求下面图形的面积:(单位dm)
我发现:求平行四边形面积还是三角形面积必须知道它的 和 的 。
二、与课堂同行——“圣”人一绝!
⒊一个三角形的底是7cm,面积是28cm2,它的高是4cm吗?为什么?
我检验:底7cm,如果高是4cm,那么根据公式,它的面该是7×4÷2=14(cm2),而不是题目所说的28cm2,所以高一定比4cm要大。
我推理:我记得三角形面积公式是由平行四边形面积公式推导出来的,用三角形的底乘高得到的是与它等底等高的 形的面积,再除以2才是三角形本身的面积。那么如果反过来知道三角形的面积和底求高,应该也与平行四边形有关:
⑴28×2=56是指用 个这样的三角形拼成一个与它等 等 的平行四边形,新拼成的平行四边形面积是 cm2;
⑵56÷7得到的是平行四边形的 ,其实也就是原来三角形的 。
我再检验:底7cm,如果高是8cm,那么根据公式它的面积应该是7×8÷2=28(cm2),正好符合题意。
我注意:知道三角形的面积和底,求高,必须先用三角形的面积 ,得到与这个三角形等底等高的 形面积,然后求出它的高,也就是原来三角形的 。
我推理:知道三角形的面积和高,求底,也必须先用三角形的面积 ,得到与这个三角形等底等高的 形面积,然后求出它的底,也就是原来三角形的 。
三角形 平行四边形
底 高 面积 底 高 面积
6dm 3dm
6dm 3dm
8cm
24cm2 8cm
24cm2
25m 100m2
25m 100m2
⒋
我总结:不论是三角形还是平行四边形,与面积相关的是底和高,因此我们只要知道其中的任意两个量就可以求出第三个量:
⑴已知平行四边形底和对应的高,求面积S= ;
已知平行四边形面积和高,求对应的底a= ;
已知平行四边形面积和底,求对应的高h= 。
⑵已知三角形底和对应的高,求面积S= ;
已知三角形面积和高,求对应的底a= ;
已知三角形面积和底,求对应的高h= 。
三、当日练兵场——“快”人一刻!
⒌根据已知条件求解:
⒍一个三角形和一个平行四边形:
⑴如果它们等底等高,平行四边形面积是三角形的 。
⑵如果它们的底边相等、面积也相等,平行四边形的高是三角形的 。
⑶如果它们的高相等、面积也相等,平行四边形的底是三角形的 。
⒎判断
⑴三角形的面积是平行四边形面积的一半。 ( )
⑵三角形的面积不可能与平行四边形面积相等,更不可能比它大。 ( )
⑶平行四边形沿对角线剪开,所得的两个三角形完全一样。 ( )
⑷在面积为40m2的平行四边形中画一个三角形,三角形的面积最大只能20m2。 ( )
⑸用长木条钉成一个长方形框,然后把它拉成一个平行四边形,它的周长、面积都发生了变化。 ( )
四、挑战陈景润——“悠”进一步!
⒏下面都是底25m,对应高16m的平行四边形。请计算出各图中三角形面积。
⒐⑴一个平行四边形,如果底不变,高增加3dm,面积就增加24 dm2;如果高不变,底减少2dm,面积就减少24 dm2。平行四边形原来面积是多少?
⑵一个三角形,如果底不变,高增加3dm,面积就增加24 dm2;如果高不变,底减少2dm,面积就减少24 dm2。三角形原来面积是多少?
⒑⑴一个直角三角形,两条直角边长分别是30m和40m,斜边上的高是24m。这个三角形的周长是多少?
⑵将一个正方形从左上角去掉4cm,面积就减少18cm2。现在剩下的梯形面积是多少?
第二单元:平行四边形和三角形练习
教学目标:
1、使学生进一步熟悉平行四边形面积和三角形面积的计算公式,熟练地计算不同平行四边形和三角形的面积。
2、培养学生的分析能力和初步的概括能力。
3、体验数学在生活中的作用,培养学生良好的合作意识和探究意识。
教学重点:进一步掌握平行四边形面积和三角形面积的概念
教学难点:能较熟练掌握平行四边形面积和三角形面积的计算。
一、预习方向标——“仙”人一步!
⒈前三幅图中每个三角形面积都是平行四边形的 ,因为这两类图形既等 又等 。请再在第四幅图中画一个与平行四边形等底等高的三角形。
⒉⑴请在原图上画出与左边平行四边形底边相等,面积也相等的三角形2个。
⑵请在原图上画出与左边三角形高相等,面积也相等的平行四边形2个。
⒉求下面图形的面积:(单位dm)
我发现:求平行四边形面积还是三角形面积必须知道它的 和 的 。
二、与课堂同行——“圣”人一绝!
⒊一个三角形的底是7cm,面积是28cm2,它的高是4cm吗?为什么?
我检验:底7cm,如果高是4cm,那么根据公式,它的面该是7×4÷2=14(cm2),而不是题目所说的28cm2,所以高一定比4cm要大。
我推理:我记得三角形面积公式是由平行四边形面积公式推导出来的,用三角形的底乘高得到的是与它等底等高的 形的面积,再除以2才是三角形本身的面积。那么如果反过来知道三角形的面积和底求高,应该也与平行四边形有关:
⑴28×2=56是指用 个这样的三角形拼成一个与它等 等 的平行四边形,新拼成的平行四边形面积是 cm2;
⑵56÷7得到的是平行四边形的 ,其实也就是原来三角形的 。
我再检验:底7cm,如果高是8cm,那么根据公式它的面积应该是7×8÷2=28(cm2),正好符合题意。
我注意:知道三角形的面积和底,求高,必须先用三角形的面积 ,得到与这个三角形等底等高的 形面积,然后求出它的高,也就是原来三角形的 。
我推理:知道三角形的面积和高,求底,也必须先用三角形的面积 ,得到与这个三角形等底等高的 形面积,然后求出它的底,也就是原来三角形的 。
三角形 平行四边形
底 高 面积 底 高 面积
6dm 3dm
6dm 3dm
8cm
24cm2 8cm
24cm2
25m 100m2
25m 100m2
⒋
我总结:不论是三角形还是平行四边形,与面积相关的是底和高,因此我们只要知道其中的任意两个量就可以求出第三个量:
⑴已知平行四边形底和对应的高,求面积S= ;
已知平行四边形面积和高,求对应的底a= ;
已知平行四边形面积和底,求对应的高h= 。
⑵已知三角形底和对应的高,求面积S= ;
已知三角形面积和高,求对应的底a= ;
已知三角形面积和底,求对应的高h= 。
三、当日练兵场——“快”人一刻!
⒌根据已知条件求解:
⒍一个三角形和一个平行四边形:
⑴如果它们等底等高,平行四边形面积是三角形的 。
⑵如果它们的底边相等、面积也相等,平行四边形的高是三角形的 。
⑶如果它们的高相等、面积也相等,平行四边形的底是三角形的 。
⒎判断
⑴三角形的面积是平行四边形面积的一半。 ( )
⑵三角形的面积不可能与平行四边形面积相等,更不可能比它大。 ( )
⑶平行四边形沿对角线剪开,所得的两个三角形完全一样。 ( )
⑷在面积为40m2的平行四边形中画一个三角形,三角形的面积最大只能20m2。 ( )
⑸用长木条钉成一个长方形框,然后把它拉成一个平行四边形,它的周长、面积都发生了变化。 ( )
四、挑战陈景润——“悠”进一步!
⒏下面都是底25m,对应高16m的平行四边形。请计算出各图中三角形面积。
⒐⑴一个平行四边形,如果底不变,高增加3dm,面积就增加24 dm2;如果高不变,底减少2dm,面积就减少24 dm2。平行四边形原来面积是多少?
⑵一个三角形,如果底不变,高增加3dm,面积就增加24 dm2;如果高不变,底减少2dm,面积就减少24 dm2。三角形原来面积是多少?
⒑⑴一个直角三角形,两条直角边长分别是30m和40m,斜边上的高是24m。这个三角形的周长是多少?
⑵将一个正方形从左上角去掉4cm,面积就减少18cm2。现在剩下的梯形面积是多少?
