五年级上册数学导学案-07平行四边形、三角形和梯形练习课苏教版
文档属性
| 名称 | 五年级上册数学导学案-07平行四边形、三角形和梯形练习课苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 104.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 16:23:40 | ||
图片预览

文档简介
五上数学导学案
第二单元:平行四边形、三角形和梯形
教学目标:
1、使学生进一步熟悉平行四边形、三角形和梯形面积的计算公式,熟练地计算不同平行四边形、三角形和梯形的面积。
2、培养灵活利用公式解决实际问题的能力。
3、培养学生良好的合作探究意识。
教学重点:进一步掌握梯形面积的概念,能较熟练掌握平行四边形、三角形和梯形面积的计算方法。
教学难点:能较熟练掌握平行四边形、三角形和梯形面积的计算方法。
一、预习方向标——“仙”人一步!
⒈不规则的图形可以用分一分、移一移、数方格的方法求出它的面积。在数方格时,一般不满一格的都算半格。数方格的方法多用于图形边缘是曲线的图形。
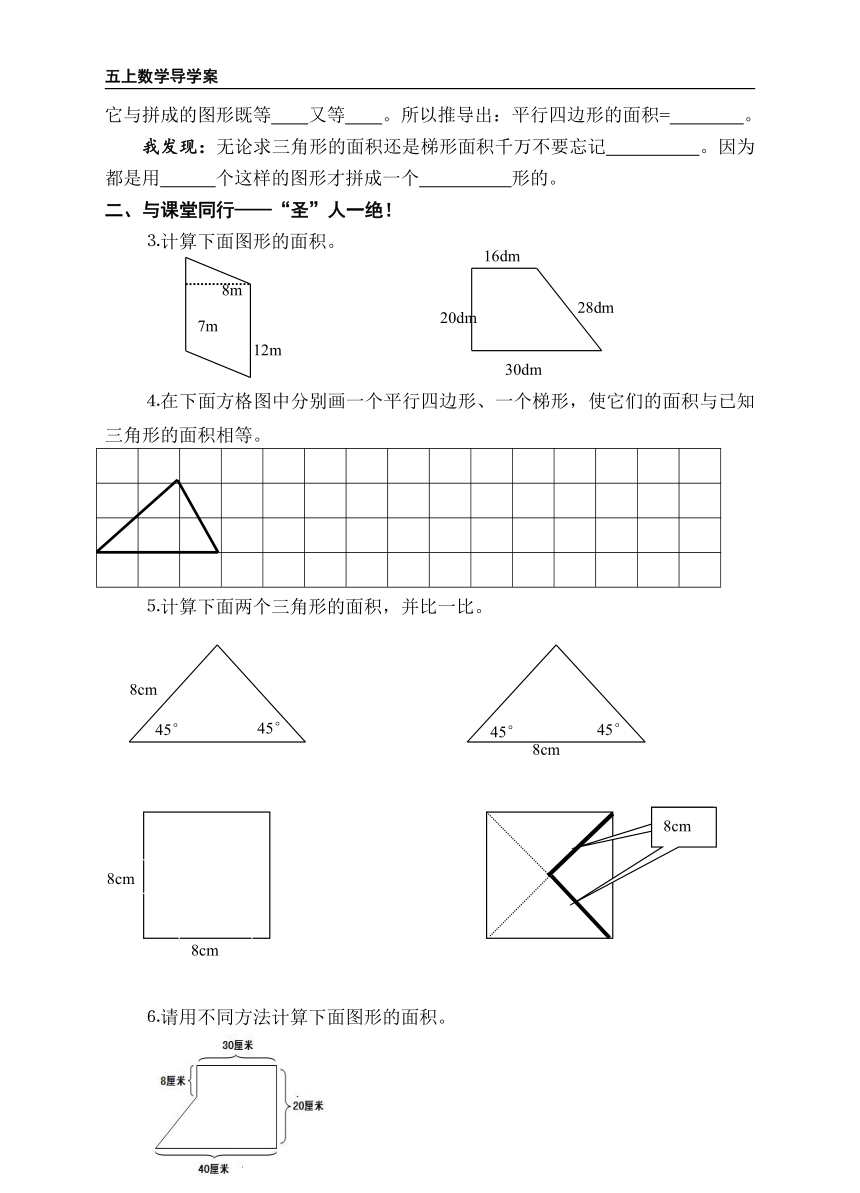
⒉回顾一下面积公式推导过程:
⑴用两个 的三角形可以拼成一个 形。三角形与拼成的图形既等 又等 。所以推导出:三角形的面积= 。
⑵用两个 的梯形也可以拼成一个 形。梯形与拼成的图形, 是相等的,但上底与下底的和才与拼成的平行四边形的 是相等的。所以推导出:梯形的面积= 。
⑶将平行四边形沿着它的一条 剪开,再平移可以拼成一个 形,它与拼成的图形既等 又等 。所以推导出:平行四边形的面积= 。
我发现:无论求三角形的面积还是梯形面积千万不要忘记 。因为都是用 个这样的图形才拼成一个 形的。
二、与课堂同行——“圣”人一绝!
⒊计算下面图形的面积。
⒋在下面方格图中分别画一个平行四边形、一个梯形,使它们的面积与已知三角形的面积相等。
⒌计算下面两个三角形的面积,并比一比。
⒍请用不同方法计算下面图形的面积。
三、当日练兵场——“快”人一刻!
⒎⑴一个梯形上底和下底都扩大3倍,高扩大2倍,面积就扩大6倍。( )
⑵两个面积相等的三角形,他们一定既等底又等高。 ( )
⑶用两根4cm和两根5cm长的小棒可以围成一个面积大于20cm2的平行四边形。 ( )
⒏求下面各图中阴影部分的面积。
四、挑战陈景润——“悠”进一步!
⒐⑴一个梯形,上底3dm,下底5dm,高10dm。面积是多少?
⑵一个梯形,上底3dm,下底5dm,面积是40dm2。高是多少?
⑶一个梯形,上底3dm,高1m,面积是40dm2。下底是多少?
⑷一个梯形,高1m,面积是40dm2。如果上底比下底少2dm,下底是多少?
⒑⑴如下图:阴影部分面积是60cm2,梯形面积是多少平方厘米?
⑵一个直角梯形的上底延长5cm(如图),就成了一个长方形,面积增加了10cm2。如果原来梯形的下底长8cm。那么原来梯形的面积是多少平方厘米?
⑶一个梯形,如果上底延长5cm,就成了一个正方形,面积增加了30cm2。那么原来梯形的面积是多少平方厘米?
⒒⑴如下图,已知EC=3AE,BE=3ED,s△ADE=4cm2,那么梯形的面积是多少?
⑵s△ABC=120dm2,且DC=4BD,AE=3EC, s△ADE=?
⒓万大伯家用78m长的竹篱笆在一块靠墙的空地上围了一个花圃(如下图),这个花圃的面积是多少平方米?
第二单元:平行四边形、三角形和梯形
教学目标:
1、使学生进一步熟悉平行四边形、三角形和梯形面积的计算公式,熟练地计算不同平行四边形、三角形和梯形的面积。
2、培养灵活利用公式解决实际问题的能力。
3、培养学生良好的合作探究意识。
教学重点:进一步掌握梯形面积的概念,能较熟练掌握平行四边形、三角形和梯形面积的计算方法。
教学难点:能较熟练掌握平行四边形、三角形和梯形面积的计算方法。
一、预习方向标——“仙”人一步!
⒈不规则的图形可以用分一分、移一移、数方格的方法求出它的面积。在数方格时,一般不满一格的都算半格。数方格的方法多用于图形边缘是曲线的图形。
⒉回顾一下面积公式推导过程:
⑴用两个 的三角形可以拼成一个 形。三角形与拼成的图形既等 又等 。所以推导出:三角形的面积= 。
⑵用两个 的梯形也可以拼成一个 形。梯形与拼成的图形, 是相等的,但上底与下底的和才与拼成的平行四边形的 是相等的。所以推导出:梯形的面积= 。
⑶将平行四边形沿着它的一条 剪开,再平移可以拼成一个 形,它与拼成的图形既等 又等 。所以推导出:平行四边形的面积= 。
我发现:无论求三角形的面积还是梯形面积千万不要忘记 。因为都是用 个这样的图形才拼成一个 形的。
二、与课堂同行——“圣”人一绝!
⒊计算下面图形的面积。
⒋在下面方格图中分别画一个平行四边形、一个梯形,使它们的面积与已知三角形的面积相等。
⒌计算下面两个三角形的面积,并比一比。
⒍请用不同方法计算下面图形的面积。
三、当日练兵场——“快”人一刻!
⒎⑴一个梯形上底和下底都扩大3倍,高扩大2倍,面积就扩大6倍。( )
⑵两个面积相等的三角形,他们一定既等底又等高。 ( )
⑶用两根4cm和两根5cm长的小棒可以围成一个面积大于20cm2的平行四边形。 ( )
⒏求下面各图中阴影部分的面积。
四、挑战陈景润——“悠”进一步!
⒐⑴一个梯形,上底3dm,下底5dm,高10dm。面积是多少?
⑵一个梯形,上底3dm,下底5dm,面积是40dm2。高是多少?
⑶一个梯形,上底3dm,高1m,面积是40dm2。下底是多少?
⑷一个梯形,高1m,面积是40dm2。如果上底比下底少2dm,下底是多少?
⒑⑴如下图:阴影部分面积是60cm2,梯形面积是多少平方厘米?
⑵一个直角梯形的上底延长5cm(如图),就成了一个长方形,面积增加了10cm2。如果原来梯形的下底长8cm。那么原来梯形的面积是多少平方厘米?
⑶一个梯形,如果上底延长5cm,就成了一个正方形,面积增加了30cm2。那么原来梯形的面积是多少平方厘米?
⒒⑴如下图,已知EC=3AE,BE=3ED,s△ADE=4cm2,那么梯形的面积是多少?
⑵s△ABC=120dm2,且DC=4BD,AE=3EC, s△ADE=?
⒓万大伯家用78m长的竹篱笆在一块靠墙的空地上围了一个花圃(如下图),这个花圃的面积是多少平方米?
