2020沪科版九年级数学上学期第一次月考试卷(word版,含答案)
文档属性
| 名称 | 2020沪科版九年级数学上学期第一次月考试卷(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 146.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 21:27:42 | ||
图片预览



文档简介
沪科版九年级数学第一次月考
(考试时间:90分钟 满分:150分)
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共10小题,每小题4分,共40分).
1.下列函数中,不是反比例函数的是( )
A.x= B.y=-(k≠0)
C.y= D.y=-
2.抛物线y=-x2不具备的性质是( )
A.开口向下 B.对称轴是y轴
C.与y轴不相交 D.最高点是原点
3.将二次函数y=x2-2x+3化为y=(x+h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
4.★反比例函数y=(m+1)xm2-5在各自的象限内,y随x的增大而增大,则m的值是( )
A.2 B.-2 C.±2 D.-
5.(贵港中考)将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线表达式 是( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=2(x-1)2+1 D.y=2(x+1)2+1
6.在平面直角坐标系中,函数y=-x+1与y=-(x-1)2的图象大致是( )
7.已知y=ax2+bx+c的图象如图所示,根据图中提供的信息,可求得使y≥1成立的x的取值范围是( )
A.-1≤x≤3 B.-3≤x≤1
C.x≥-3 D.x≤-1或x≥3
8.(金华中考)如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
A.16米 B.米 C.16米 D.米
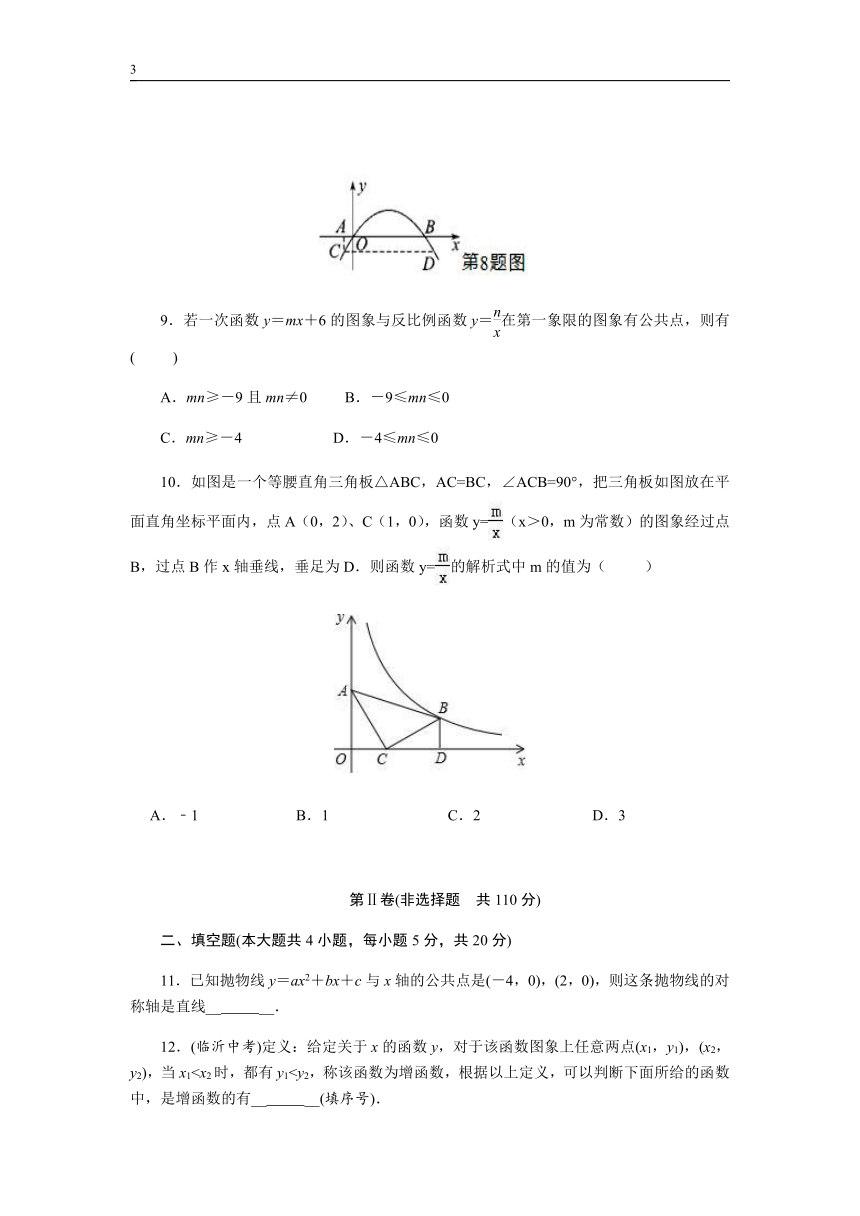
9.若一次函数y=mx+6的图象与反比例函数y=在第一象限的图象有公共点,则有( )
A.mn≥-9且mn≠0 B.-9≤mn≤0
C.mn≥-4 D.-4≤mn≤0
10.如图是一个等腰直角三角板△ABC,AC=BC,∠ACB=90°,把三角板如图放在平面直角坐标平面内,点A(0,2)、C(1,0),函数y=(x>0,m为常数)的图象经过点B,过点B作x轴垂线,垂足为D.则函数y=的解析式中m的值为( )
A.﹣1 B.1 C.2 D.3
第Ⅱ卷(非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线__ __.
12.(临沂中考)定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1①y=2x;②y=-x+1;③y=x2(x>0);④y=-.
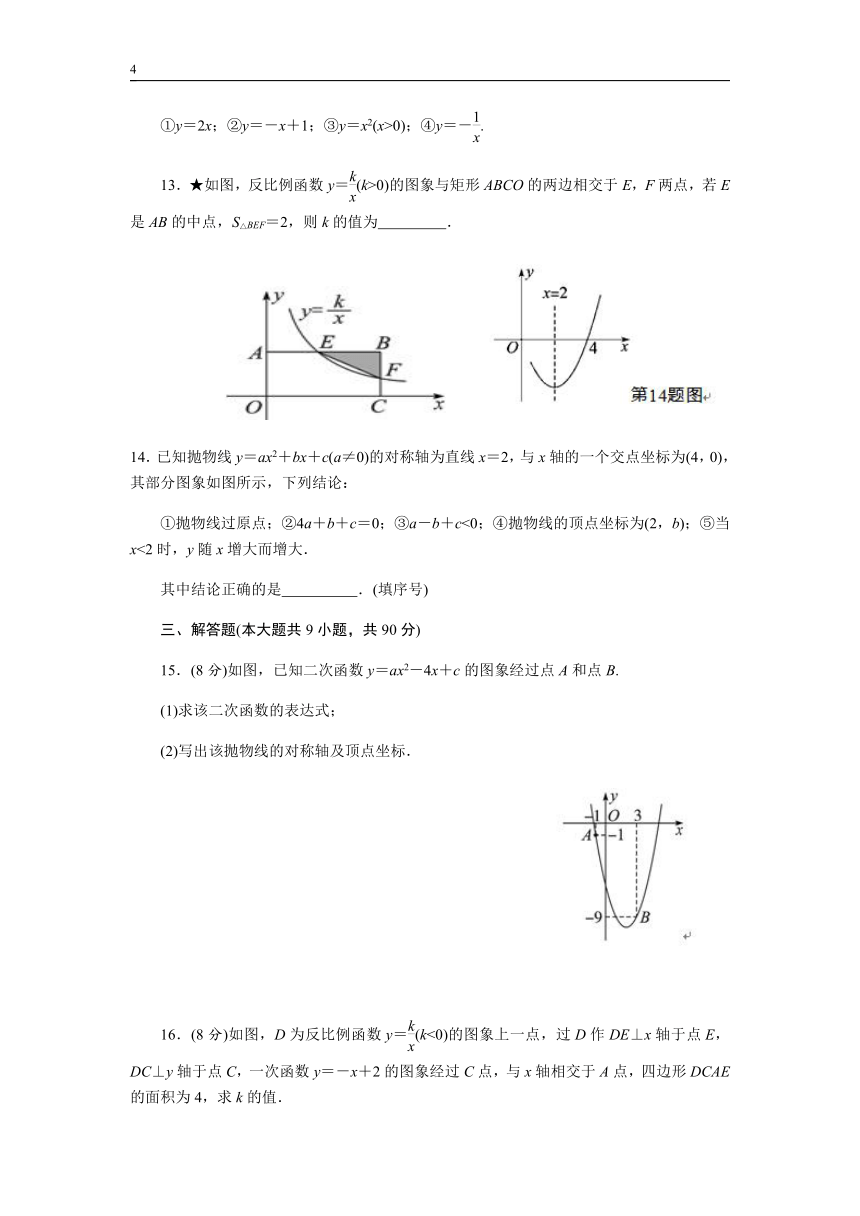
13.★如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .
14.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②4a+b+c=0;③a-b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.
其中结论正确的是 .(填序号)
三、解答题(本大题共9小题,共90分)
15.(8分)如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标.
16.(8分)如图,D为反比例函数y=(k<0)的图象上一点,过D作DE⊥x轴于点E,DC⊥y轴于点C,一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
17.(8分)已知反比例函数y=(k≠0)和一次函数y=x-6.
(1)若一次函数与反比例函数的图象交于点P(2,m),求m和k的值.
(2)当k满足什么条件时,两函数的图象没有交点?
18.(8分)已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的表达式 ;
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
19.(10分)如图,二次函数的图象与x轴相交于A,B两点,与y轴交于点C,点C,D为二次函数图象上的一对对称点,一次函数图象经过B,D两点.
(1)求点D的坐标;
(2)求抛物线与直线的表达式;
(3)指出一次函数值不小于二次函数值的x的取值范围.
20.(10分)(抚顺中考)一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克)
…
50
60
70
80
…
销售量y(千克)
…
100
90
80
70
…
(1)求y与x的函数表达式;
(2)该批发商若想获得4 000元的利润,应将售价定为多少?
(3)该产品每千克售价为多少元时,批发商获得的利润W(元)最大?此时的最大利润为多少元?
21.(12分)(南充中考)反比例函数y=(k≠0)与一次函数y=mx+b(m≠0)交于点 A(1,2k-1).
(1)求反比例函数的表达式;
(2)若一次函数的图象与x轴交于点B,且△AOB的面积为3,求一次函数的表达式.
22.(12分)(丽水中考)丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
23.(14分)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,?0),经过A点的直线交抛物线于点D(2,?3).
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点(a,?0)作直线EF?//?AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
(考试时间:120分钟 满分:150分)
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共10小题,每小题4分,共40分).
1.下列函数中,不是反比例函数的是( D )
A.x= B.y=-(k≠0)
C.y= D.y=-
2.抛物线y=-x2不具备的性质是( C )
A.开口向下 B.对称轴是y轴
C.与y轴不相交 D.最高点是原点
3.将二次函数y=x2-2x+3化为y=(x+h)2+k的形式,结果为( D )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
4.★反比例函数y=(m+1)xm2-5在各自的象限内,y随x的增大而增大,则m的值是( B )
A.2 B.-2 C.±2 D.-
5.(贵港中考)将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线表达式 是( C )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=2(x-1)2+1 D.y=2(x+1)2+1
6.在平面直角坐标系中,函数y=-x+1与y=-(x-1)2的图象大致是( D )
7.已知y=ax2+bx+c的图象如图所示,根据图中提供的信息,可求得使y≥1成立的x的取值范围是( D )
A.-1≤x≤3 B.-3≤x≤1
C.x≥-3 D.x≤-1或x≥3
8.(金华中考)如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( B )
A.16米 B.米 C.16米 D.米
9.若一次函数y=mx+6的图象与反比例函数y=在第一象限的图象有公共点,则有( A )
A.mn≥-9且mn≠0 B.-9≤mn≤0
C.mn≥-4 D.-4≤mn≤0
10.如图是一个等腰直角三角板△ABC,AC=BC,∠ACB=90°,把三角板如图放在平面直角坐标平面内,点A(0,2)、C(1,0),函数y=(x>0,m为常数)的图象经过点B,过点B作x轴垂线,垂足为D.则函数y=的解析式中m的值为( d )
A.﹣1 B.1 C.2 D.3
第Ⅱ卷(非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线__x=-1__.
12.(临沂中考)定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1①y=2x;②y=-x+1;③y=x2(x>0);④y=-.
13.★如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为__8__.
14.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②4a+b+c=0;③a-b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.
其中结论正确的是__①②④__.(填序号)
三、解答题(本大题共9小题,共90分)
15.(8分)如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标.
解:(1)将x=-1,y=-1;x=3,y=-9代入y=ax2-4x+c,解得∴二次函数的表达式为y=x2-4x-6.
(2)由y=x2-4x-6得y=(x-2)2-10,
则对称轴为x=2,顶点坐标为(2,-10).
16.(8分)如图,D为反比例函数y=(k<0)的图象上一点,过D作DE⊥x轴于点E,DC⊥y轴于点C,一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
解:由于一次函数y=-x+2的图象经过C点,与x轴相交于A点,则可求得A(2,0)、C(0,2),即OA=OC=2.
S△AOC=× 2× 2=2,|k|=S矩形DCOE=4-2=2 .又函数图象位于第二象限,k<0,则k=-2.
17.(8分)已知反比例函数y=(k≠0)和一次函数y=x-6.
(1)若一次函数与反比例函数的图象交于点P(2,m),求m和k的值.
(2)当k满足什么条件时,两函数的图象没有交点?
解:(1)m=-4,k=-8;
(2)联立方程得即x2-6x-k=0,无实根,
∴Δ=36+4k<0,∴k<-9,即k<-9时,两函数的图象无交点.
18.(8分)已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的表达式 ;
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
解:(1)y=-x2+2x+8.
(2)当x=0时,y=8,
即抛物钱与y轴的交点D的坐标为(0,8).
过C作CE⊥x轴于E点,
∴S四边形ABCD=S△AOD+S四边形DOEC+S△BCE
=× 2 × 8+×(8+9)× 1+× 3× 9=30.
19.(10分)如图,二次函数的图象与x轴相交于A,B两点,与y轴交于点C,点C,D为二次函数图象上的一对对称点,一次函数图象经过B,D两点.
(1)求点D的坐标;
(2)求抛物线与直线的表达式;
(3)指出一次函数值不小于二次函数值的x的取值范围.
解:(1)由题意知对称轴为直线x=-1,
∴xD+0=-2,∴xD=-2,∴D(-2,3);
(2)y=-x2-2x+3,yBD=-x+1;
(3)当x≤-2或x≥1时,一次函数值不小于二次函数值.
20.(10分)(抚顺中考)一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克)
…
50
60
70
80
…
销售量y(千克)
…
100
90
80
70
…
(1)求y与x的函数表达式;
(2)该批发商若想获得4 000元的利润,应将售价定为多少?
(3)该产品每千克售价为多少元时,批发商获得的利润W(元)最大?此时的最大利润为多少元?
解:(1)设y与x的函数表达式为y=kx+b(k≠0),
根据题意得,解得,
故y与x的函数表达式为y=-x+150;
(2)根据题意得(-x+150)(x-20)=4 000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4 000元的利润,应将售价定为70元/千克;
(3)W与x的函数表达式为W=(-x+150)(x-20)=-x2+170x-3 000=-(x-85)2+4 225,
∵-1<0,∴当x=85时,W值最大,W最大值是4 225,
∴该产品每千克售价为85元时,批发商获得的利润W(元)最大,此时的最大利润为4 225元.
21.(12分)(南充中考)反比例函数y=(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k-1).
(1)求反比例函数的表达式;
(2)若一次函数的图象与x轴交于点B,且△AOB的面积为3,求一次函数的表达式.
解:(1)∵反比例函数y=(k≠0)的图象过点A(1,2k-1),∴=2k-1,解得k=1.∴反比例函数的表达式为y=.
(2)如图,过点A作AM⊥x轴于点M,∵A(1,2k-1),k=1,∴点A(1,1),∴点A到x轴的距离AM=1.
由题意知S△AOB=OB·AM=3,∴OB×1=3,即OB=6.
故B(6,0)或B′(-6,0).
①当一次函数的图象过点A(1,1),B(6,0)时,
解得∴一次函数的表达式为y=-x+.
②当一次函数的图象过点A(1,1),B′(-6,0)时,
解得∴一次函数的表达式为y=x+.
综上可知,一次函数的表达式为y=-x+或y=x+.
22.(12分)(丽水中考)丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
解:(1)根据表中的数据,画图可知图象为反比例函数,设v=,
∵v=75时,t=4,∴k=75×4=300,∴v=.
(2)∵10-7.5=2.5,∴当t=2.5时,v==120>100.
∴汽车上午7:30从丽水出发,不能在上午10:00之前到达杭州市场.
(3)由反比例函数的性质得,当3.5≤t≤4时,75≤v≤.
答:平均速度v的取值范围是75≤v≤.
23.(14分)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,?0),经过A点的直线交抛物线于点D(2,?3).
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点(a,?0)作直线EF?//?AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
23.解:(1)把点B和D的坐标代入抛物线y=-x2+bx+c得:-9+3b+c=0-4+2b+c=3,
解得:b=2,c=3,
∴抛物线的解析式为y=-x2+2x+3;
当y=0时,-x2+2x+3=0,
解得:x=3,或x=-1,
∵B(3,?0),
∴A(-1,?0);
设直线AD的解析式为y=kx+a,
把A和D的坐标代入得:-k+a=02k+a=3,
解得:k=1,a=1,
∴直线AD的解析式为y=x+1;
(2)分两种情况:如图所示:
①当a<-1时,DF?//?AE且DF=AE,
则F点即为(0,?3),
∵AE=-1-a=2,
∴a=-3;
②当a>-1时,显然F应在x轴下方,EF?//?AD且EF=AD,
设F?(a-3,?-3),
由-(a-3)2+2(a-3)+3=-3,
解得:a=4±7;
综上所述,满足条件的a的值为-3或4±7.
(考试时间:90分钟 满分:150分)
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共10小题,每小题4分,共40分).
1.下列函数中,不是反比例函数的是( )
A.x= B.y=-(k≠0)
C.y= D.y=-
2.抛物线y=-x2不具备的性质是( )
A.开口向下 B.对称轴是y轴
C.与y轴不相交 D.最高点是原点
3.将二次函数y=x2-2x+3化为y=(x+h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
4.★反比例函数y=(m+1)xm2-5在各自的象限内,y随x的增大而增大,则m的值是( )
A.2 B.-2 C.±2 D.-
5.(贵港中考)将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线表达式 是( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=2(x-1)2+1 D.y=2(x+1)2+1
6.在平面直角坐标系中,函数y=-x+1与y=-(x-1)2的图象大致是( )
7.已知y=ax2+bx+c的图象如图所示,根据图中提供的信息,可求得使y≥1成立的x的取值范围是( )
A.-1≤x≤3 B.-3≤x≤1
C.x≥-3 D.x≤-1或x≥3
8.(金华中考)如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
A.16米 B.米 C.16米 D.米
9.若一次函数y=mx+6的图象与反比例函数y=在第一象限的图象有公共点,则有( )
A.mn≥-9且mn≠0 B.-9≤mn≤0
C.mn≥-4 D.-4≤mn≤0
10.如图是一个等腰直角三角板△ABC,AC=BC,∠ACB=90°,把三角板如图放在平面直角坐标平面内,点A(0,2)、C(1,0),函数y=(x>0,m为常数)的图象经过点B,过点B作x轴垂线,垂足为D.则函数y=的解析式中m的值为( )
A.﹣1 B.1 C.2 D.3
第Ⅱ卷(非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线__ __.
12.(临沂中考)定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1
13.★如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .
14.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②4a+b+c=0;③a-b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.
其中结论正确的是 .(填序号)
三、解答题(本大题共9小题,共90分)
15.(8分)如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标.
16.(8分)如图,D为反比例函数y=(k<0)的图象上一点,过D作DE⊥x轴于点E,DC⊥y轴于点C,一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
17.(8分)已知反比例函数y=(k≠0)和一次函数y=x-6.
(1)若一次函数与反比例函数的图象交于点P(2,m),求m和k的值.
(2)当k满足什么条件时,两函数的图象没有交点?
18.(8分)已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的表达式 ;
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
19.(10分)如图,二次函数的图象与x轴相交于A,B两点,与y轴交于点C,点C,D为二次函数图象上的一对对称点,一次函数图象经过B,D两点.
(1)求点D的坐标;
(2)求抛物线与直线的表达式;
(3)指出一次函数值不小于二次函数值的x的取值范围.
20.(10分)(抚顺中考)一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克)
…
50
60
70
80
…
销售量y(千克)
…
100
90
80
70
…
(1)求y与x的函数表达式;
(2)该批发商若想获得4 000元的利润,应将售价定为多少?
(3)该产品每千克售价为多少元时,批发商获得的利润W(元)最大?此时的最大利润为多少元?
21.(12分)(南充中考)反比例函数y=(k≠0)与一次函数y=mx+b(m≠0)交于点 A(1,2k-1).
(1)求反比例函数的表达式;
(2)若一次函数的图象与x轴交于点B,且△AOB的面积为3,求一次函数的表达式.
22.(12分)(丽水中考)丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
23.(14分)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,?0),经过A点的直线交抛物线于点D(2,?3).
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点(a,?0)作直线EF?//?AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
(考试时间:120分钟 满分:150分)
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共10小题,每小题4分,共40分).
1.下列函数中,不是反比例函数的是( D )
A.x= B.y=-(k≠0)
C.y= D.y=-
2.抛物线y=-x2不具备的性质是( C )
A.开口向下 B.对称轴是y轴
C.与y轴不相交 D.最高点是原点
3.将二次函数y=x2-2x+3化为y=(x+h)2+k的形式,结果为( D )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
4.★反比例函数y=(m+1)xm2-5在各自的象限内,y随x的增大而增大,则m的值是( B )
A.2 B.-2 C.±2 D.-
5.(贵港中考)将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线表达式 是( C )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=2(x-1)2+1 D.y=2(x+1)2+1
6.在平面直角坐标系中,函数y=-x+1与y=-(x-1)2的图象大致是( D )
7.已知y=ax2+bx+c的图象如图所示,根据图中提供的信息,可求得使y≥1成立的x的取值范围是( D )
A.-1≤x≤3 B.-3≤x≤1
C.x≥-3 D.x≤-1或x≥3
8.(金华中考)如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( B )
A.16米 B.米 C.16米 D.米
9.若一次函数y=mx+6的图象与反比例函数y=在第一象限的图象有公共点,则有( A )
A.mn≥-9且mn≠0 B.-9≤mn≤0
C.mn≥-4 D.-4≤mn≤0
10.如图是一个等腰直角三角板△ABC,AC=BC,∠ACB=90°,把三角板如图放在平面直角坐标平面内,点A(0,2)、C(1,0),函数y=(x>0,m为常数)的图象经过点B,过点B作x轴垂线,垂足为D.则函数y=的解析式中m的值为( d )
A.﹣1 B.1 C.2 D.3
第Ⅱ卷(非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知抛物线y=ax2+bx+c与x轴的公共点是(-4,0),(2,0),则这条抛物线的对称轴是直线__x=-1__.
12.(临沂中考)定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1
13.★如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为__8__.
14.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②4a+b+c=0;③a-b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.
其中结论正确的是__①②④__.(填序号)
三、解答题(本大题共9小题,共90分)
15.(8分)如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标.
解:(1)将x=-1,y=-1;x=3,y=-9代入y=ax2-4x+c,解得∴二次函数的表达式为y=x2-4x-6.
(2)由y=x2-4x-6得y=(x-2)2-10,
则对称轴为x=2,顶点坐标为(2,-10).
16.(8分)如图,D为反比例函数y=(k<0)的图象上一点,过D作DE⊥x轴于点E,DC⊥y轴于点C,一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
解:由于一次函数y=-x+2的图象经过C点,与x轴相交于A点,则可求得A(2,0)、C(0,2),即OA=OC=2.
S△AOC=× 2× 2=2,|k|=S矩形DCOE=4-2=2 .又函数图象位于第二象限,k<0,则k=-2.
17.(8分)已知反比例函数y=(k≠0)和一次函数y=x-6.
(1)若一次函数与反比例函数的图象交于点P(2,m),求m和k的值.
(2)当k满足什么条件时,两函数的图象没有交点?
解:(1)m=-4,k=-8;
(2)联立方程得即x2-6x-k=0,无实根,
∴Δ=36+4k<0,∴k<-9,即k<-9时,两函数的图象无交点.
18.(8分)已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的表达式 ;
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
解:(1)y=-x2+2x+8.
(2)当x=0时,y=8,
即抛物钱与y轴的交点D的坐标为(0,8).
过C作CE⊥x轴于E点,
∴S四边形ABCD=S△AOD+S四边形DOEC+S△BCE
=× 2 × 8+×(8+9)× 1+× 3× 9=30.
19.(10分)如图,二次函数的图象与x轴相交于A,B两点,与y轴交于点C,点C,D为二次函数图象上的一对对称点,一次函数图象经过B,D两点.
(1)求点D的坐标;
(2)求抛物线与直线的表达式;
(3)指出一次函数值不小于二次函数值的x的取值范围.
解:(1)由题意知对称轴为直线x=-1,
∴xD+0=-2,∴xD=-2,∴D(-2,3);
(2)y=-x2-2x+3,yBD=-x+1;
(3)当x≤-2或x≥1时,一次函数值不小于二次函数值.
20.(10分)(抚顺中考)一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克)
…
50
60
70
80
…
销售量y(千克)
…
100
90
80
70
…
(1)求y与x的函数表达式;
(2)该批发商若想获得4 000元的利润,应将售价定为多少?
(3)该产品每千克售价为多少元时,批发商获得的利润W(元)最大?此时的最大利润为多少元?
解:(1)设y与x的函数表达式为y=kx+b(k≠0),
根据题意得,解得,
故y与x的函数表达式为y=-x+150;
(2)根据题意得(-x+150)(x-20)=4 000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4 000元的利润,应将售价定为70元/千克;
(3)W与x的函数表达式为W=(-x+150)(x-20)=-x2+170x-3 000=-(x-85)2+4 225,
∵-1<0,∴当x=85时,W值最大,W最大值是4 225,
∴该产品每千克售价为85元时,批发商获得的利润W(元)最大,此时的最大利润为4 225元.
21.(12分)(南充中考)反比例函数y=(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k-1).
(1)求反比例函数的表达式;
(2)若一次函数的图象与x轴交于点B,且△AOB的面积为3,求一次函数的表达式.
解:(1)∵反比例函数y=(k≠0)的图象过点A(1,2k-1),∴=2k-1,解得k=1.∴反比例函数的表达式为y=.
(2)如图,过点A作AM⊥x轴于点M,∵A(1,2k-1),k=1,∴点A(1,1),∴点A到x轴的距离AM=1.
由题意知S△AOB=OB·AM=3,∴OB×1=3,即OB=6.
故B(6,0)或B′(-6,0).
①当一次函数的图象过点A(1,1),B(6,0)时,
解得∴一次函数的表达式为y=-x+.
②当一次函数的图象过点A(1,1),B′(-6,0)时,
解得∴一次函数的表达式为y=x+.
综上可知,一次函数的表达式为y=-x+或y=x+.
22.(12分)(丽水中考)丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
解:(1)根据表中的数据,画图可知图象为反比例函数,设v=,
∵v=75时,t=4,∴k=75×4=300,∴v=.
(2)∵10-7.5=2.5,∴当t=2.5时,v==120>100.
∴汽车上午7:30从丽水出发,不能在上午10:00之前到达杭州市场.
(3)由反比例函数的性质得,当3.5≤t≤4时,75≤v≤.
答:平均速度v的取值范围是75≤v≤.
23.(14分)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,?0),经过A点的直线交抛物线于点D(2,?3).
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点(a,?0)作直线EF?//?AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
23.解:(1)把点B和D的坐标代入抛物线y=-x2+bx+c得:-9+3b+c=0-4+2b+c=3,
解得:b=2,c=3,
∴抛物线的解析式为y=-x2+2x+3;
当y=0时,-x2+2x+3=0,
解得:x=3,或x=-1,
∵B(3,?0),
∴A(-1,?0);
设直线AD的解析式为y=kx+a,
把A和D的坐标代入得:-k+a=02k+a=3,
解得:k=1,a=1,
∴直线AD的解析式为y=x+1;
(2)分两种情况:如图所示:
①当a<-1时,DF?//?AE且DF=AE,
则F点即为(0,?3),
∵AE=-1-a=2,
∴a=-3;
②当a>-1时,显然F应在x轴下方,EF?//?AD且EF=AD,
设F?(a-3,?-3),
由-(a-3)2+2(a-3)+3=-3,
解得:a=4±7;
综上所述,满足条件的a的值为-3或4±7.
同课章节目录
