沪科版九年级上册 21.2 二次函数图像与性质 同步练习(Word版 含解析)
文档属性
| 名称 | 沪科版九年级上册 21.2 二次函数图像与性质 同步练习(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 609.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览


文档简介
21.2二次函数y=ax2的图象和性质
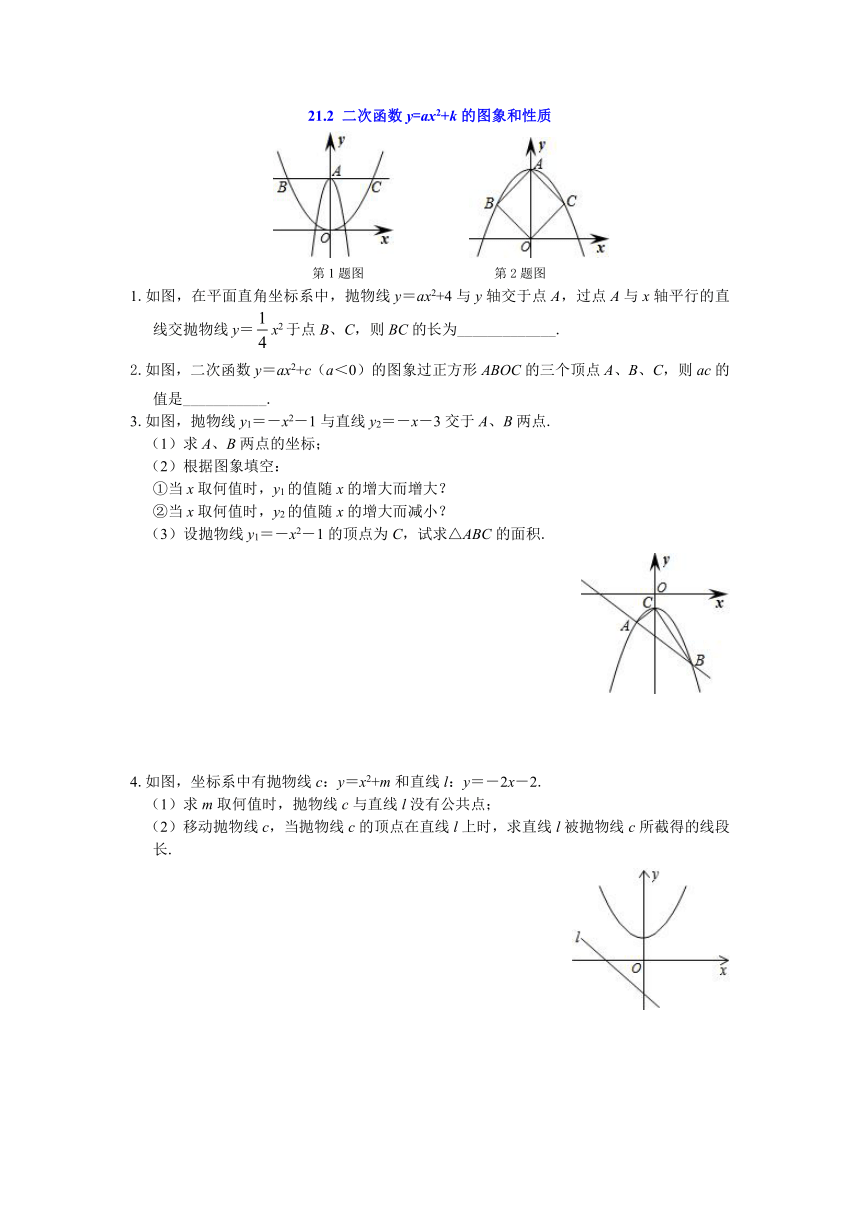
1.如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则=( )
A.2 B. C. D.3
2.如图,已知直线l过A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为4.5,求a的值.
3.如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求△COB的面积.
21.2 二次函数y=ax2+k的图象和性质
第1题图 第2题图
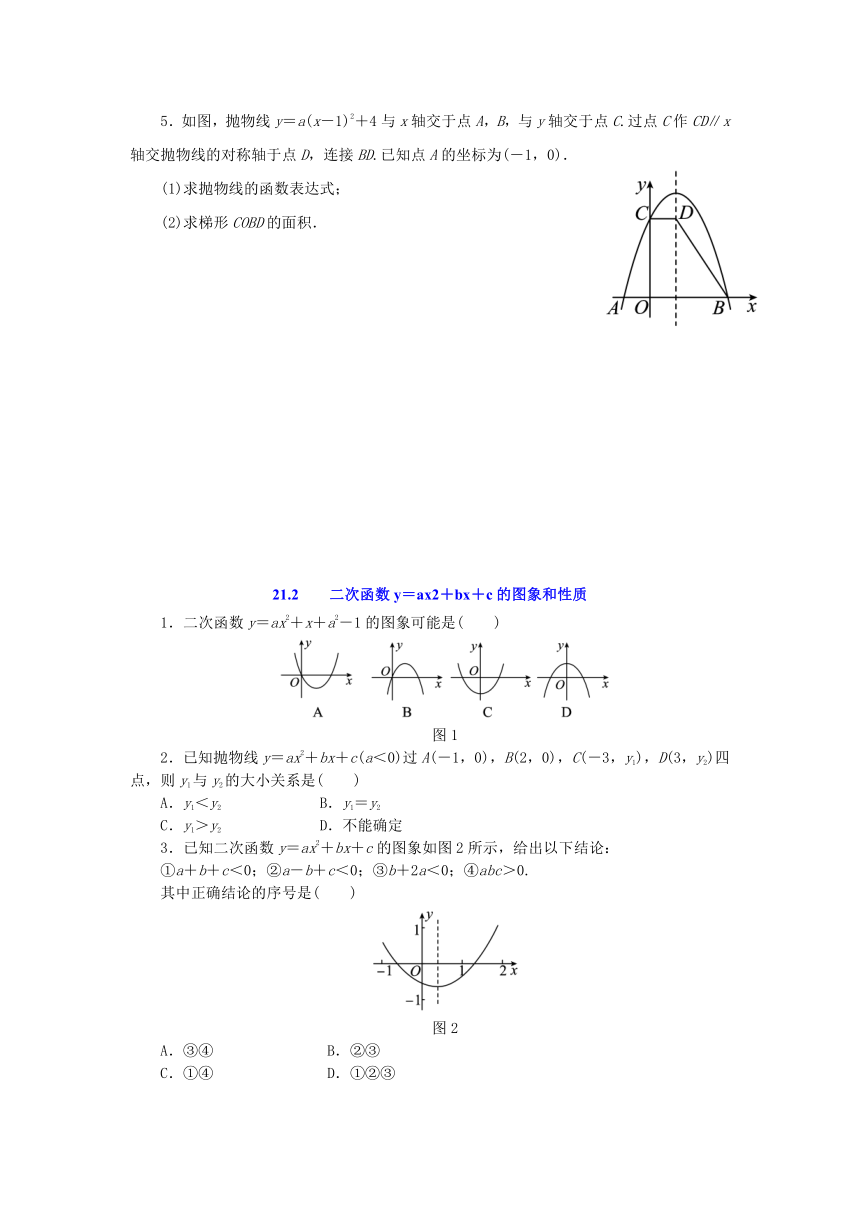
1.如图,在平面直角坐标系中,抛物线y=ax2+4与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B、C,则BC的长为_____________.
2.如图,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是___________.
3.如图,抛物线y1=-x2-1与直线y2=-x-3交于A、B两点.
(1)求A、B两点的坐标;
(2)根据图象填空:
①当x取何值时,y1的值随x的增大而增大?
②当x取何值时,y2的值随x的增大而减小?
(3)设抛物线y1=-x2-1的顶点为C,试求△ABC的面积.
4.如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
(1)求m取何值时,抛物线c与直线l没有公共点;
(2)移动抛物线c,当抛物线c的顶点在直线l上时,求直线l被抛物线c所截得的线段长.
5.如图所示,隧道的截面是由抛物线和矩形构成,矩形的长为8cm,宽为2cm,抛物线可用y=x2+4表示.
(1)一辆货车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货车是否可能通过?
21.2 二次函数y=a(x+h)2+k的图象和性质
1.如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,则下列关系式不正确的是( )
A.k=n B.h=m
C.k<n D.h<0,k<0
2.当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为( )
A.-23≤y≤1 B.-23≤y≤2
C.-7≤y≤1 D.-34≤y≤2
3.如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-2)2-4,其对称轴与两抛物线所围成的阴影部分的面积为( )
A.1 B.2 C.4 D.8
4.在同一平面直角坐标系中,如果两个二次函数y1=a1(x+h1)2+k1与y2=a2(x+h2)2+k2的图象的形状相同,并且对称轴关于y轴对称,那么我们称这两个二次函数互为梦函数.如二次函数y=(x+1)2-1与y=(x-1)2-1互为梦函数,写出二次函数y=2(x+3)2+2的其中一个梦函数为____________.
5.如图,抛物线y=a(x-1)2+4与x轴交于点A,B,与y轴交于点C.过点C作CD∥x轴交抛物线的对称轴于点D,连接BD.已知点A的坐标为(-1,0).
(1)求抛物线的函数表达式;
(2)求梯形COBD的面积.
21.2 二次函数y=ax2+bx+c的图象和性质
1.二次函数y=ax2+x+a2-1的图象可能是( )
图1
2.已知抛物线y=ax2+bx+c(a<0)过A(-1,0),B(2,0),C(-3,y1),D(3,y2)四点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2
C.y1>y2 D.不能确定
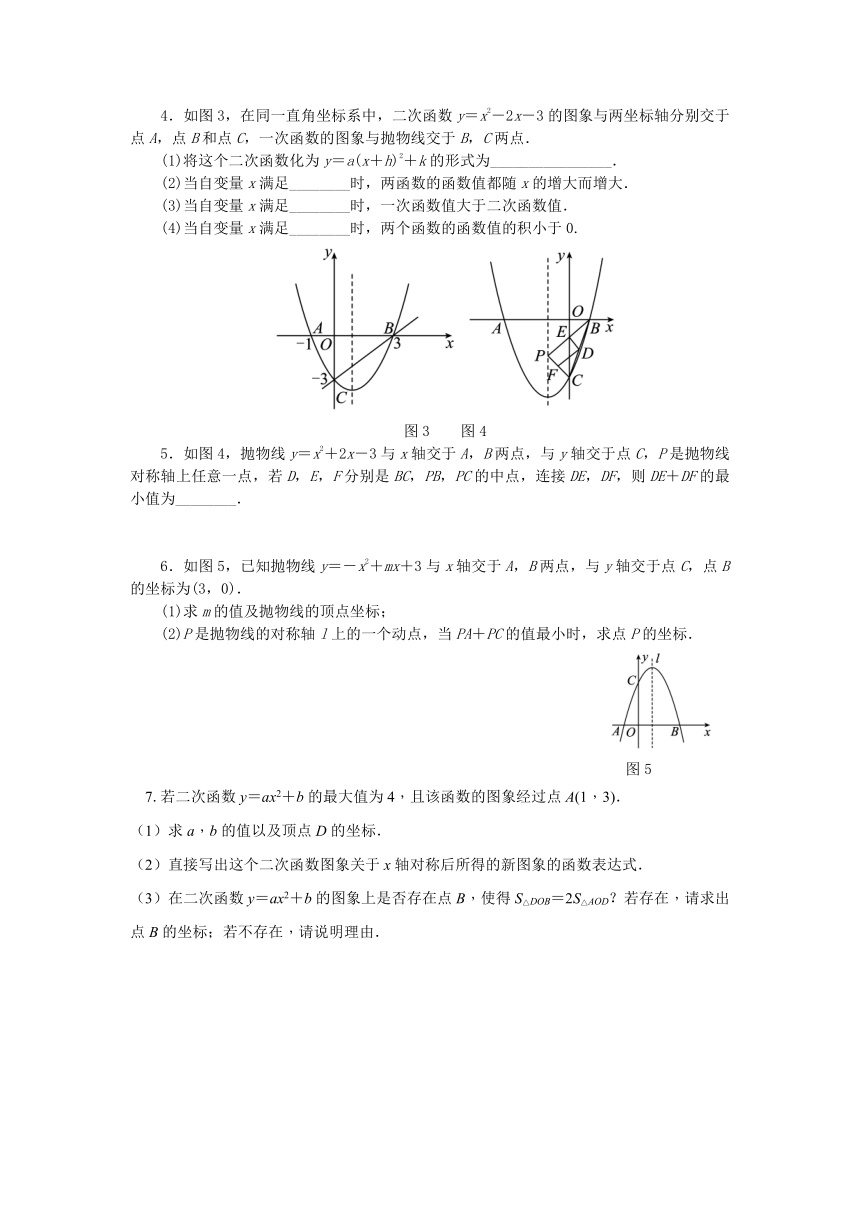
3.已知二次函数y=ax2+bx+c的图象如图2所示,给出以下结论:
①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0.
其中正确结论的序号是( )
图2
A.③④ B.②③
C.①④ D.①②③
4.如图3,在同一直角坐标系中,二次函数y=x2-2x-3的图象与两坐标轴分别交于点A,点B和点C,一次函数的图象与抛物线交于B,C两点.
(1)将这个二次函数化为y=a(x+h)2+k的形式为________________.
(2)当自变量x满足________时,两函数的函数值都随x的增大而增大.
(3)当自变量x满足________时,一次函数值大于二次函数值.
(4)当自变量x满足________时,两个函数的函数值的积小于0.
图3 图4
5.如图4,抛物线y=x2+2x-3与x轴交于A,B两点,与y轴交于点C,P是抛物线对称轴上任意一点,若D,E,F分别是BC,PB,PC的中点,连接DE,DF,则DE+DF的最小值为________.
6.如图5,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0).
(1)求m的值及抛物线的顶点坐标;
(2)P是抛物线的对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
图5
7.若二次函数y=ax2+b的最大值为4,且该函数的图象经过点A(1,3).
(1)求a,b的值以及顶点D的坐标.
(2)直接写出这个二次函数图象关于x轴对称后所得的新图象的函数表达式.
(3)在二次函数y=ax2+b的图象上是否存在点B,使得S△DOB=2S△AOD?若存在,请求出点B的坐标;若不存在,请说明理由.
21.2二次函数y=ax2的图象和性质
1.如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则=( )
A.2 B. C. D.3
解答:设A点坐标为(0,a),(a>0),
则x2=a,解得:x=,
∴B(,a),
当=a时,x=2,
∴C(2,a),
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为2,
∴y1=(2)2=4a,
∴点D的坐标为(2,4a),
∵DE∥AC,
∴点E的纵坐标为4a,
∴=4a,解得:x=4,
∴点E的坐标为(4,4a),
∴DE=4-2=2,
∴==2,
故选:A.
2.如图,已知直线l过A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为4.5,求a的值.
解:设点P的坐标为(x,y),直线AB的解析式为y=kx+b,
将A(4,0),B(0,4)分别代入y=kx+b,
得k=-1,b=4,
故y=-x+4,
∵△AOP的面积为4.5=×4×y,
∴y=,
再把y=代入y=-x+4,得x=,
∴P(,),
把P(,)代入到y=ax2得:a=.
3.如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求△COB的面积.
解:(1)设直线的函数表达式为y=kx+b,
∵A(2,0),B(1,1)都在直线y=kx+b上,
∴,解得:,
∴直线AB的解析式为y=-x+2;
∵点B(1,1)在y=ax2的图象上,
∴a=1,
∴二次函数的解析式为y=x2;
(3)由得:或,
∵点C在第二象限,
∴点C的坐标为(-2,4),
∴S△COB=S△AOC-S△OAB=×2×4-×2×1=3,
即△COB的面积为3.
21.2 二次函数y=ax2+k的图象和性质
1.如图,在平面直角坐标系中,抛物线y=ax2+4与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B、C,则BC的长为_____________.
解答:∵抛物线y=ax2+4与y轴交于点A,
∴A(0,4),
把y=4代入y=x2得:x2=4,
解得:x=±4,
又∵过点A与x轴平行的直线交抛物线y=x2于点B、C,
∴B、C两点的横坐标分别为-4,4,
∴BC==8,
故答案为:8.
2.如图,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是___________.
解答:设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m),
把A、C的坐标代入解析式可得:
c=2m①,am2+c=m②,
把①代入②得:m2a+2m=m,解得:a=-,
则ac=-×2m=-2,
故答案为:-2.
3.如图,抛物线y1=-x2-1与直线y2=-x-3交于A、B两点.
(1)求A、B两点的坐标;
(2)根据图象填空:
①当x取何值时,y1的值随x的增大而增大?
②当x取何值时,y2的值随x的增大而减小?
(3)设抛物线y1=-x2-1的顶点为C,试求△ABC的面积.
解答:(1)由得:,,
∵点A在第三象限,点B在第四象限,
∴A(-1,-2),B(2,-5);
(2)①当x<0时,y1的值随x的增大而增大?
②当x取任何实数时,y2的值随x的增大而减小?
(3)∵抛物线y1=-x2-1的顶点坐标为(0,-1),
∴C(0,-1),
设直线AB与y轴交于点D,则点D的坐标为(0,-3),
∴CD==2,
∴S△ACD=×2×1=1,S△BCD=×2×5=5,
∴S△ABC=S△ACD+ S△BCD=1+5=6,
即△ABC的面积为6.
4.如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
(1)求m取何值时,抛物线c与直线l没有公共点;
(2)移动抛物线c,当抛物线c的顶点在直线l上时,求直线l被抛物线c所截得的线段长.
解答:(1)根据题意得:x2+m=-2x-2,
整理得:x2+2x+m+2=0,
∵抛物线c与直线l没有公共点,
∴△=22-4(m+2)<0,
解得:m>-1,
∴当m>-1时,抛物线c与直线l没有公共点;
(2)∵抛物线c的顶点在直线l上,
∴抛物线c的顶点为(0,-2),
将(0,-2)代入y=x2+m得:m=-2,
∴抛物线c的解析式为y=x2-2,
由得:或,
∴直线l与抛物线c的交点为(0,-2),(-2,2)
∴直线l被抛物线c所截得的线段长为=2.
5.如图所示,隧道的截面是由抛物线和矩形构成,矩形的长为8cm,宽为2cm,抛物线可用y=x2+4表示.
(1)一辆货车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货车是否可能通过?
解答:(1)当货车沿着路面中线行驶时,货车边沿的横坐标为1或-1,
当x=±1时,y=-×(±1)2+4=,
此处隧道高为+2=>4,
故货车能通过隧道.
(2)若隧道内设双行道,此时货车一边靠近隧道中线,另一边沿横坐标为2或-2,
反x=2或-2代入y=x2+4得:y=3,
此处隧道高为3+2=5>4,
故货车能通过隧道.
21.2 二次函数y=a(x+h)2+k的图象和性质
1.[解析]A 根据二次函数表达式确定抛物线的顶点坐标分别为(h,k),(m,n).因为点(h,k)在点(m,n)的下方,所以k=n不正确.故选A.
2.[解析]B ∵a=-1,∴抛物线的开口向下,故有最大值.又∵对称轴为直线x=-3,∴当x=-3时,y有最大值为2;当x=2时,y有最小值为-23,∴当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为-23≤y≤2.
3.[解析]D 如图,由题意可知四边形ABCO为矩形,且点B的坐标为(2,-4),
则S阴影=S矩形ABCO=AB·BC=2×4=8.
4.[答案]y=2(x-3)2+2(答案不唯一)
[解析]梦函数要符合两个条件:①二次项系数的绝对值相同;②对称轴关于y轴对称.
5.解:(1)把A(-1,0)代入y=a(x-1)2+4,得0=4a+4,解得a=-1,
∴抛物线的函数表达式为y=-(x-1)2+4.
(2)令x=0,得y=3,∴OC=3.∵抛物线y=-(x-1)2+4的对称轴是直线x=1,
∴CD=1.又∵A(-1,0),∴B(3,0),∴OB=3,∴S梯形COBD==6.
21.2 二次函数y=ax2+bx+c的图象和性质
1. B.
2. A
3.C
4.[答案]
5.[答案]
6.解:(1)把点B(3,0)代入y=-x2+mx+3,得0=-32+3m+3,解得m=2,
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4).
(2)连接BC交抛物线的对称轴l于点P,则此时PA+PC的值最小.
由题可知C(0,3),由(1)可知,抛物线的对称轴l为直线x=1.
设直线BC的函数表达式为y=kx+b.
则解得
∴直线BC的函数表达式为y=-x+3.
当x=1时,y=-1+3=2,
∴当PA+PC的值最小时,点P的坐标为(1,2).
7.若二次函数y=ax2+b的最大值为4,且该函数的图象经过点A(1,3).
(1)求a,b的值以及顶点D的坐标.
(2)直接写出这个二次函数图象关于x轴对称后所得的新图象的函数表达式.
(3)在二次函数y=ax2+b的图象上是否存在点B,使得S△DOB=2S△AOD?若存在,请求出点B的坐标;若不存在,请说明理由.
解析:(1)由二次函数y=ax2+b的最大值为4可知b=4.
∵函数的图象经过点A(1,3),
∴3=a+4,解得a=-1.
故该二次函数的表达式为y=-x2+4,顶点D的坐标为(0,4).
(2)y=x2-4.
(3)存在.假设存在点B(x,y),使得S△DOB=2S△AOD,
∴OD·|x|=2×OD×1,
解得x=±2.
①当x=2时,则y=-x2+4=0;
②当x=-2时,则y=-x2+4=0.
∴存在满足条件的点B,它的坐标为(2,0)或(-2,0).
1.如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则=( )
A.2 B. C. D.3
2.如图,已知直线l过A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为4.5,求a的值.
3.如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求△COB的面积.
21.2 二次函数y=ax2+k的图象和性质
第1题图 第2题图
1.如图,在平面直角坐标系中,抛物线y=ax2+4与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B、C,则BC的长为_____________.
2.如图,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是___________.
3.如图,抛物线y1=-x2-1与直线y2=-x-3交于A、B两点.
(1)求A、B两点的坐标;
(2)根据图象填空:
①当x取何值时,y1的值随x的增大而增大?
②当x取何值时,y2的值随x的增大而减小?
(3)设抛物线y1=-x2-1的顶点为C,试求△ABC的面积.
4.如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
(1)求m取何值时,抛物线c与直线l没有公共点;
(2)移动抛物线c,当抛物线c的顶点在直线l上时,求直线l被抛物线c所截得的线段长.
5.如图所示,隧道的截面是由抛物线和矩形构成,矩形的长为8cm,宽为2cm,抛物线可用y=x2+4表示.
(1)一辆货车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货车是否可能通过?
21.2 二次函数y=a(x+h)2+k的图象和性质
1.如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,则下列关系式不正确的是( )
A.k=n B.h=m
C.k<n D.h<0,k<0
2.当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为( )
A.-23≤y≤1 B.-23≤y≤2
C.-7≤y≤1 D.-34≤y≤2
3.如图,在平面直角坐标系中,抛物线y1=x2经过平移得到抛物线y2=(x-2)2-4,其对称轴与两抛物线所围成的阴影部分的面积为( )
A.1 B.2 C.4 D.8
4.在同一平面直角坐标系中,如果两个二次函数y1=a1(x+h1)2+k1与y2=a2(x+h2)2+k2的图象的形状相同,并且对称轴关于y轴对称,那么我们称这两个二次函数互为梦函数.如二次函数y=(x+1)2-1与y=(x-1)2-1互为梦函数,写出二次函数y=2(x+3)2+2的其中一个梦函数为____________.
5.如图,抛物线y=a(x-1)2+4与x轴交于点A,B,与y轴交于点C.过点C作CD∥x轴交抛物线的对称轴于点D,连接BD.已知点A的坐标为(-1,0).
(1)求抛物线的函数表达式;
(2)求梯形COBD的面积.
21.2 二次函数y=ax2+bx+c的图象和性质
1.二次函数y=ax2+x+a2-1的图象可能是( )
图1
2.已知抛物线y=ax2+bx+c(a<0)过A(-1,0),B(2,0),C(-3,y1),D(3,y2)四点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2
C.y1>y2 D.不能确定
3.已知二次函数y=ax2+bx+c的图象如图2所示,给出以下结论:
①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0.
其中正确结论的序号是( )
图2
A.③④ B.②③
C.①④ D.①②③
4.如图3,在同一直角坐标系中,二次函数y=x2-2x-3的图象与两坐标轴分别交于点A,点B和点C,一次函数的图象与抛物线交于B,C两点.
(1)将这个二次函数化为y=a(x+h)2+k的形式为________________.
(2)当自变量x满足________时,两函数的函数值都随x的增大而增大.
(3)当自变量x满足________时,一次函数值大于二次函数值.
(4)当自变量x满足________时,两个函数的函数值的积小于0.
图3 图4
5.如图4,抛物线y=x2+2x-3与x轴交于A,B两点,与y轴交于点C,P是抛物线对称轴上任意一点,若D,E,F分别是BC,PB,PC的中点,连接DE,DF,则DE+DF的最小值为________.
6.如图5,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0).
(1)求m的值及抛物线的顶点坐标;
(2)P是抛物线的对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
图5
7.若二次函数y=ax2+b的最大值为4,且该函数的图象经过点A(1,3).
(1)求a,b的值以及顶点D的坐标.
(2)直接写出这个二次函数图象关于x轴对称后所得的新图象的函数表达式.
(3)在二次函数y=ax2+b的图象上是否存在点B,使得S△DOB=2S△AOD?若存在,请求出点B的坐标;若不存在,请说明理由.
21.2二次函数y=ax2的图象和性质
1.如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则=( )
A.2 B. C. D.3
解答:设A点坐标为(0,a),(a>0),
则x2=a,解得:x=,
∴B(,a),
当=a时,x=2,
∴C(2,a),
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为2,
∴y1=(2)2=4a,
∴点D的坐标为(2,4a),
∵DE∥AC,
∴点E的纵坐标为4a,
∴=4a,解得:x=4,
∴点E的坐标为(4,4a),
∴DE=4-2=2,
∴==2,
故选:A.
2.如图,已知直线l过A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为4.5,求a的值.
解:设点P的坐标为(x,y),直线AB的解析式为y=kx+b,
将A(4,0),B(0,4)分别代入y=kx+b,
得k=-1,b=4,
故y=-x+4,
∵△AOP的面积为4.5=×4×y,
∴y=,
再把y=代入y=-x+4,得x=,
∴P(,),
把P(,)代入到y=ax2得:a=.
3.如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求△COB的面积.
解:(1)设直线的函数表达式为y=kx+b,
∵A(2,0),B(1,1)都在直线y=kx+b上,
∴,解得:,
∴直线AB的解析式为y=-x+2;
∵点B(1,1)在y=ax2的图象上,
∴a=1,
∴二次函数的解析式为y=x2;
(3)由得:或,
∵点C在第二象限,
∴点C的坐标为(-2,4),
∴S△COB=S△AOC-S△OAB=×2×4-×2×1=3,
即△COB的面积为3.
21.2 二次函数y=ax2+k的图象和性质
1.如图,在平面直角坐标系中,抛物线y=ax2+4与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B、C,则BC的长为_____________.
解答:∵抛物线y=ax2+4与y轴交于点A,
∴A(0,4),
把y=4代入y=x2得:x2=4,
解得:x=±4,
又∵过点A与x轴平行的直线交抛物线y=x2于点B、C,
∴B、C两点的横坐标分别为-4,4,
∴BC==8,
故答案为:8.
2.如图,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是___________.
解答:设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m),
把A、C的坐标代入解析式可得:
c=2m①,am2+c=m②,
把①代入②得:m2a+2m=m,解得:a=-,
则ac=-×2m=-2,
故答案为:-2.
3.如图,抛物线y1=-x2-1与直线y2=-x-3交于A、B两点.
(1)求A、B两点的坐标;
(2)根据图象填空:
①当x取何值时,y1的值随x的增大而增大?
②当x取何值时,y2的值随x的增大而减小?
(3)设抛物线y1=-x2-1的顶点为C,试求△ABC的面积.
解答:(1)由得:,,
∵点A在第三象限,点B在第四象限,
∴A(-1,-2),B(2,-5);
(2)①当x<0时,y1的值随x的增大而增大?
②当x取任何实数时,y2的值随x的增大而减小?
(3)∵抛物线y1=-x2-1的顶点坐标为(0,-1),
∴C(0,-1),
设直线AB与y轴交于点D,则点D的坐标为(0,-3),
∴CD==2,
∴S△ACD=×2×1=1,S△BCD=×2×5=5,
∴S△ABC=S△ACD+ S△BCD=1+5=6,
即△ABC的面积为6.
4.如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
(1)求m取何值时,抛物线c与直线l没有公共点;
(2)移动抛物线c,当抛物线c的顶点在直线l上时,求直线l被抛物线c所截得的线段长.
解答:(1)根据题意得:x2+m=-2x-2,
整理得:x2+2x+m+2=0,
∵抛物线c与直线l没有公共点,
∴△=22-4(m+2)<0,
解得:m>-1,
∴当m>-1时,抛物线c与直线l没有公共点;
(2)∵抛物线c的顶点在直线l上,
∴抛物线c的顶点为(0,-2),
将(0,-2)代入y=x2+m得:m=-2,
∴抛物线c的解析式为y=x2-2,
由得:或,
∴直线l与抛物线c的交点为(0,-2),(-2,2)
∴直线l被抛物线c所截得的线段长为=2.
5.如图所示,隧道的截面是由抛物线和矩形构成,矩形的长为8cm,宽为2cm,抛物线可用y=x2+4表示.
(1)一辆货车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货车是否可能通过?
解答:(1)当货车沿着路面中线行驶时,货车边沿的横坐标为1或-1,
当x=±1时,y=-×(±1)2+4=,
此处隧道高为+2=>4,
故货车能通过隧道.
(2)若隧道内设双行道,此时货车一边靠近隧道中线,另一边沿横坐标为2或-2,
反x=2或-2代入y=x2+4得:y=3,
此处隧道高为3+2=5>4,
故货车能通过隧道.
21.2 二次函数y=a(x+h)2+k的图象和性质
1.[解析]A 根据二次函数表达式确定抛物线的顶点坐标分别为(h,k),(m,n).因为点(h,k)在点(m,n)的下方,所以k=n不正确.故选A.
2.[解析]B ∵a=-1,∴抛物线的开口向下,故有最大值.又∵对称轴为直线x=-3,∴当x=-3时,y有最大值为2;当x=2时,y有最小值为-23,∴当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为-23≤y≤2.
3.[解析]D 如图,由题意可知四边形ABCO为矩形,且点B的坐标为(2,-4),
则S阴影=S矩形ABCO=AB·BC=2×4=8.
4.[答案]y=2(x-3)2+2(答案不唯一)
[解析]梦函数要符合两个条件:①二次项系数的绝对值相同;②对称轴关于y轴对称.
5.解:(1)把A(-1,0)代入y=a(x-1)2+4,得0=4a+4,解得a=-1,
∴抛物线的函数表达式为y=-(x-1)2+4.
(2)令x=0,得y=3,∴OC=3.∵抛物线y=-(x-1)2+4的对称轴是直线x=1,
∴CD=1.又∵A(-1,0),∴B(3,0),∴OB=3,∴S梯形COBD==6.
21.2 二次函数y=ax2+bx+c的图象和性质
1. B.
2. A
3.C
4.[答案]
5.[答案]
6.解:(1)把点B(3,0)代入y=-x2+mx+3,得0=-32+3m+3,解得m=2,
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4).
(2)连接BC交抛物线的对称轴l于点P,则此时PA+PC的值最小.
由题可知C(0,3),由(1)可知,抛物线的对称轴l为直线x=1.
设直线BC的函数表达式为y=kx+b.
则解得
∴直线BC的函数表达式为y=-x+3.
当x=1时,y=-1+3=2,
∴当PA+PC的值最小时,点P的坐标为(1,2).
7.若二次函数y=ax2+b的最大值为4,且该函数的图象经过点A(1,3).
(1)求a,b的值以及顶点D的坐标.
(2)直接写出这个二次函数图象关于x轴对称后所得的新图象的函数表达式.
(3)在二次函数y=ax2+b的图象上是否存在点B,使得S△DOB=2S△AOD?若存在,请求出点B的坐标;若不存在,请说明理由.
解析:(1)由二次函数y=ax2+b的最大值为4可知b=4.
∵函数的图象经过点A(1,3),
∴3=a+4,解得a=-1.
故该二次函数的表达式为y=-x2+4,顶点D的坐标为(0,4).
(2)y=x2-4.
(3)存在.假设存在点B(x,y),使得S△DOB=2S△AOD,
∴OD·|x|=2×OD×1,
解得x=±2.
①当x=2时,则y=-x2+4=0;
②当x=-2时,则y=-x2+4=0.
∴存在满足条件的点B,它的坐标为(2,0)或(-2,0).
