人教新版 八年级(上)数学 14.2 乘法公式 专项练习(含解析)
文档属性
| 名称 | 人教新版 八年级(上)数学 14.2 乘法公式 专项练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级(上)数学 乘法公式 专项训练
一.选择题(共10小题)
1.下列等式成立的是
A. B.
C. D.
2.下列计算正确的是
A. B.
C. D.
3.下列多项式的乘法可以运用平方差公式计算的是
A. B.
C. D.
4.若,则整式为
A. B. C. D.
5.已知是一个完全平方式,则的值为
A.4 B.4或 C. D.
6.若,,则的值为
A.30 B.39 C.29 D.19
7.若,,且.则
A.1 B.3 C.或3 D.
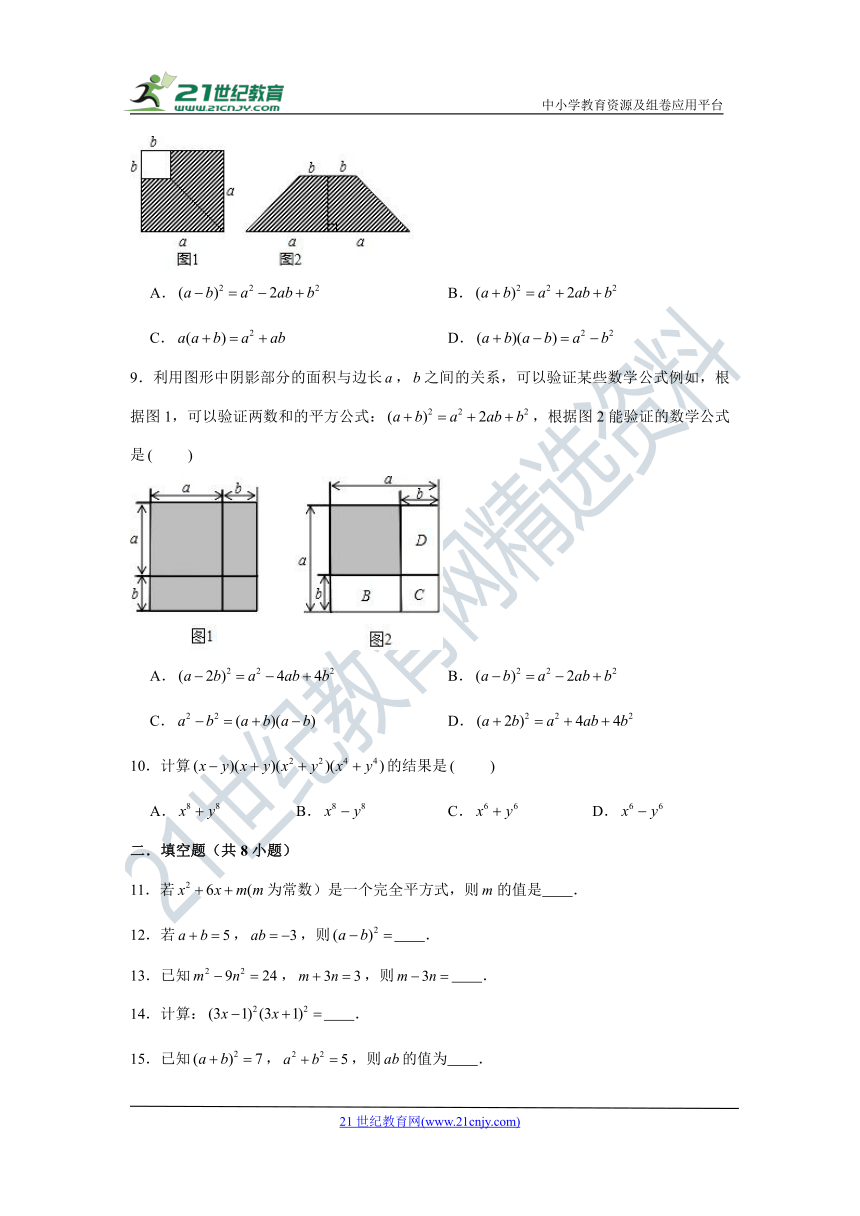
8.如图1,在边长为的正方形中剪去一个边长为的小正方形,把剩下部分沿图1中的虚线剪开后重新拼成一个梯形(如图,利用这两幅图形面积,可以验证的乘法公式是
A. B.
C. D.
9.利用图形中阴影部分的面积与边长,之间的关系,可以验证某些数学公式例如,根据图1,可以验证两数和的平方公式:,根据图2能验证的数学公式是
A. B.
C. D.
10.计算的结果是
A. B. C. D.
二.填空题(共8小题)
11.若为常数)是一个完全平方式,则的值是 .
12.若,,则 .
13.已知,,则 .
14.计算: .
15.已知,,则的值为 .
16.已知整式可以合并,那么代数式的值是 .
17.如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多25平方米,则主卧与客卧的周长差为 .
18.定义※,例如2※.则※的结果为 .
三.解答题(共7小题)
19.计算.
20.计算:
21.计算:
22.已知,,求下列代数式的值:
(1);
(2).
23.某同学化简的解题过程如下
解:原式 (第一步)
(第二步)
(第三步)
(1)该同学的解答过程从第 步开始出现错误.
(2)请写出此题正确的解答过程.
24.【观察探索】用“”“ ”或“”完成以下填空,并观察两边算式,探索规律:
,
,
,
,
【猜想证明】请用一个含字母,的式子表示上以规律,并证明结论的正确性.
【应用拓展】比较代数式与的大小,并说明理由.
25.【知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图1,是用长为,宽为的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分(小正方形)的面积,可以得到、、三者之间的等量关系式: ;
【知识迁移】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式: ;
【成果运用】利用上面所得的结论解答:
(1)已知,,求的值;
(2)已知,求的值.
参考答案
一.选择题(共10小题)
1.下列等式成立的是
A. B.
C. D.
解:.,故本选项不合题意;
.,正确;
.,故本选项不合题意;
.,故本选项不合题意.
故选:.
2.下列计算正确的是
A. B.
C. D.
解:、,故本选项不符合题意;
、,故本选项不符合题意;
、,故本选项不符合题意;
、,故本选项符合题意;
故选:.
3.下列多项式的乘法可以运用平方差公式计算的是
A. B.
C. D.
解:能利用平方差公式计算的多项式的特点是:两个两项式相乘,有一项相同,另一项互为相反数.
、不能用平方差公式进行计算,故本选项不符合题意;
、能用平方差公式进行计算,故本选项符合题意;
、不能用平方差公式进行计算,故本选项不符合题意;
、不能用平方差公式进行计算,故本选项不符合题意.
故选:.
4.若,则整式为
A. B. C. D.
解:因为,,
所以,
故选:.
5.已知是一个完全平方式,则的值为
A.4 B.4或 C. D.
解:是一个完全平方式,
,
解得:或,
故选:.
6.若,,则的值为
A.30 B.39 C.29 D.19
解:,,
原式,
故选:.
7.若,,且.则
A.1 B.3 C.或3 D.
解:.则
,
,,
,
,
,
故选:.
8.如图1,在边长为的正方形中剪去一个边长为的小正方形,把剩下部分沿图1中的虚线剪开后重新拼成一个梯形(如图,利用这两幅图形面积,可以验证的乘法公式是
A. B.
C. D.
解:图1阴影部分的面积等于,
图2梯形的面积是
根据两者阴影部分面积相等,可知
比较各选项,只有符合题意
故选:.
9.利用图形中阴影部分的面积与边长,之间的关系,可以验证某些数学公式例如,根据图1,可以验证两数和的平方公式:,根据图2能验证的数学公式是
A. B.
C. D.
解:图2阴影部分的面积为,大正方形的面积为,矩形的面积为,矩形的面积为,正方形的面积为,
因此有,,
故选:.
10.计算的结果是
A. B. C. D.
解:
,
故选:.
二.填空题(共8小题)
11.若为常数)是一个完全平方式,则的值是 9 .
解:为常数)是一个完全平方式,
,
故答案为:9.
12.若,,则 37 .
解:原式,
,,
原式.
故答案是:37.
13.已知,,则 8 .
解:因为,,,
所以,
所以,
故答案为:8.
14.计算: .
解:
.
故答案为:.
15.已知,,则的值为 1 .
解:,
,
,
,
.
故答案为1.
16.已知整式可以合并,那么代数式的值是 6 .
解:整式可以合并,
,,
,
故答案为:6.
17.如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多25平方米,则主卧与客卧的周长差为 20米 .
解:设客卧的边长为米,主卧的边长为米,
房屋的边长为米,
客卧的面积为平方米,主卧的面积为平方米,房屋的总面积为平方米,
客卧与主卧的面积和为平方米,
阴影部分的面积为平方米,
主卧与客卧面积之和比阴影部多25平方米,
,
,
,
,
主卧的周长与客卧的周长差为米,
故答案为20米.
18.定义※,例如2※.则※的结果为 .
解:根据题意得:
※.
故答案为:.
三.解答题(共7小题)
19.计算.
解:原式
.
20.计算:
解:原式
.
21.计算:
解:原式
.
22.已知,,求下列代数式的值:
(1);
(2).
解:(1),
,
,
,
;
(2),,
,
或,
,
当时,;
当时,.
23.某同学化简的解题过程如下
解:原式 (第一步)
(第二步)
(第三步)
(1)该同学的解答过程从第 一 步开始出现错误.
(2)请写出此题正确的解答过程.
解:(1)该同学从第一步开始出现错误;
故答案为:一
(2)原式
24.【观察探索】用“”“ ”或“”完成以下填空,并观察两边算式,探索规律:
,
,
,
,
【猜想证明】请用一个含字母,的式子表示上以规律,并证明结论的正确性.
【应用拓展】比较代数式与的大小,并说明理由.
解:【观察探索】
,
,
故答案为:,;
【猜想证明】
规律:;
证明:因为,
所以;
【应用拓展】
解:,
,
根据“猜想证明”的结论,得:,
所以,,
即.
25.【知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图1,是用长为,宽为的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分(小正方形)的面积,可以得到、、三者之间的等量关系式: ;
【知识迁移】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式: ;
【成果运用】利用上面所得的结论解答:
(1)已知,,求的值;
(2)已知,求的值.
解:【知识生成】
如图1,方法一:已知边长直接求面积为;
方法二:阴影面积是大正方形面积减去四个长方形面积,
面积为,
由阴影部分面积相等可得;
故答案为:;
【知识迁移】
方法一:正方体棱长为,
体积为,
方法二:正方体体积是长方体和小正方体的体积和,即,
;
故答案为:;
(1)由,
可得,
,,
,
,
;
(2),
,,
;
.
_21?????????è?????(www.21cnjy.com)_
八年级(上)数学 乘法公式 专项训练
一.选择题(共10小题)
1.下列等式成立的是
A. B.
C. D.
2.下列计算正确的是
A. B.
C. D.
3.下列多项式的乘法可以运用平方差公式计算的是
A. B.
C. D.
4.若,则整式为
A. B. C. D.
5.已知是一个完全平方式,则的值为
A.4 B.4或 C. D.
6.若,,则的值为
A.30 B.39 C.29 D.19
7.若,,且.则
A.1 B.3 C.或3 D.
8.如图1,在边长为的正方形中剪去一个边长为的小正方形,把剩下部分沿图1中的虚线剪开后重新拼成一个梯形(如图,利用这两幅图形面积,可以验证的乘法公式是
A. B.
C. D.
9.利用图形中阴影部分的面积与边长,之间的关系,可以验证某些数学公式例如,根据图1,可以验证两数和的平方公式:,根据图2能验证的数学公式是
A. B.
C. D.
10.计算的结果是
A. B. C. D.
二.填空题(共8小题)
11.若为常数)是一个完全平方式,则的值是 .
12.若,,则 .
13.已知,,则 .
14.计算: .
15.已知,,则的值为 .
16.已知整式可以合并,那么代数式的值是 .
17.如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多25平方米,则主卧与客卧的周长差为 .
18.定义※,例如2※.则※的结果为 .
三.解答题(共7小题)
19.计算.
20.计算:
21.计算:
22.已知,,求下列代数式的值:
(1);
(2).
23.某同学化简的解题过程如下
解:原式 (第一步)
(第二步)
(第三步)
(1)该同学的解答过程从第 步开始出现错误.
(2)请写出此题正确的解答过程.
24.【观察探索】用“”“ ”或“”完成以下填空,并观察两边算式,探索规律:
,
,
,
,
【猜想证明】请用一个含字母,的式子表示上以规律,并证明结论的正确性.
【应用拓展】比较代数式与的大小,并说明理由.
25.【知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图1,是用长为,宽为的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分(小正方形)的面积,可以得到、、三者之间的等量关系式: ;
【知识迁移】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式: ;
【成果运用】利用上面所得的结论解答:
(1)已知,,求的值;
(2)已知,求的值.
参考答案
一.选择题(共10小题)
1.下列等式成立的是
A. B.
C. D.
解:.,故本选项不合题意;
.,正确;
.,故本选项不合题意;
.,故本选项不合题意.
故选:.
2.下列计算正确的是
A. B.
C. D.
解:、,故本选项不符合题意;
、,故本选项不符合题意;
、,故本选项不符合题意;
、,故本选项符合题意;
故选:.
3.下列多项式的乘法可以运用平方差公式计算的是
A. B.
C. D.
解:能利用平方差公式计算的多项式的特点是:两个两项式相乘,有一项相同,另一项互为相反数.
、不能用平方差公式进行计算,故本选项不符合题意;
、能用平方差公式进行计算,故本选项符合题意;
、不能用平方差公式进行计算,故本选项不符合题意;
、不能用平方差公式进行计算,故本选项不符合题意.
故选:.
4.若,则整式为
A. B. C. D.
解:因为,,
所以,
故选:.
5.已知是一个完全平方式,则的值为
A.4 B.4或 C. D.
解:是一个完全平方式,
,
解得:或,
故选:.
6.若,,则的值为
A.30 B.39 C.29 D.19
解:,,
原式,
故选:.
7.若,,且.则
A.1 B.3 C.或3 D.
解:.则
,
,,
,
,
,
故选:.
8.如图1,在边长为的正方形中剪去一个边长为的小正方形,把剩下部分沿图1中的虚线剪开后重新拼成一个梯形(如图,利用这两幅图形面积,可以验证的乘法公式是
A. B.
C. D.
解:图1阴影部分的面积等于,
图2梯形的面积是
根据两者阴影部分面积相等,可知
比较各选项,只有符合题意
故选:.
9.利用图形中阴影部分的面积与边长,之间的关系,可以验证某些数学公式例如,根据图1,可以验证两数和的平方公式:,根据图2能验证的数学公式是
A. B.
C. D.
解:图2阴影部分的面积为,大正方形的面积为,矩形的面积为,矩形的面积为,正方形的面积为,
因此有,,
故选:.
10.计算的结果是
A. B. C. D.
解:
,
故选:.
二.填空题(共8小题)
11.若为常数)是一个完全平方式,则的值是 9 .
解:为常数)是一个完全平方式,
,
故答案为:9.
12.若,,则 37 .
解:原式,
,,
原式.
故答案是:37.
13.已知,,则 8 .
解:因为,,,
所以,
所以,
故答案为:8.
14.计算: .
解:
.
故答案为:.
15.已知,,则的值为 1 .
解:,
,
,
,
.
故答案为1.
16.已知整式可以合并,那么代数式的值是 6 .
解:整式可以合并,
,,
,
故答案为:6.
17.如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多25平方米,则主卧与客卧的周长差为 20米 .
解:设客卧的边长为米,主卧的边长为米,
房屋的边长为米,
客卧的面积为平方米,主卧的面积为平方米,房屋的总面积为平方米,
客卧与主卧的面积和为平方米,
阴影部分的面积为平方米,
主卧与客卧面积之和比阴影部多25平方米,
,
,
,
,
主卧的周长与客卧的周长差为米,
故答案为20米.
18.定义※,例如2※.则※的结果为 .
解:根据题意得:
※.
故答案为:.
三.解答题(共7小题)
19.计算.
解:原式
.
20.计算:
解:原式
.
21.计算:
解:原式
.
22.已知,,求下列代数式的值:
(1);
(2).
解:(1),
,
,
,
;
(2),,
,
或,
,
当时,;
当时,.
23.某同学化简的解题过程如下
解:原式 (第一步)
(第二步)
(第三步)
(1)该同学的解答过程从第 一 步开始出现错误.
(2)请写出此题正确的解答过程.
解:(1)该同学从第一步开始出现错误;
故答案为:一
(2)原式
24.【观察探索】用“”“ ”或“”完成以下填空,并观察两边算式,探索规律:
,
,
,
,
【猜想证明】请用一个含字母,的式子表示上以规律,并证明结论的正确性.
【应用拓展】比较代数式与的大小,并说明理由.
解:【观察探索】
,
,
故答案为:,;
【猜想证明】
规律:;
证明:因为,
所以;
【应用拓展】
解:,
,
根据“猜想证明”的结论,得:,
所以,,
即.
25.【知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图1,是用长为,宽为的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分(小正方形)的面积,可以得到、、三者之间的等量关系式: ;
【知识迁移】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式: ;
【成果运用】利用上面所得的结论解答:
(1)已知,,求的值;
(2)已知,求的值.
解:【知识生成】
如图1,方法一:已知边长直接求面积为;
方法二:阴影面积是大正方形面积减去四个长方形面积,
面积为,
由阴影部分面积相等可得;
故答案为:;
【知识迁移】
方法一:正方体棱长为,
体积为,
方法二:正方体体积是长方体和小正方体的体积和,即,
;
故答案为:;
(1)由,
可得,
,,
,
,
;
(2),
,,
;
.
_21?????????è?????(www.21cnjy.com)_
