人教新版 八年级(上)数学 14.2乘法公式 专项训练(含解析)
文档属性
| 名称 | 人教新版 八年级(上)数学 14.2乘法公式 专项训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 16:17:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级(上)数学 乘法公式 专项训练
一.选择题(共10小题)
1.下列式子中,能用平方差公式运算的是
A. B. C. D.
2.计算的结果是
A. B. C. D.
3.为了运用平方差公式计算,下列变形正确的是
A. B.
C. D.
4.若,,求的值是
A.4 B. C.2 D.
5.关于的二次三项式是一个完全平方式,则的值应为
A. B. C. D.
6.若,,则的值是
A.11 B.21 C.29 D.49
7.若,,则
A. B.3 C. D.4
8.为了美化城市,经统一规划,将一块正方形草坪的南北方向增加,东西方向减少,则改造后得到长方形草坪与原正方形草坪面积相比,结果是
A.保持不变 B.增加了 C.增加了 D.减少了
9.数形结合是初中数学重要的思想方法,下图就是用几何图形描述了一个重要的数学公式,这个公式是
A. B.
C. D.
10.如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪拼成一个矩形,通过计算两个图形阴影部分的面积,验证了一个等式,则这个等式是
A. B.
C. D.
二.填空题(共9小题)
11.计算: .
12.若,,则的值为 .
13.若是一个完全平方式,则 .
14.若,,则的值是 .
15.若,则的值是 .
16.已知,,则的值为 .
17.如果多项式加上一个单项式后能成为一个完全平方式,那么加上的这个单项式是 .(填一个即可).
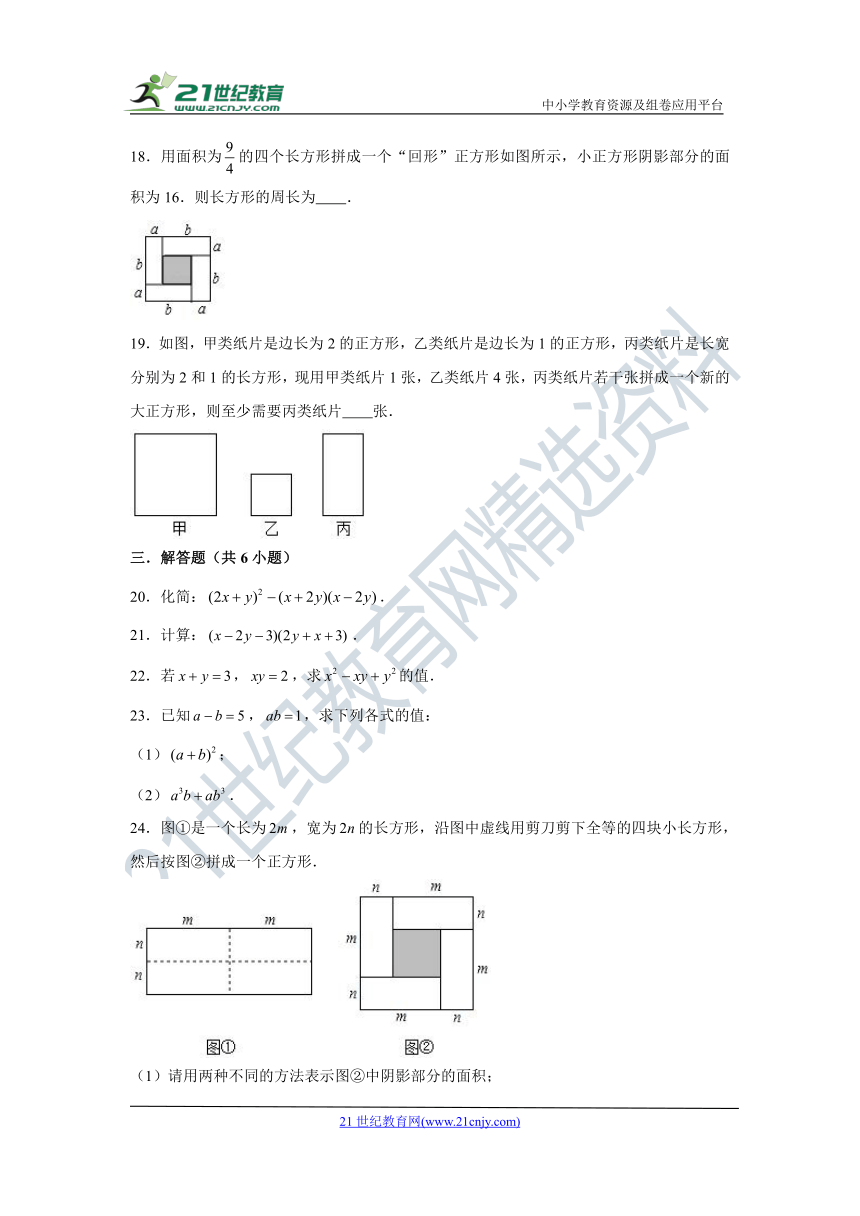
18.用面积为的四个长方形拼成一个“回形”正方形如图所示,小正方形阴影部分的面积为16.则长方形的周长为 .
19.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长宽分别为2和1的长方形,现用甲类纸片1张,乙类纸片4张,丙类纸片若干张拼成一个新的大正方形,则至少需要丙类纸片 张.
三.解答题(共6小题)
20.化简:.
21.计算:.
22.若,,求的值.
23.已知,,求下列各式的值:
(1);
(2).
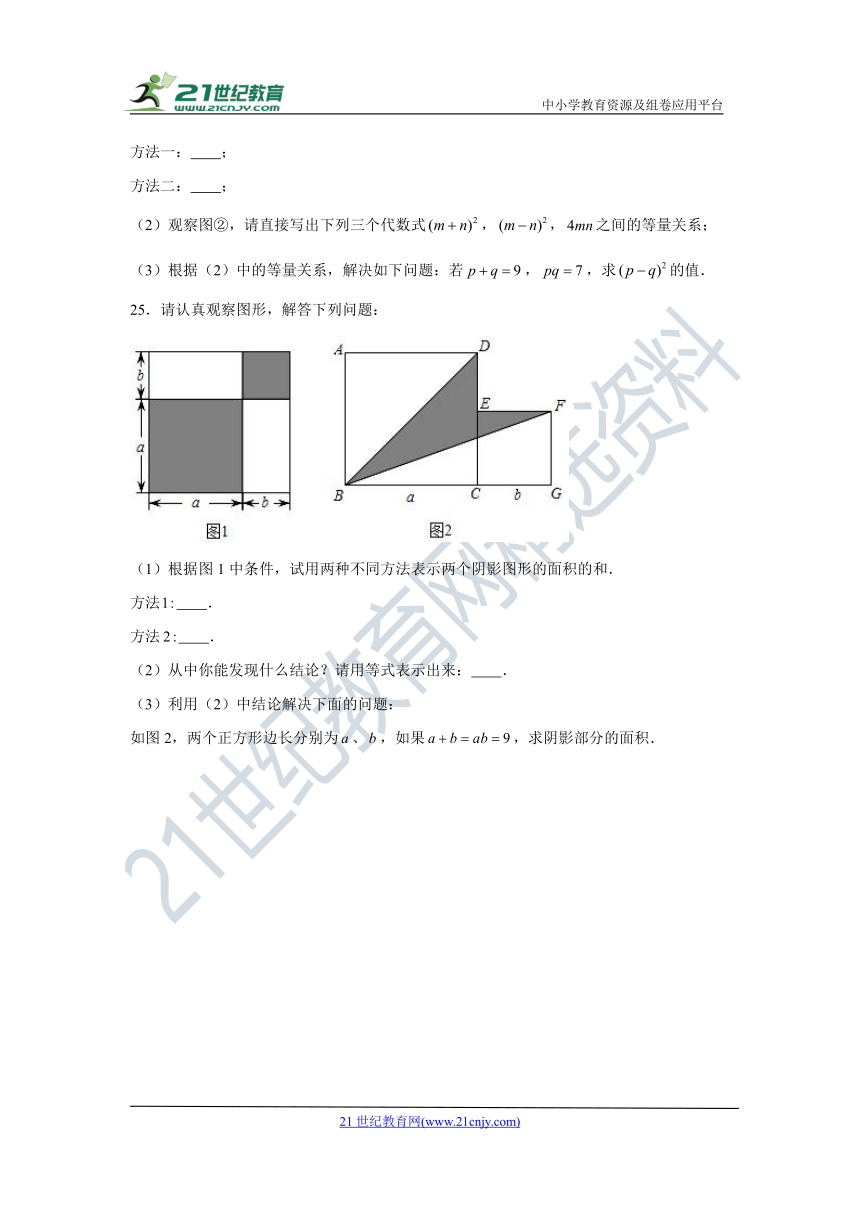
24.图①是一个长为,宽为的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积;
方法一: ;
方法二: ;
(2)观察图②,请直接写出下列三个代数式,,之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若,,求的值.
25.请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法 .
方法 .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为、,如果,求阴影部分的面积.
参考答案
一.选择题(共10小题)
1.下列式子中,能用平方差公式运算的是
A. B. C. D.
解:、中存在相同项,没有相反项,不能用平方差公式计算,故本选项不符合题意;
、两项都是相同,不能用平方差公式计算,故本选项不符合题意;
、存在相同的项与互为相反数的项,能用平方差公式计算,故本选项符合题意;
、中两项都是相反项,没有相同项,不能用平方差公式计算,故本选项不符合题意;
故选:.
2.计算的结果是
A. B. C. D.
解:原式
.
故选:.
3.为了运用平方差公式计算,下列变形正确的是
A. B.
C. D.
解:运用平方差公式计算,
应变形为,
故选:.
4.若,,求的值是
A.4 B. C.2 D.
解:,,
,
,
,
,
故选:.
5.关于的二次三项式是一个完全平方式,则的值应为
A. B. C. D.
解:是完全平方式,
,
.
故选:.
6.若,,则的值是
A.11 B.21 C.29 D.49
解:因为,,
所以;
故选:.
7.若,,则
A. B.3 C. D.4
解:,,
,
,
,
.
故选:.
8.为了美化城市,经统一规划,将一块正方形草坪的南北方向增加,东西方向减少,则改造后得到长方形草坪与原正方形草坪面积相比,结果是
A.保持不变 B.增加了 C.增加了 D.减少了
解:设正方形草坪的原边长为,则面积为;
将一正方形草坪的南北方向增加,东西方向缩短后,边长为,,
面积为.
故减少.
故选:.
9.数形结合是初中数学重要的思想方法,下图就是用几何图形描述了一个重要的数学公式,这个公式是
A. B.
C. D.
解:图1中阴影部分面积等于大正方形的面积,减去小正方形的面积,即;
图2中阴影部分为长等于,宽等于的长方形,其面积等于,
二者面积相等,则有.
比较各选项,可知只有符合题意.
故选:.
10.如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪拼成一个矩形,通过计算两个图形阴影部分的面积,验证了一个等式,则这个等式是
A. B.
C. D.
解:左图的阴影部分的面积为,右图的阴影部分的面积为,
因此有为,
故选:.
二.填空题(共9小题)
11.计算: .
解:.
故答案为:.
12.若,,则的值为 2 .
解:,,
.
故答案为:2.
13.若是一个完全平方式,则 12或 .
解:是一个完全平方式,
,
解得:或,
故答案为:12或.
14.若,,则的值是 2020 .
解:,,
.
故答案为2020.
15.若,则的值是 25 .
解:,
原式.
故答案为:25.
16.已知,,则的值为 25 .
解:,,
.
.
故答案是:25.
17.如果多项式加上一个单项式后能成为一个完全平方式,那么加上的这个单项式是 .(填一个即可).
解:,
即加上的这个单项式是,
故答案为:.
18.用面积为的四个长方形拼成一个“回形”正方形如图所示,小正方形阴影部分的面积为16.则长方形的周长为 10 .
解:由题意可得,,
,
,(舍去)
长方形的周长,
故答案为10.
19.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长宽分别为2和1的长方形,现用甲类纸片1张,乙类纸片4张,丙类纸片若干张拼成一个新的大正方形,则至少需要丙类纸片 4 张.
解:甲类纸片1张,乙类纸片4张,总面积是,大于8的完全平方数依次是9,16,,而丙的面积是2,因而不可能是9;
当总面积是16时,取的丙纸片的总面积是8,因而是4张.
因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.
故答案为:4.
三.解答题(共6小题)
20.化简:.
解:原式
.
21.计算:.
解:
.
22.若,,求的值.
解:把两边平方得:,即,
将代入得:,即,
则原式.
23.已知,,求下列各式的值:
(1);
(2).
解:(1)原式
;
(2)原式
.
24.图①是一个长为,宽为的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积;
方法一: ;
方法二: ;
(2)观察图②,请直接写出下列三个代数式,,之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若,,求的值.
解:(1)方法一:,
方法二:,
故答案为:;;
(2);
(3)当,时,.
25.请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法 .
方法 .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为、,如果,求阴影部分的面积.
解:(1)图1,两个阴影正方形的面积和:,
大正方形的面积减去两个长方形的面积:,
故答案为:,;
(2)两个数的平方和等于这两个数和的平方减去这两个数积的2倍,即:;
故答案为:;
(3)如图2,阴影部分的面积为:
.
_21?????????è?????(www.21cnjy.com)_
八年级(上)数学 乘法公式 专项训练
一.选择题(共10小题)
1.下列式子中,能用平方差公式运算的是
A. B. C. D.
2.计算的结果是
A. B. C. D.
3.为了运用平方差公式计算,下列变形正确的是
A. B.
C. D.
4.若,,求的值是
A.4 B. C.2 D.
5.关于的二次三项式是一个完全平方式,则的值应为
A. B. C. D.
6.若,,则的值是
A.11 B.21 C.29 D.49
7.若,,则
A. B.3 C. D.4
8.为了美化城市,经统一规划,将一块正方形草坪的南北方向增加,东西方向减少,则改造后得到长方形草坪与原正方形草坪面积相比,结果是
A.保持不变 B.增加了 C.增加了 D.减少了
9.数形结合是初中数学重要的思想方法,下图就是用几何图形描述了一个重要的数学公式,这个公式是
A. B.
C. D.
10.如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪拼成一个矩形,通过计算两个图形阴影部分的面积,验证了一个等式,则这个等式是
A. B.
C. D.
二.填空题(共9小题)
11.计算: .
12.若,,则的值为 .
13.若是一个完全平方式,则 .
14.若,,则的值是 .
15.若,则的值是 .
16.已知,,则的值为 .
17.如果多项式加上一个单项式后能成为一个完全平方式,那么加上的这个单项式是 .(填一个即可).
18.用面积为的四个长方形拼成一个“回形”正方形如图所示,小正方形阴影部分的面积为16.则长方形的周长为 .
19.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长宽分别为2和1的长方形,现用甲类纸片1张,乙类纸片4张,丙类纸片若干张拼成一个新的大正方形,则至少需要丙类纸片 张.
三.解答题(共6小题)
20.化简:.
21.计算:.
22.若,,求的值.
23.已知,,求下列各式的值:
(1);
(2).
24.图①是一个长为,宽为的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积;
方法一: ;
方法二: ;
(2)观察图②,请直接写出下列三个代数式,,之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若,,求的值.
25.请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法 .
方法 .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为、,如果,求阴影部分的面积.
参考答案
一.选择题(共10小题)
1.下列式子中,能用平方差公式运算的是
A. B. C. D.
解:、中存在相同项,没有相反项,不能用平方差公式计算,故本选项不符合题意;
、两项都是相同,不能用平方差公式计算,故本选项不符合题意;
、存在相同的项与互为相反数的项,能用平方差公式计算,故本选项符合题意;
、中两项都是相反项,没有相同项,不能用平方差公式计算,故本选项不符合题意;
故选:.
2.计算的结果是
A. B. C. D.
解:原式
.
故选:.
3.为了运用平方差公式计算,下列变形正确的是
A. B.
C. D.
解:运用平方差公式计算,
应变形为,
故选:.
4.若,,求的值是
A.4 B. C.2 D.
解:,,
,
,
,
,
故选:.
5.关于的二次三项式是一个完全平方式,则的值应为
A. B. C. D.
解:是完全平方式,
,
.
故选:.
6.若,,则的值是
A.11 B.21 C.29 D.49
解:因为,,
所以;
故选:.
7.若,,则
A. B.3 C. D.4
解:,,
,
,
,
.
故选:.
8.为了美化城市,经统一规划,将一块正方形草坪的南北方向增加,东西方向减少,则改造后得到长方形草坪与原正方形草坪面积相比,结果是
A.保持不变 B.增加了 C.增加了 D.减少了
解:设正方形草坪的原边长为,则面积为;
将一正方形草坪的南北方向增加,东西方向缩短后,边长为,,
面积为.
故减少.
故选:.
9.数形结合是初中数学重要的思想方法,下图就是用几何图形描述了一个重要的数学公式,这个公式是
A. B.
C. D.
解:图1中阴影部分面积等于大正方形的面积,减去小正方形的面积,即;
图2中阴影部分为长等于,宽等于的长方形,其面积等于,
二者面积相等,则有.
比较各选项,可知只有符合题意.
故选:.
10.如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪拼成一个矩形,通过计算两个图形阴影部分的面积,验证了一个等式,则这个等式是
A. B.
C. D.
解:左图的阴影部分的面积为,右图的阴影部分的面积为,
因此有为,
故选:.
二.填空题(共9小题)
11.计算: .
解:.
故答案为:.
12.若,,则的值为 2 .
解:,,
.
故答案为:2.
13.若是一个完全平方式,则 12或 .
解:是一个完全平方式,
,
解得:或,
故答案为:12或.
14.若,,则的值是 2020 .
解:,,
.
故答案为2020.
15.若,则的值是 25 .
解:,
原式.
故答案为:25.
16.已知,,则的值为 25 .
解:,,
.
.
故答案是:25.
17.如果多项式加上一个单项式后能成为一个完全平方式,那么加上的这个单项式是 .(填一个即可).
解:,
即加上的这个单项式是,
故答案为:.
18.用面积为的四个长方形拼成一个“回形”正方形如图所示,小正方形阴影部分的面积为16.则长方形的周长为 10 .
解:由题意可得,,
,
,(舍去)
长方形的周长,
故答案为10.
19.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长宽分别为2和1的长方形,现用甲类纸片1张,乙类纸片4张,丙类纸片若干张拼成一个新的大正方形,则至少需要丙类纸片 4 张.
解:甲类纸片1张,乙类纸片4张,总面积是,大于8的完全平方数依次是9,16,,而丙的面积是2,因而不可能是9;
当总面积是16时,取的丙纸片的总面积是8,因而是4张.
因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.
故答案为:4.
三.解答题(共6小题)
20.化简:.
解:原式
.
21.计算:.
解:
.
22.若,,求的值.
解:把两边平方得:,即,
将代入得:,即,
则原式.
23.已知,,求下列各式的值:
(1);
(2).
解:(1)原式
;
(2)原式
.
24.图①是一个长为,宽为的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积;
方法一: ;
方法二: ;
(2)观察图②,请直接写出下列三个代数式,,之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若,,求的值.
解:(1)方法一:,
方法二:,
故答案为:;;
(2);
(3)当,时,.
25.请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法 .
方法 .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为、,如果,求阴影部分的面积.
解:(1)图1,两个阴影正方形的面积和:,
大正方形的面积减去两个长方形的面积:,
故答案为:,;
(2)两个数的平方和等于这两个数和的平方减去这两个数积的2倍,即:;
故答案为:;
(3)如图2,阴影部分的面积为:
.
_21?????????è?????(www.21cnjy.com)_
