人教版七年级上册数学 1.1 正数和负数 提高训练习题课件(2课时 共40张PPT)
文档属性
| 名称 | 人教版七年级上册数学 1.1 正数和负数 提高训练习题课件(2课时 共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 612.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览








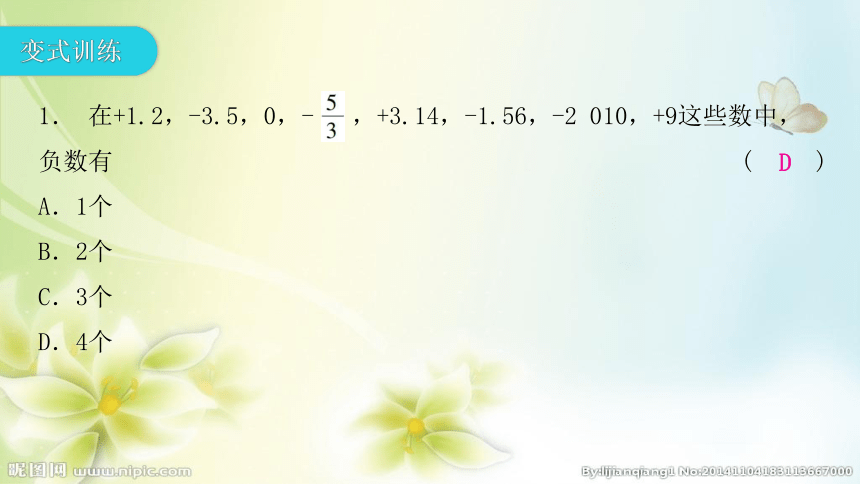


文档简介
(共40张PPT)
第一章
有理数
第1课时
正数和负数(1)
基础
知识思维导图
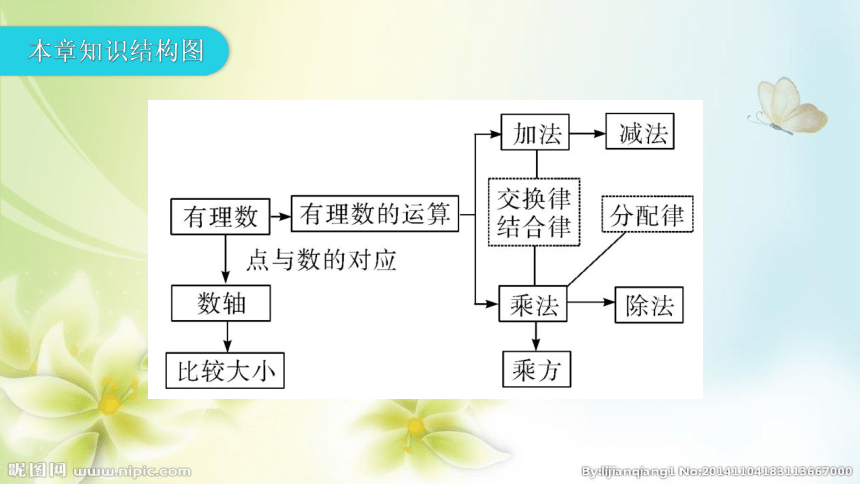
本章知识结构图
核心内容
有理数的分类及其相关概念
用正数和负数表示两种具有相反意义的量.0既不是正数,也不是负数.
整数和分数统称为有理数.有理数的分类:
有理数
整数
分数
正整数
0
负整数
正分数
负分数
有理数
正整数
0
负整数
正整数
正分数
负整数
负分数
有理数的分类及其相关概念
规定了原点、正方向和单位长度的直线叫做数轴.数轴的三要素:原点、单位长度、正方向.
只有符号不同的两个数叫做互为相反数.
数轴上表示某个数的点与原点的距离叫做这个数的绝对值.
a(a>0)
|a|=
0(a=0)
-a(a<0)
(1)互为相反数的两个数的绝对值相等;(2)绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数;(3)有理数的绝对值都是非负数.
有理数的分类及其相关概念
1.有理数的大小比较:比较有理数的大小可以利用数轴,它们从左到右的顺序,即从小到大的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.
2.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
有理数的运算
有理数加法法则:(1)同号相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,其中互为相反数的两个数相加得0;(3)一个数同0相加,仍得这个数.
交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c).
有理数减法法则:减去一个数,等于加这个数的相反数.
有理数的运算
1.有理数乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数同0相乘,都得0.
2.乘积是1的两个数互为倒数.
交换律:
ab=ba;结合律:(ab)c=a(bc);分配律:a(b+c)=
ab+ac.
有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数.
1.求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.科学记数法形式:±a×10n,其中1≤a<10,n为正整数.
3.
近似数与精确数的接近程度,可以用精确度表示,一般表述为“精确到哪一位”.
知识思维导图
知识点导学
A.
大于0的数叫做正数;在正数前面加上符号“-”(负)的数叫做负数;有时,在正数前面也加上“+”(正)号.一个数前面的“+”“-”号叫做它的符号.
0既不是正数,也不是负数.
1.在-7,-
,-23,0,
-1.8中,负数有________个.
B.
用正负数表示两种具有相反意义的量.
具有相反意义的量都是互相依存的两个量,它包含两个要素:一是它们的意义相反,二是它们都是数量.
2.若零上8
℃记作+8
℃,则零下5
℃记作________℃.
四
-5
典型例题
知识点1:负数
【例1】在-3,0,1,3这四个数中,负数是
(
)
A.-3
B.0
C.1
D.3
A
变式训练
1.
在+1.2,-3.5,0,-
,+3.14,-1.56,-2
010,+9这些数中,负数有
(
)
A.1个
B.2个
C.3个
D.4个
D
典型例题
知识点2:正数、负数与0
【例2】把下列各数填入相应的位置:3.4,
,-
,0.6,-8,-1.9,+11,-20,0.
正数:____________________________;
负数:____________________________;
既不是正数也不是负数:________.
3.4,
,0.6,+11
-
,-8,-1.9,-20
0
变式训练
2.
把下列各数填入相应的大括号里:-13.5,2,0,0.128,-2.236,3.14,+27,-
,-15%,
,
.
正数:{__________________________________…};
负数:{__________________________________…}.
2,0.128,3.14,+27,
,
,
-13.5,-2.236,-
,-15%,
典型例题
知识点3:用正负数表示相反意义的量
【例3】如果水位升高0.6
m时水位变化记作+0.6
m,那么水位下降0.8
m时水位变化记作
(
)
A.
0
m
B.
0.8
m
C.
-0.8
m
D.
-0.5
m
C
变式训练
3.用正数或负数表示下列各量:
(1)零上24
℃表示为________℃,
零下3.5
℃表示为________℃;
(2)足球比赛,赢2球可记作________球,
输1球可记作________球.
+24
-3.5
+2
-1
典型例题
知识点4:正负数的意义
【例4】如果收入用正数表示,支出用负数表示,那么-60元表示(
)
A.收入60元
B.支出60元
C.收入比支出多60元
D.收入比支出少60元
B
变式训练
4.
海水涨了-4
cm的意义是
(
)
A.海水涨了4
cm
B.海水下降了4
cm
C.海水水位没有变化
D.无法确定
B
分层训练
A组
5.
在0,1,-1,2中,是负数的是
(
)
A.0
B.1
C.-1
D.2
6.
下列各数中,为正数的是
(
)
A.
B.-
C.-4
D.0
C
A
7.
下面各数哪些是正数,哪些是负数?
+5,-40,89,0,-0.2,-5.4,+4,80,-120.
正数:_____________________________;
负数:_____________________________;
既不是正数也不是负数:________.
+5,89,+4,80
-40,-0.2,-5.4,-120
0
8.
在下列选项中,具有相反意义的量是
(
)
A.
胜2局与负3局
B.
盈利5万元与支出6万元
C.
气温升高3
℃与气温为-3
℃
D.
向东行20
m与向南行30
m
A
9.
用正负数表示下面的数量.
(1)如果向东走240
m记作+240
m,那么向西走200
m就记作________m;
(2)如果李伯伯在银行存入300元记作+300元,那么在银行取出100元就记作________元;
(3)如果汽车到站后下去10人记作-10人,那么上来20人就记作________人;
(4)世界上最高的淡水湖高于海平面3
812
m,记作__________m.
-200
-100
+20
+3
812
10.通常情况下,盈利用正数表示,亏损用负数表示,根据下面信息完成表格.
七月份:亏损1
200元;八月份:亏损850元;九月份:盈利2
500元;十月份:盈利4
300元;十一月份:盈利3
700元;十二月份:亏损250元.
月份
七月份
八月份
九月份
十月份
十一
月份
十二
月份
盈亏/
元
————
————
————
————
————
————
-1
200
-850
+2
500
+4
300
+3
700
-250
B组
11.
图1-1-1-1某人的微信钱包账单如图1-1-1-1,+5.20表示收入5.20元,下列说法正确的是
(
)
A.
-1.00表示收入1.00元
B.
-1.00表示支出1.00元
C.
-1.00表示支出-1.00元
D.
收支总和为6.20元
B
12.
2019年某省常住人口的增长率是-0.65‰,下列说法符合实际情况的是
(
)
A.
这个省的常住人口数是负数
B.
这个省的常住人口数呈增长趋势
C.
这个省的常住人口数呈下降趋势
D.
这个省的常住人口增长率是正数
C
C组
13.关于“零”的说法正确的是
(
)
①是整数,也是正数;
②不是正数,也不是负数;
③不是整数,是正数;
④是整数,也是自然数.
A.①④
B.②④
C.①②
D.①③
B
14.下面依次排列的一列数,它们的排列有一定的规律,请接着写出后面的三个数:
(1)1,-1,1,-1,________,________,________;
(2)-1,
,-
,
,________,________,________;
(3)
________,________,________.
1
-1
1
第2课时
正数和负数(2)——生活中的应用
知识思维导图
知识点导学
A.
一般用正数表示比标准值大的允许误差,用负数表示比标准值小的允许误差,即与标准值相比较,超出的部分为正,不足的部分为负,反之,借助正负数的意义也可以求出实际值.
1.
通常在生产图纸上,对每个产品的合格范围有明确的规定.
例如,图纸上注明一个零件的直径是
,表示这个零件直径的标准尺寸是30
mm,实际产品的直径最大可以是30.03
mm,最小可以是____________.
29.98
mm
典型例题
知识点1:
借助正负数表示范围
【例1】
某种药品的说明书上标明保存温度是(20±2)℃,则该药品在___________范围内保存才合适.
(
)
A.18℃~20℃
B.20℃~22℃
C.18℃~21℃
D.18℃~22℃
D
变式训练
1.
某药品包装盒上标注着“贮藏温度:1
℃±2
℃”,以下是几个保存柜的温度,适合贮藏这种药品的温度是
(
)
A.
-4
℃
B.
0
℃
C.
4
℃
D.
5
℃
B
典型例题
知识点2:
借助正负数选择最接近标准的
【例2】
某排球队检测排球,其中质量超过标准的克数记为正数,不足的克数记为负数.
下面是检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是
(
)
A
变式训练
2.
下表是国外城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数).
那么与北京时间最接近的城市是
(
)
A.
伦敦
B.
墨尔本
C.
东京
D.
巴黎
C
城市
伦敦
墨尔本
东京
巴黎
时差/时
-8
+3
+1
-7
典型例题
知识点3:
选取某数做标准,用正负数表示其他数
【例3】人体正常体温平均为36.5
℃,如果高出的部分记为正,低于的部分记为负,某同学在家测的体温为38
℃,应记为__________.
1.5
℃
变式训练
3.
六(1)班数学平均分是88分,王莉考了95分,记作+7分;刘乐乐考了80分,应记作________分;李晓梅的成绩记作-5分,她考了________分.
-8
83
分层训练
A组
4.
检测4袋茶叶的质量,超过标准的克数记为正数,不足的克数记为负数,从重量的角度来看,最接近标准的那一袋是
(
)
A.
+3
B.
-0.3
C.
+0.2
D.
-3.6
5.
某种药品的说明书上标有保存温度是(20±2)℃,请你写出适合该药品保存的温度范围:___________________.
C
18
℃~22
℃
6.
若把37
℃记作0,超过37
℃的部分记为正,则-0.5
℃表示(
)
A.
零上0.5
℃
B.
零下0.5
℃
C.
36.5
℃
D.
37.5
℃
7.
超市某品牌食品包装袋上“质量”标注:500
g±20
g.下列待检查的四袋食品中,质量合格的是
(
)
A.530
g
B.519
g
C.470
g
D.459
g
C
B
B组
8.
设置一种记分数的方法:85分以上如88分记为+3分,某个学生的分数在记分表上记为-6分,则这个学生的分数应该是分.
(
)
A.
91
B.
-91
C.
79
D.
-79
9.
一袋大米的标准重量为25
kg,把一袋重25.5
kg的大米记为+0.5
kg,则一袋重24.8
kg的大米记为
(
)
A.
-9.8
kg
B.
+9.8
kg
C.
-0.2
kg
D.
0.2
kg
C
C
10.
渥太华与北京的时差为-13时(正数表示同一时刻比北京早的时数),如果北京时间为12月25日10:00,那么渥太华时间为
(
)
A.
12月25日23时
B.
12月25日21时
C.
12月24日21时
D.
12月24日9时
C
11.
开学时体育老师对班上的男同学进行了单杠引体向上的测验,以能做7次为标准,超过的次数用正数表示,不足的次数用负数表示,第一小组8名男同学的成绩如下表:
则第一小组达标的男同学有
(
)
A.
3名
B.
4名
C.
5名
D.
6名
C
学生序号
1
2
3
4
5
6
7
8
成绩
2
-1
0
3
-2
-3
1
0
C组
12.
某水泥厂计划每月生产水泥1
000
t,一月份实际生产了950
t,二月份实际生产了1
000
t,三月份实际生产了1
100
t,用正数和负数表示每月超额完成计划的吨数各是多少?
解:一月份超额完成计划-50
t,二月份超额完成计划0
t,三月份超额完成计划100
t.
13.
某超市购进一批大米,大米的标准包装为每袋30
kg,售货员任选6袋进行了称重检验,超过标准重量的记作“+”,不足标准重量的记作“-”,他记录的结果是+0.5,-0.5,0,-0.5,-0.5,+1,求这6袋大米的总重量.
解:30.5+29.5+30+29.5+29.5+31=180(kg).
答:这6袋大米的总重量为180
kg.
第一章
有理数
第1课时
正数和负数(1)
基础
知识思维导图
本章知识结构图
核心内容
有理数的分类及其相关概念
用正数和负数表示两种具有相反意义的量.0既不是正数,也不是负数.
整数和分数统称为有理数.有理数的分类:
有理数
整数
分数
正整数
0
负整数
正分数
负分数
有理数
正整数
0
负整数
正整数
正分数
负整数
负分数
有理数的分类及其相关概念
规定了原点、正方向和单位长度的直线叫做数轴.数轴的三要素:原点、单位长度、正方向.
只有符号不同的两个数叫做互为相反数.
数轴上表示某个数的点与原点的距离叫做这个数的绝对值.
a(a>0)
|a|=
0(a=0)
-a(a<0)
(1)互为相反数的两个数的绝对值相等;(2)绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数;(3)有理数的绝对值都是非负数.
有理数的分类及其相关概念
1.有理数的大小比较:比较有理数的大小可以利用数轴,它们从左到右的顺序,即从小到大的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.
2.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
有理数的运算
有理数加法法则:(1)同号相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,其中互为相反数的两个数相加得0;(3)一个数同0相加,仍得这个数.
交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c).
有理数减法法则:减去一个数,等于加这个数的相反数.
有理数的运算
1.有理数乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数同0相乘,都得0.
2.乘积是1的两个数互为倒数.
交换律:
ab=ba;结合律:(ab)c=a(bc);分配律:a(b+c)=
ab+ac.
有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数.
1.求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.科学记数法形式:±a×10n,其中1≤a<10,n为正整数.
3.
近似数与精确数的接近程度,可以用精确度表示,一般表述为“精确到哪一位”.
知识思维导图
知识点导学
A.
大于0的数叫做正数;在正数前面加上符号“-”(负)的数叫做负数;有时,在正数前面也加上“+”(正)号.一个数前面的“+”“-”号叫做它的符号.
0既不是正数,也不是负数.
1.在-7,-
,-23,0,
-1.8中,负数有________个.
B.
用正负数表示两种具有相反意义的量.
具有相反意义的量都是互相依存的两个量,它包含两个要素:一是它们的意义相反,二是它们都是数量.
2.若零上8
℃记作+8
℃,则零下5
℃记作________℃.
四
-5
典型例题
知识点1:负数
【例1】在-3,0,1,3这四个数中,负数是
(
)
A.-3
B.0
C.1
D.3
A
变式训练
1.
在+1.2,-3.5,0,-
,+3.14,-1.56,-2
010,+9这些数中,负数有
(
)
A.1个
B.2个
C.3个
D.4个
D
典型例题
知识点2:正数、负数与0
【例2】把下列各数填入相应的位置:3.4,
,-
,0.6,-8,-1.9,+11,-20,0.
正数:____________________________;
负数:____________________________;
既不是正数也不是负数:________.
3.4,
,0.6,+11
-
,-8,-1.9,-20
0
变式训练
2.
把下列各数填入相应的大括号里:-13.5,2,0,0.128,-2.236,3.14,+27,-
,-15%,
,
.
正数:{__________________________________…};
负数:{__________________________________…}.
2,0.128,3.14,+27,
,
,
-13.5,-2.236,-
,-15%,
典型例题
知识点3:用正负数表示相反意义的量
【例3】如果水位升高0.6
m时水位变化记作+0.6
m,那么水位下降0.8
m时水位变化记作
(
)
A.
0
m
B.
0.8
m
C.
-0.8
m
D.
-0.5
m
C
变式训练
3.用正数或负数表示下列各量:
(1)零上24
℃表示为________℃,
零下3.5
℃表示为________℃;
(2)足球比赛,赢2球可记作________球,
输1球可记作________球.
+24
-3.5
+2
-1
典型例题
知识点4:正负数的意义
【例4】如果收入用正数表示,支出用负数表示,那么-60元表示(
)
A.收入60元
B.支出60元
C.收入比支出多60元
D.收入比支出少60元
B
变式训练
4.
海水涨了-4
cm的意义是
(
)
A.海水涨了4
cm
B.海水下降了4
cm
C.海水水位没有变化
D.无法确定
B
分层训练
A组
5.
在0,1,-1,2中,是负数的是
(
)
A.0
B.1
C.-1
D.2
6.
下列各数中,为正数的是
(
)
A.
B.-
C.-4
D.0
C
A
7.
下面各数哪些是正数,哪些是负数?
+5,-40,89,0,-0.2,-5.4,+4,80,-120.
正数:_____________________________;
负数:_____________________________;
既不是正数也不是负数:________.
+5,89,+4,80
-40,-0.2,-5.4,-120
0
8.
在下列选项中,具有相反意义的量是
(
)
A.
胜2局与负3局
B.
盈利5万元与支出6万元
C.
气温升高3
℃与气温为-3
℃
D.
向东行20
m与向南行30
m
A
9.
用正负数表示下面的数量.
(1)如果向东走240
m记作+240
m,那么向西走200
m就记作________m;
(2)如果李伯伯在银行存入300元记作+300元,那么在银行取出100元就记作________元;
(3)如果汽车到站后下去10人记作-10人,那么上来20人就记作________人;
(4)世界上最高的淡水湖高于海平面3
812
m,记作__________m.
-200
-100
+20
+3
812
10.通常情况下,盈利用正数表示,亏损用负数表示,根据下面信息完成表格.
七月份:亏损1
200元;八月份:亏损850元;九月份:盈利2
500元;十月份:盈利4
300元;十一月份:盈利3
700元;十二月份:亏损250元.
月份
七月份
八月份
九月份
十月份
十一
月份
十二
月份
盈亏/
元
————
————
————
————
————
————
-1
200
-850
+2
500
+4
300
+3
700
-250
B组
11.
图1-1-1-1某人的微信钱包账单如图1-1-1-1,+5.20表示收入5.20元,下列说法正确的是
(
)
A.
-1.00表示收入1.00元
B.
-1.00表示支出1.00元
C.
-1.00表示支出-1.00元
D.
收支总和为6.20元
B
12.
2019年某省常住人口的增长率是-0.65‰,下列说法符合实际情况的是
(
)
A.
这个省的常住人口数是负数
B.
这个省的常住人口数呈增长趋势
C.
这个省的常住人口数呈下降趋势
D.
这个省的常住人口增长率是正数
C
C组
13.关于“零”的说法正确的是
(
)
①是整数,也是正数;
②不是正数,也不是负数;
③不是整数,是正数;
④是整数,也是自然数.
A.①④
B.②④
C.①②
D.①③
B
14.下面依次排列的一列数,它们的排列有一定的规律,请接着写出后面的三个数:
(1)1,-1,1,-1,________,________,________;
(2)-1,
,-
,
,________,________,________;
(3)
________,________,________.
1
-1
1
第2课时
正数和负数(2)——生活中的应用
知识思维导图
知识点导学
A.
一般用正数表示比标准值大的允许误差,用负数表示比标准值小的允许误差,即与标准值相比较,超出的部分为正,不足的部分为负,反之,借助正负数的意义也可以求出实际值.
1.
通常在生产图纸上,对每个产品的合格范围有明确的规定.
例如,图纸上注明一个零件的直径是
,表示这个零件直径的标准尺寸是30
mm,实际产品的直径最大可以是30.03
mm,最小可以是____________.
29.98
mm
典型例题
知识点1:
借助正负数表示范围
【例1】
某种药品的说明书上标明保存温度是(20±2)℃,则该药品在___________范围内保存才合适.
(
)
A.18℃~20℃
B.20℃~22℃
C.18℃~21℃
D.18℃~22℃
D
变式训练
1.
某药品包装盒上标注着“贮藏温度:1
℃±2
℃”,以下是几个保存柜的温度,适合贮藏这种药品的温度是
(
)
A.
-4
℃
B.
0
℃
C.
4
℃
D.
5
℃
B
典型例题
知识点2:
借助正负数选择最接近标准的
【例2】
某排球队检测排球,其中质量超过标准的克数记为正数,不足的克数记为负数.
下面是检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是
(
)
A
变式训练
2.
下表是国外城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数).
那么与北京时间最接近的城市是
(
)
A.
伦敦
B.
墨尔本
C.
东京
D.
巴黎
C
城市
伦敦
墨尔本
东京
巴黎
时差/时
-8
+3
+1
-7
典型例题
知识点3:
选取某数做标准,用正负数表示其他数
【例3】人体正常体温平均为36.5
℃,如果高出的部分记为正,低于的部分记为负,某同学在家测的体温为38
℃,应记为__________.
1.5
℃
变式训练
3.
六(1)班数学平均分是88分,王莉考了95分,记作+7分;刘乐乐考了80分,应记作________分;李晓梅的成绩记作-5分,她考了________分.
-8
83
分层训练
A组
4.
检测4袋茶叶的质量,超过标准的克数记为正数,不足的克数记为负数,从重量的角度来看,最接近标准的那一袋是
(
)
A.
+3
B.
-0.3
C.
+0.2
D.
-3.6
5.
某种药品的说明书上标有保存温度是(20±2)℃,请你写出适合该药品保存的温度范围:___________________.
C
18
℃~22
℃
6.
若把37
℃记作0,超过37
℃的部分记为正,则-0.5
℃表示(
)
A.
零上0.5
℃
B.
零下0.5
℃
C.
36.5
℃
D.
37.5
℃
7.
超市某品牌食品包装袋上“质量”标注:500
g±20
g.下列待检查的四袋食品中,质量合格的是
(
)
A.530
g
B.519
g
C.470
g
D.459
g
C
B
B组
8.
设置一种记分数的方法:85分以上如88分记为+3分,某个学生的分数在记分表上记为-6分,则这个学生的分数应该是分.
(
)
A.
91
B.
-91
C.
79
D.
-79
9.
一袋大米的标准重量为25
kg,把一袋重25.5
kg的大米记为+0.5
kg,则一袋重24.8
kg的大米记为
(
)
A.
-9.8
kg
B.
+9.8
kg
C.
-0.2
kg
D.
0.2
kg
C
C
10.
渥太华与北京的时差为-13时(正数表示同一时刻比北京早的时数),如果北京时间为12月25日10:00,那么渥太华时间为
(
)
A.
12月25日23时
B.
12月25日21时
C.
12月24日21时
D.
12月24日9时
C
11.
开学时体育老师对班上的男同学进行了单杠引体向上的测验,以能做7次为标准,超过的次数用正数表示,不足的次数用负数表示,第一小组8名男同学的成绩如下表:
则第一小组达标的男同学有
(
)
A.
3名
B.
4名
C.
5名
D.
6名
C
学生序号
1
2
3
4
5
6
7
8
成绩
2
-1
0
3
-2
-3
1
0
C组
12.
某水泥厂计划每月生产水泥1
000
t,一月份实际生产了950
t,二月份实际生产了1
000
t,三月份实际生产了1
100
t,用正数和负数表示每月超额完成计划的吨数各是多少?
解:一月份超额完成计划-50
t,二月份超额完成计划0
t,三月份超额完成计划100
t.
13.
某超市购进一批大米,大米的标准包装为每袋30
kg,售货员任选6袋进行了称重检验,超过标准重量的记作“+”,不足标准重量的记作“-”,他记录的结果是+0.5,-0.5,0,-0.5,-0.5,+1,求这6袋大米的总重量.
解:30.5+29.5+30+29.5+29.5+31=180(kg).
答:这6袋大米的总重量为180
kg.
