五年级上册数学课件-9.1 鸡兔同笼 冀教版 (共21张PPT) (1)
文档属性
| 名称 | 五年级上册数学课件-9.1 鸡兔同笼 冀教版 (共21张PPT) (1) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 00:00:00 | ||
图片预览







文档简介
鸡 兔 同 笼
鸡兔同笼、韩信点兵、李白买酒被称为我国古代三大趣题,它被记载于《孙子算经》一书中,距今已有1500多年。
大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题,这就是著名的“鸡兔同笼”问题。
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
这道题的意思是:
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
鸡有几条腿?
兔有几条腿?
猜一猜:各有多少只?
鸡兔同笼,有8个头,26只脚,鸡兔各多少只?
化繁为简:
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
笼子里有若干只鸡和兔.从上面数,有8个头,
从下面数,有26只脚.鸡和兔各有几只?
活动要求:
(1)可借助列表格、画图、列算式等方法独立解决问题。
(2)完成后组内交流方法。
鸡/只
兔/只
脚/只
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
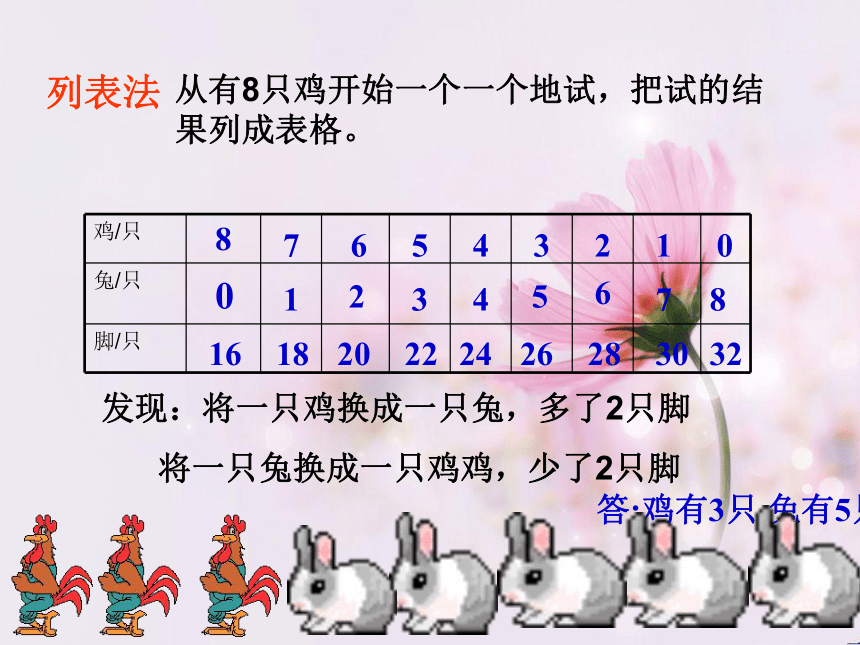
答:鸡有3只,兔有5只.
列表法
从有8只鸡开始一个一个地试,把试的结果列成表格。
发现:将一只鸡换成一只兔,多了2只脚
将一只兔换成一只鸡鸡,少了2只脚
3只鸡,5只兔。
鸡/只
兔/只
脚/只
我是跳跃列举
怎样才能更快的找到结果?
先假设鸡和兔各占一半,再列表。
3只鸡,5只兔。
怎样才能更快的找到结果?
鸡/只
兔/只
脚/只
4
4
24
3
5
26
用画图的方法试一试。
…
先画8个圆圈表示8个头。
再为每条动物画两只脚,8只动物只用完16只脚,还多出10只脚。
…
把剩下的10只脚用完,要给其中的5只动物各添2只脚,这5只就是兔子,另外的3只就是鸡。
…
图示法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
2×8=16(只)
比较 26-16=10(只)
假设法1:
推算 10÷2=5(只)
8-5=3(只)
答:鸡有3只,兔有5只。
兔子:
小鸡:
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
答:鸡有3只,兔有5只。
假设法2:
8×4=32(只)
比较 32-26=6(只)
推算 6÷2=3(只)
8-3=5(只)
兔子:
小鸡:
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
龟鹤共40只,有112条腿。龟、鹤各有多少只?
想一想
小明的储蓄罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
1角/枚
5角/枚
总价值/元
……
……
……
拓展思路:(一)抬腿法
假设这些鸡和兔全都接受训练,每吹一次口哨便抬起一条腿。
先吹一次,所有鸡和兔都抬起一条腿,那就还剩94-36=59(条)腿。
再吹一次,所有鸡和兔又抬起一条腿,那么还剩59-35=24(条)腿。
现在,我们会发现鸡的2条腿全部抬起,坐在地上了,剩下的腿全是兔子的腿了,每只兔子只剩下2条腿,所以24÷2=12(只)——兔子;
35-12=23(只)——鸡。
(二)介绍《孙子算经》中的算法(减半法)
(1)假如让鸡抬起一只脚,兔子抬起两只脚,相当于脚数
去掉了一半,还有 94÷2=47只脚。
(2)这时,每只鸡一只脚,每只兔子两只脚。笼子里只要
有一只兔子,则脚的总数就比头的总数多1。
(3)这时脚的总数与头的总数之差 47-35=12,就是兔子
的只数。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,
有94只脚。鸡和兔各有几只?
古人的算法是让头的数量和脚的数量对应起来进行思考。
( )
( )
( )
( )
古人的算法可以用下图表示:
头… 35 35 35 23 …鸡
脚… 94 47 12 12 …兔
下减上
脚减半
上减下
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
(三)用方程解:
解:设有x只兔,那么就有(8-x)只鸡。
兔脚的总只数+鸡脚的总只数=26只
4x+2(8-x)=26
4x+16-2x=26
2x+16=26
2x=26-16
2x=10
X=5
8-5=3(只)
答:兔有5只,鸡有3只。
解决鸡兔同笼除了上述方法外,我们还可以用面积法
谢 谢
鸡兔同笼、韩信点兵、李白买酒被称为我国古代三大趣题,它被记载于《孙子算经》一书中,距今已有1500多年。
大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题,这就是著名的“鸡兔同笼”问题。
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
这道题的意思是:
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
鸡有几条腿?
兔有几条腿?
猜一猜:各有多少只?
鸡兔同笼,有8个头,26只脚,鸡兔各多少只?
化繁为简:
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
笼子里有若干只鸡和兔.从上面数,有8个头,
从下面数,有26只脚.鸡和兔各有几只?
活动要求:
(1)可借助列表格、画图、列算式等方法独立解决问题。
(2)完成后组内交流方法。
鸡/只
兔/只
脚/只
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
答:鸡有3只,兔有5只.
列表法
从有8只鸡开始一个一个地试,把试的结果列成表格。
发现:将一只鸡换成一只兔,多了2只脚
将一只兔换成一只鸡鸡,少了2只脚
3只鸡,5只兔。
鸡/只
兔/只
脚/只
我是跳跃列举
怎样才能更快的找到结果?
先假设鸡和兔各占一半,再列表。
3只鸡,5只兔。
怎样才能更快的找到结果?
鸡/只
兔/只
脚/只
4
4
24
3
5
26
用画图的方法试一试。
…
先画8个圆圈表示8个头。
再为每条动物画两只脚,8只动物只用完16只脚,还多出10只脚。
…
把剩下的10只脚用完,要给其中的5只动物各添2只脚,这5只就是兔子,另外的3只就是鸡。
…
图示法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
2×8=16(只)
比较 26-16=10(只)
假设法1:
推算 10÷2=5(只)
8-5=3(只)
答:鸡有3只,兔有5只。
兔子:
小鸡:
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
答:鸡有3只,兔有5只。
假设法2:
8×4=32(只)
比较 32-26=6(只)
推算 6÷2=3(只)
8-3=5(只)
兔子:
小鸡:
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
龟鹤共40只,有112条腿。龟、鹤各有多少只?
想一想
小明的储蓄罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
1角/枚
5角/枚
总价值/元
……
……
……
拓展思路:(一)抬腿法
假设这些鸡和兔全都接受训练,每吹一次口哨便抬起一条腿。
先吹一次,所有鸡和兔都抬起一条腿,那就还剩94-36=59(条)腿。
再吹一次,所有鸡和兔又抬起一条腿,那么还剩59-35=24(条)腿。
现在,我们会发现鸡的2条腿全部抬起,坐在地上了,剩下的腿全是兔子的腿了,每只兔子只剩下2条腿,所以24÷2=12(只)——兔子;
35-12=23(只)——鸡。
(二)介绍《孙子算经》中的算法(减半法)
(1)假如让鸡抬起一只脚,兔子抬起两只脚,相当于脚数
去掉了一半,还有 94÷2=47只脚。
(2)这时,每只鸡一只脚,每只兔子两只脚。笼子里只要
有一只兔子,则脚的总数就比头的总数多1。
(3)这时脚的总数与头的总数之差 47-35=12,就是兔子
的只数。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,
有94只脚。鸡和兔各有几只?
古人的算法是让头的数量和脚的数量对应起来进行思考。
( )
( )
( )
( )
古人的算法可以用下图表示:
头… 35 35 35 23 …鸡
脚… 94 47 12 12 …兔
下减上
脚减半
上减下
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
(三)用方程解:
解:设有x只兔,那么就有(8-x)只鸡。
兔脚的总只数+鸡脚的总只数=26只
4x+2(8-x)=26
4x+16-2x=26
2x+16=26
2x=26-16
2x=10
X=5
8-5=3(只)
答:兔有5只,鸡有3只。
解决鸡兔同笼除了上述方法外,我们还可以用面积法
谢 谢
