湘教版数学九年级下册2.6 弧长与扇形面积教学课件(共32张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.6 弧长与扇形面积教学课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
弧长与扇形面积
教学课件
湘教版九年级下册
01
新课导入
新课导入
如图是某城市摩天轮的图片,点O是圆心,半径r=15cm,点A,B是圆上的两点,圆心角∠AOB=120°,你能想办法求出AB的长度么?说说你的理由.
⌒
O
B
A
120°
02
新知探究
新知探究
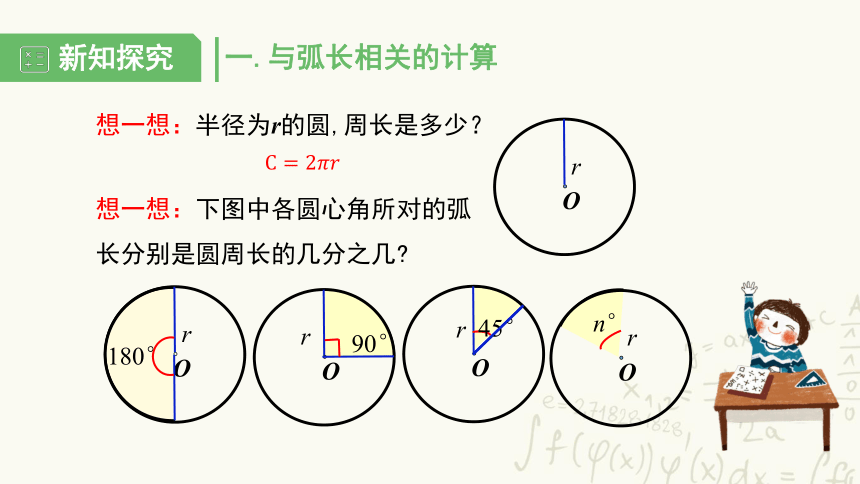
一.与弧长相关的计算
想一想:半径为r的圆,周长是多少?
O
r
想一想:下图中各圆心角所对的弧长分别是圆周长的几分之几?
O
r
180°
O
r
90°
O
r
45°
O
r
n°
新知探究
(1)
圆心角是180°,占整个周角的
,因此它所对的弧长是圆周长的__________.
(2)
圆心角是90°,占整个周角的
,因此它所对的弧长是圆周长的__________.
(3)
圆心角是45°,占整个周角的
,因此它所对的弧长是圆周长的__________.
(4)
圆心角是n°,占整个周角的
,因此它所对的弧长是圆周长的__________.
新知探究
归纳总结
(1)用弧长公式
进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,而只有在同圆或等圆中,才可能是等弧.
注意
弧长公式
半径为r的圆中,n°的圆心角所对的弧长l为
·2r
新知探究
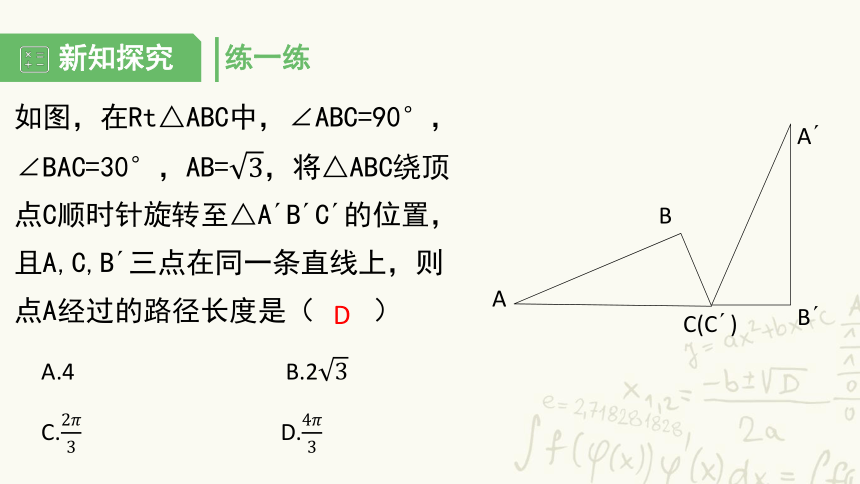
练一练
如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=,将△ABC绕顶点C顺时针旋转至△A?B?C?的位置,且A,C,B?三点在同一条直线上,则点A经过的路径长度是(
)
A?
B?
C(C?)
B
A
A.4
B.2
C.
D.
D
新知探究
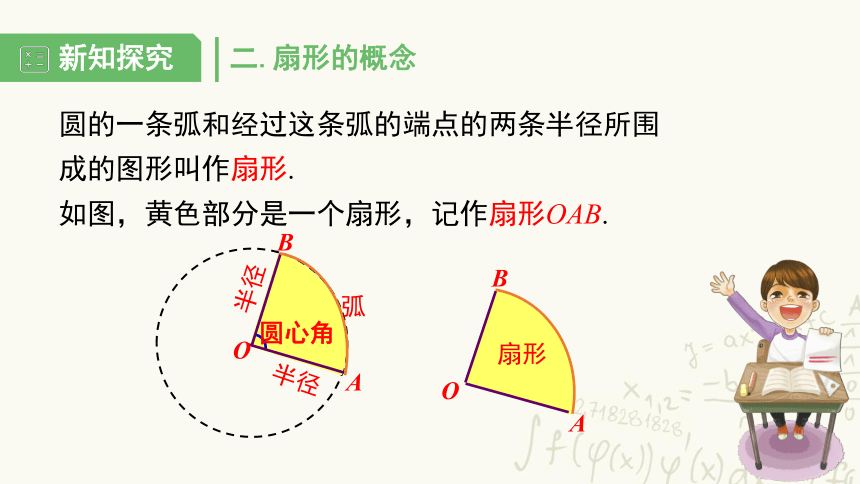
二.扇形的概念
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
新知探究
三.扇形面积的计算
半径为r的圆,面积是多少?
O
r
下图中各扇形面积分别是圆面积的几分之几,具体是多少呢?
S
新知探究
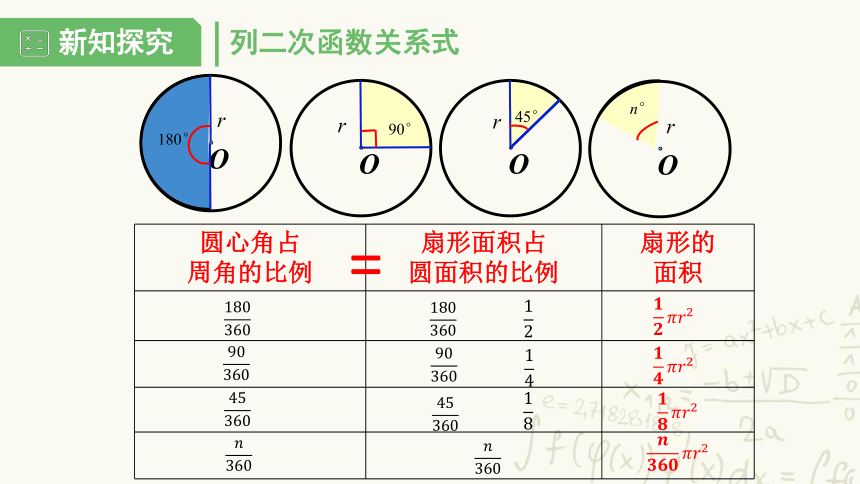
列二次函数关系式
圆心角占
周角的比例
扇形面积占
圆面积的比例
扇形的
面积
=
O
r
180°
O
r
90°
O
r
45°
O
r
n°
新知探究
归纳总结
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
新知探究
三.扇形面积的计算
______大小不变时,对应的扇形面积与______有关,
_________越长,面积越大.
圆心角
半径
半径
圆的
不变时,扇形面积与
有关,
越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O
●
A
B
D
C
E
F
O
●
A
B
C
D
想一想:扇形的面积与哪些因素有关?
新知探究
练一练
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是(
)
O
●
A
B
D
C
P
A.
B.
C.
D.
C
新知探究
归纳总结
求扇形面积的方法:
(1)当已知圆心角的度数时,选用公式;
(2)当已知弧长时,选用公式
新知探究
小对比
想一想:扇形的弧长公式与面积公式有联系吗?
想一想:扇形的面积公式与什么公式类似?
A
B
O
O
新知探究
知识拓展
左图:
S弓形=S扇形-S三角形
右图:S弓形=S扇形+S三角形
O
O
弓形的面积=扇形的面积±三角形的面积
弓形面积公式
03
典型例题
典型例题
1.120°的圆心角所对的弧长是6,则此弧所在的圆的半径是(
)
A.3
B.
4
C.9
D.18
C
典型例题
2.如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是(
??)????
A.??????B.
?????C.??????D.2?
B
O
D
C
B
A
典型例题
3.如图,AB是⊙O的直径,点D为⊙O上的一点,且∠ABD=30°,BO=4,则BD的长为(
)
D
B
A
O
⌒
A.??????B.
?????
C.?????
D.
D
典型例题
4.如图,AB是⊙O的切线,切点为A,OB交⊙O于C,且C为OB的中点,过C点的弦CD使∠ACD=45°,AD的长为,求弦AD,AC的长.
⌒
O
D
C
B
A
AD=2;AC=
典型例题
解:
如图,连接OA,OD.
∵∠DCA=45°,
∴∠AOD=90°,
∴
AD的长为=,
∴OA=OD=,
∴AD==2,
∵AB是⊙O的切线,
∴OA⊥AB,
∴C为Rt△AOB斜边的中点,
∴AC=OC=OA=.
⌒
O
D
C
B
A
04
拓展提高
拓展提高
如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6cm,AB=6cm.求:
(1)⊙O的半径;
(2)图中阴影部分的面积.
O
D
B
C
A
3cm
()(cm2)
拓展提高
解:
(1)如图,连接OC,则OC⊥AB,
又∵OA=OB,
∴AC=BC=AB=3(cm).
在Rt△AOC中,
OC==3(cm),
∴
⊙O的半径为3cm.
O
D
B
C
A
拓展提高
(2)
∵OC=OB,
∴∠B=30°,∠COD=60°,
∴
S扇形OCD==(cm2),
∴阴影部分的面积为OC·CB-=()(cm2).
O
D
B
C
A
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
弧长与扇形面积
教学课件
湘教版九年级下册
01
新课导入
新课导入
如图是某城市摩天轮的图片,点O是圆心,半径r=15cm,点A,B是圆上的两点,圆心角∠AOB=120°,你能想办法求出AB的长度么?说说你的理由.
⌒
O
B
A
120°
02
新知探究
新知探究
一.与弧长相关的计算
想一想:半径为r的圆,周长是多少?
O
r
想一想:下图中各圆心角所对的弧长分别是圆周长的几分之几?
O
r
180°
O
r
90°
O
r
45°
O
r
n°
新知探究
(1)
圆心角是180°,占整个周角的
,因此它所对的弧长是圆周长的__________.
(2)
圆心角是90°,占整个周角的
,因此它所对的弧长是圆周长的__________.
(3)
圆心角是45°,占整个周角的
,因此它所对的弧长是圆周长的__________.
(4)
圆心角是n°,占整个周角的
,因此它所对的弧长是圆周长的__________.
新知探究
归纳总结
(1)用弧长公式
进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,而只有在同圆或等圆中,才可能是等弧.
注意
弧长公式
半径为r的圆中,n°的圆心角所对的弧长l为
·2r
新知探究
练一练
如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=,将△ABC绕顶点C顺时针旋转至△A?B?C?的位置,且A,C,B?三点在同一条直线上,则点A经过的路径长度是(
)
A?
B?
C(C?)
B
A
A.4
B.2
C.
D.
D
新知探究
二.扇形的概念
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
新知探究
三.扇形面积的计算
半径为r的圆,面积是多少?
O
r
下图中各扇形面积分别是圆面积的几分之几,具体是多少呢?
S
新知探究
列二次函数关系式
圆心角占
周角的比例
扇形面积占
圆面积的比例
扇形的
面积
=
O
r
180°
O
r
90°
O
r
45°
O
r
n°
新知探究
归纳总结
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
新知探究
三.扇形面积的计算
______大小不变时,对应的扇形面积与______有关,
_________越长,面积越大.
圆心角
半径
半径
圆的
不变时,扇形面积与
有关,
越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O
●
A
B
D
C
E
F
O
●
A
B
C
D
想一想:扇形的面积与哪些因素有关?
新知探究
练一练
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是(
)
O
●
A
B
D
C
P
A.
B.
C.
D.
C
新知探究
归纳总结
求扇形面积的方法:
(1)当已知圆心角的度数时,选用公式;
(2)当已知弧长时,选用公式
新知探究
小对比
想一想:扇形的弧长公式与面积公式有联系吗?
想一想:扇形的面积公式与什么公式类似?
A
B
O
O
新知探究
知识拓展
左图:
S弓形=S扇形-S三角形
右图:S弓形=S扇形+S三角形
O
O
弓形的面积=扇形的面积±三角形的面积
弓形面积公式
03
典型例题
典型例题
1.120°的圆心角所对的弧长是6,则此弧所在的圆的半径是(
)
A.3
B.
4
C.9
D.18
C
典型例题
2.如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是(
??)????
A.??????B.
?????C.??????D.2?
B
O
D
C
B
A
典型例题
3.如图,AB是⊙O的直径,点D为⊙O上的一点,且∠ABD=30°,BO=4,则BD的长为(
)
D
B
A
O
⌒
A.??????B.
?????
C.?????
D.
D
典型例题
4.如图,AB是⊙O的切线,切点为A,OB交⊙O于C,且C为OB的中点,过C点的弦CD使∠ACD=45°,AD的长为,求弦AD,AC的长.
⌒
O
D
C
B
A
AD=2;AC=
典型例题
解:
如图,连接OA,OD.
∵∠DCA=45°,
∴∠AOD=90°,
∴
AD的长为=,
∴OA=OD=,
∴AD==2,
∵AB是⊙O的切线,
∴OA⊥AB,
∴C为Rt△AOB斜边的中点,
∴AC=OC=OA=.
⌒
O
D
C
B
A
04
拓展提高
拓展提高
如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6cm,AB=6cm.求:
(1)⊙O的半径;
(2)图中阴影部分的面积.
O
D
B
C
A
3cm
()(cm2)
拓展提高
解:
(1)如图,连接OC,则OC⊥AB,
又∵OA=OB,
∴AC=BC=AB=3(cm).
在Rt△AOC中,
OC==3(cm),
∴
⊙O的半径为3cm.
O
D
B
C
A
拓展提高
(2)
∵OC=OB,
∴∠B=30°,∠COD=60°,
∴
S扇形OCD==(cm2),
∴阴影部分的面积为OC·CB-=()(cm2).
O
D
B
C
A
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
