湘教版数学九年级下册2.5.4 三角形内切圆教学课件(共33张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.4 三角形内切圆教学课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 23:40:51 | ||
图片预览




文档简介
(共33张PPT)
三角形的内切圆
教学课件
湘教版九年级下册
01
新课导入
新课导入
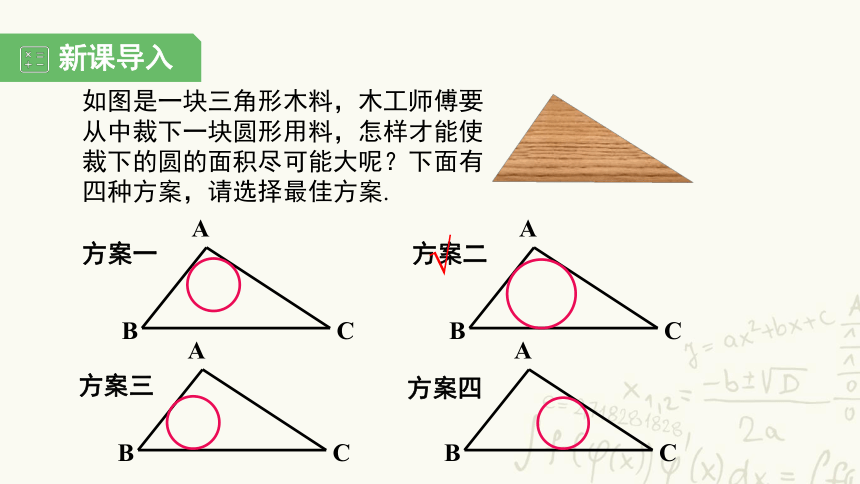
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?下面有四种方案,请选择最佳方案.
A
B
C
A
B
C
A
B
C
A
B
C
方案一
方案二
方案三
方案四
√
新课导入
同学们知道这是为什么吗?今天就让我们一起来探究一下!
02
新知探究
新知探究
一.三角形的内切圆
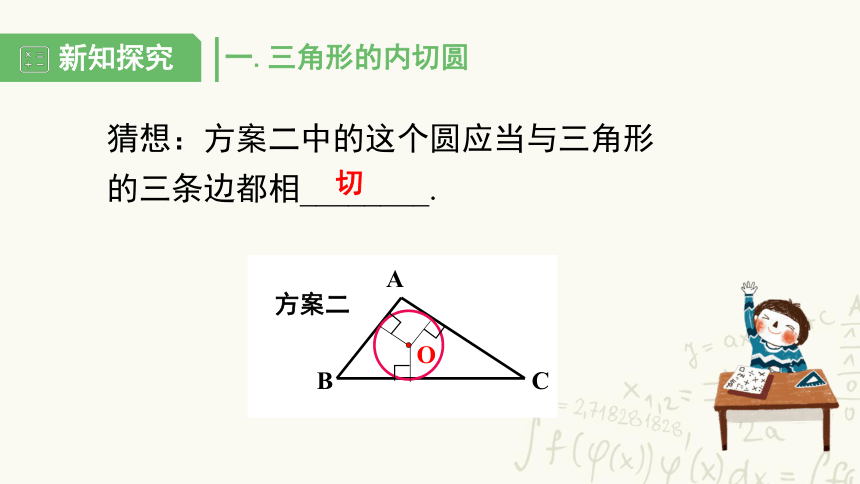
猜想:方案二中的这个圆应当与三角形的三条边都相________.
A
B
C
方案二
切
∟
∟
∟
O
新知探究
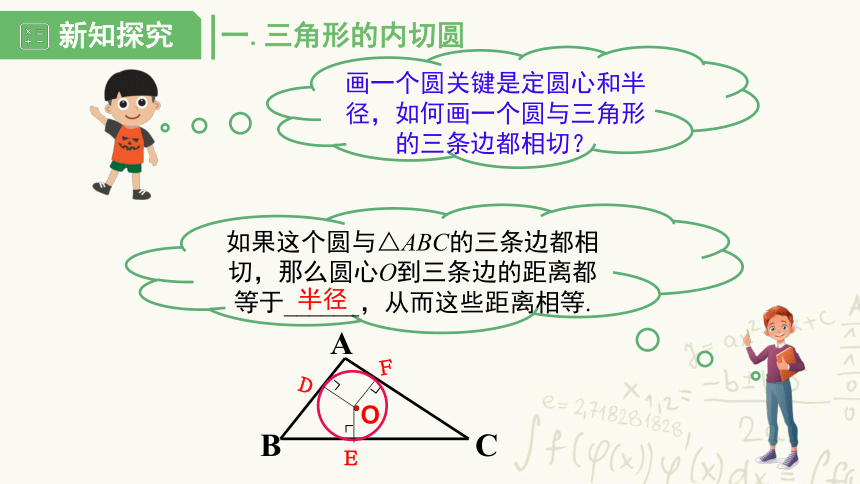
画一个圆关键是定圆心和半径,如何画一个圆与三角形的三条边都相切?
如果这个圆与△ABC的三条边都相切,那么圆心O到三条边的距离都等于______,从而这些距离相等.
A
B
C
E
∟
∟
∟
O
D
F
半径
一.三角形的内切圆
新知探究
一.三角形的内切圆
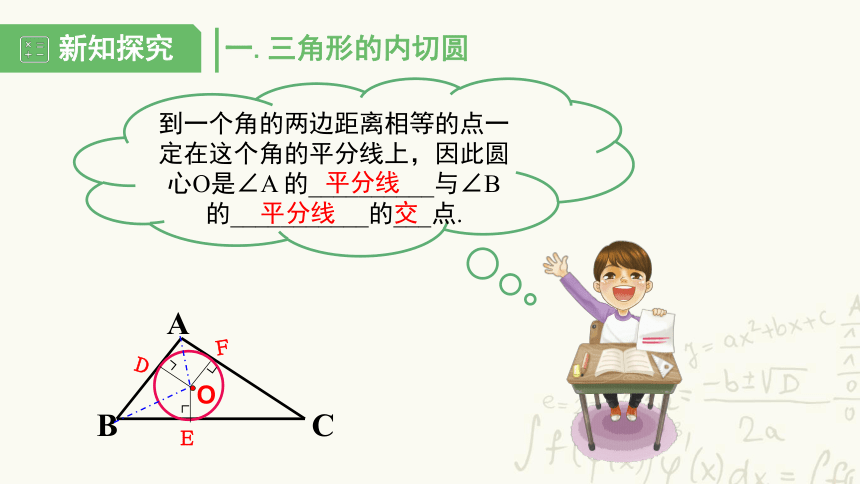
到一个角的两边距离相等的点一定在这个角的平分线上,因此圆心O是∠A
的__________与∠B的___________的___点.
A
B
C
E
∟
∟
∟
O
D
F
平分线
平分线
交
新知探究
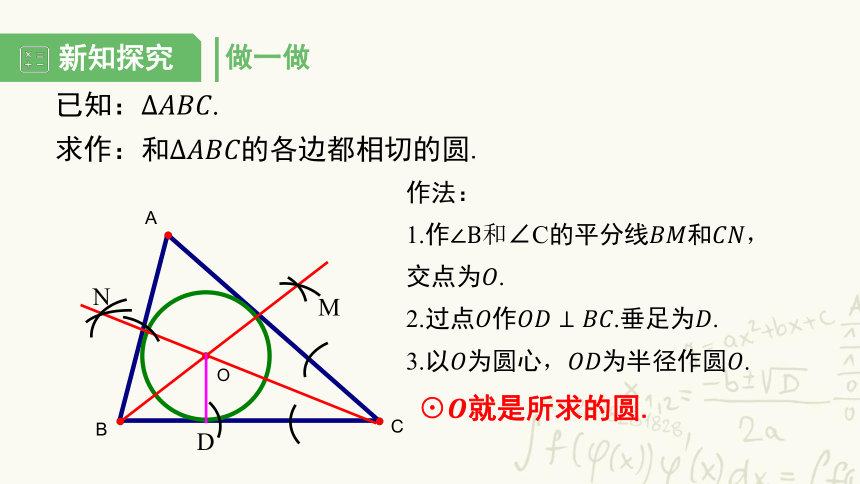
做一做
已知:.
求作:和的各边都相切的圆.
作法:
1.作和∠C的平分线和,交点为.
2.过点作.垂足为.
3.以为圆心,为半径作圆.
☉就是所求的圆.
M
N
D
新知探究
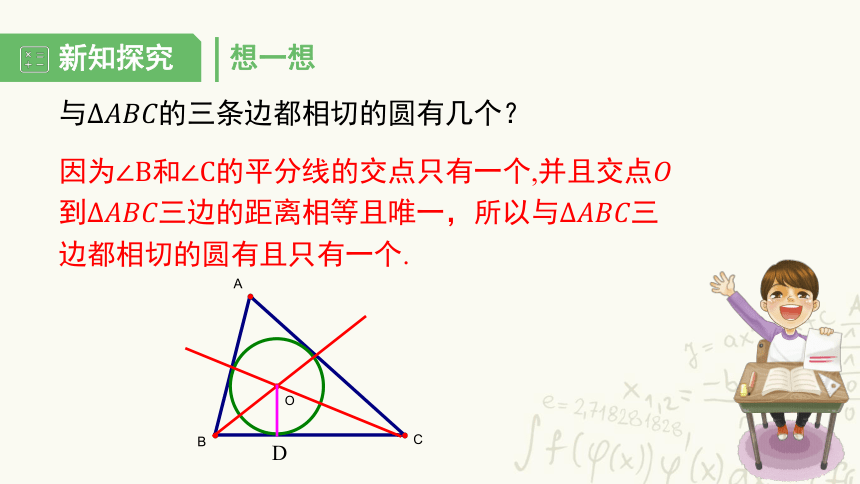
想一想
与的三条边都相切的圆有几个?
因为和的平分线的交点只有一个,并且交点到三边的距离相等且唯一,所以与三边都相切的圆有且只有一个.
D
新知探究
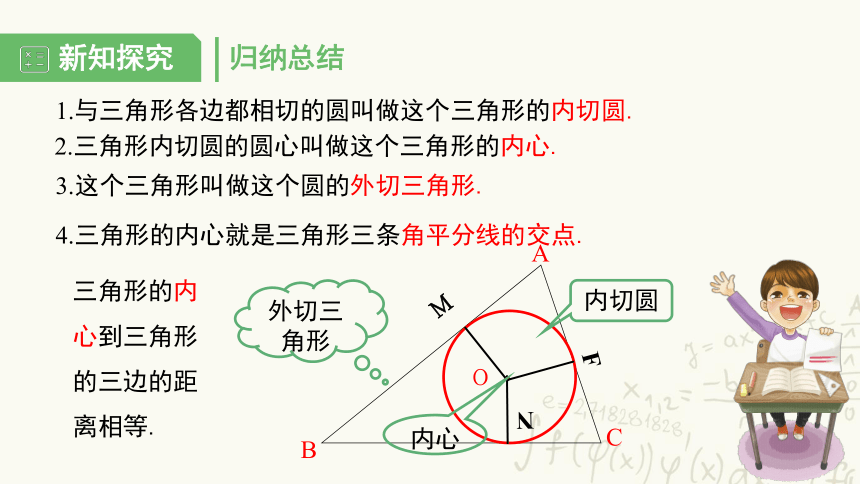
归纳总结
A
B
O
M
N
F
外切三角形
内切圆
内心
1.与三角形各边都相切的圆叫做这个三角形的内切圆.
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
4.三角形的内心就是三角形三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
C
新知探究
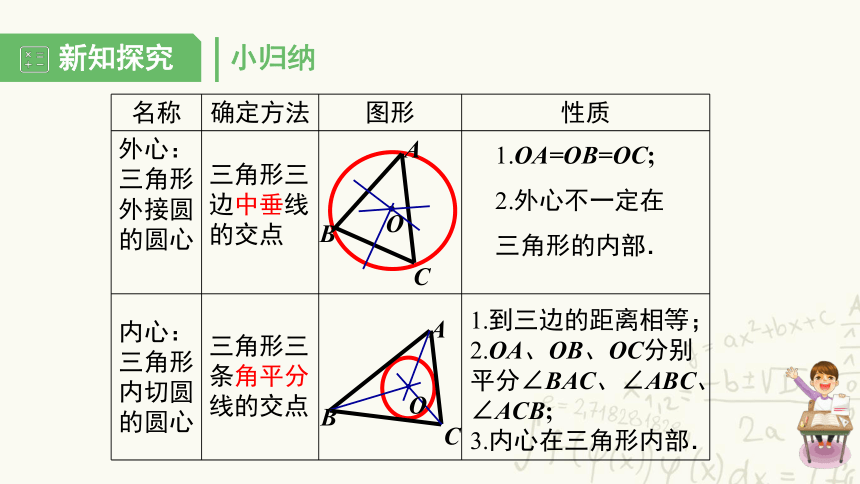
小归纳
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边中垂线的交点
1.OA=OB=OC;
2.外心不一定在三角形的内部.
三角形三条角平分线的交点
1.到三边的距离相等;
2.OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB;
3.内心在三角形内部.
A
B
O
A
B
C
O
C
新知探究
练一练
如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于E,F,则(
)
F
E
O
C
B
A
A.EF>AE+BF
B.EFC.EF=AE+BF
D.EF与AE+BF的大小关系不确定
C
新知探究
练一练
思路导引:
连接OA,OB,由O是△ABC的内心可得AO平分______,
BO平分_______.
F
E
O
C
B
A
注意:
在三角形中已知内心时常连接内心和三角形的顶点,得到角平分线.
∠CAB
∠ABC
新知探究
二.特殊三角形的内切圆半径
O
F
B
E
C
D
A
已知Rt△ABC的内切圆与三条边分别切于点D,E,F,若AC=3cm,BC=4cm,求内切圆的半径.
思路导引:
1.由勾股定理可得AB=_____cm;
2.连接OD,OE,OF,则四边形DCEO为_____形.
5
正方
r=1
新知探究
二.特殊三角形的内切圆半径
O
F
B
E
C
D
A
解:
由勾股定理得,
AB==5cm.
如图,连接OD,OE,OF.
∵
⊙O是△ABC的内切圆,
∴AD=AF,BE=BF,CD=CE,
∵OD=OE,
∠C=∠ODC=∠OEC=90°,
∴四边形DCEO是正方形,
∴OD=OE=DC=CE.
设⊙O的半径是r
cm,
则AC-r+BC-r=5,
解得r=1,
∴内切圆的半径为1cm.
新知探究
归纳总结
(1)设的直角边为,斜边为,则的内切圆的半径
或;
(2)等边三角形的内切圆半径、外接圆半径、高之比为1:2:3.
03
典型例题
典型例题
1.已知一个三角形的三边长分别为5,7,8,则其内切圆的
半径为(
)
A.
B.
C.
D.
C
2.下列语句正确的个数是(
)
过平面上三点可以作一个圆;
平分弦的直径垂直于弦;
在同圆或等圆中,相等的弦所对的圆周角相等;
三角形的内心到三角形各边的距离相等.
A.1个
B.2个
C.3个
D.4个
典型例题
A
解析:
过平面上(不在同一直线上的)三点可以作一个圆;
平分弦(不是直径)的直径垂直于弦;
在同圆或等圆中,相等的弦所对的圆周角相等;错误
三角形的内心到三角形各边的距离相等.正确
A.1个
B.2个
C.3个
D.4个
典型例题
典型例题
3.如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为(
)
A.4.5
B.4
C.3
D.2
B
I
C
B
A
典型例题
4.△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为
(1)求BF+CE的长;
(2)求△ABC的周长.
B
O
D
C
E
F
A
解:
(1)∵
△ABC外切于⊙O,切点分别为点D,E,F,
∴BF=BD,CE=CD,
∴BF+CE=BD+CD=BC=7.
BF+CE=7
△ABC的周长是20.
典型例题
B
O
D
C
E
F
A
解:
(2)如图,连接OE,OF,OA,
∵
△ABC外切于⊙O,切点分别为点D,E,F,
∴∠OEA=90°,
∠OAE=∠BAC=30°,
∴OA=2OE=2.
由勾股定理得
AE=AF===3,
∴△ABC的周长是
AB+BC+AC=AF+AE+CE+BF+BC
=3+3+7+7=20,
∴△ABC的周长是20.
04
拓展提高
拓展提高
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.
C
B
A
I
D
E
DE=2
拓展提高
解:
(1)如图,连接IB.
点I是△ABC的内心,
∠BAD=∠CAD,∠ABI=∠IBD,
又∠BIE=∠BAD+∠ABI=∠CAD+∠IBD
=∠DBE+∠IBD=∠IBE,
IE=BE.
C
B
A
I
D
E
拓展提高
(2)
在△BED和△AEB中,
∠EBD=∠CAD=∠DAB,
∠BED=∠AEB,
△BED∽△AEB
=,
BE=IE=4,AE=8,
DE==2.
C
B
A
I
D
E
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
三角形的内切圆
教学课件
湘教版九年级下册
01
新课导入
新课导入
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?下面有四种方案,请选择最佳方案.
A
B
C
A
B
C
A
B
C
A
B
C
方案一
方案二
方案三
方案四
√
新课导入
同学们知道这是为什么吗?今天就让我们一起来探究一下!
02
新知探究
新知探究
一.三角形的内切圆
猜想:方案二中的这个圆应当与三角形的三条边都相________.
A
B
C
方案二
切
∟
∟
∟
O
新知探究
画一个圆关键是定圆心和半径,如何画一个圆与三角形的三条边都相切?
如果这个圆与△ABC的三条边都相切,那么圆心O到三条边的距离都等于______,从而这些距离相等.
A
B
C
E
∟
∟
∟
O
D
F
半径
一.三角形的内切圆
新知探究
一.三角形的内切圆
到一个角的两边距离相等的点一定在这个角的平分线上,因此圆心O是∠A
的__________与∠B的___________的___点.
A
B
C
E
∟
∟
∟
O
D
F
平分线
平分线
交
新知探究
做一做
已知:.
求作:和的各边都相切的圆.
作法:
1.作和∠C的平分线和,交点为.
2.过点作.垂足为.
3.以为圆心,为半径作圆.
☉就是所求的圆.
M
N
D
新知探究
想一想
与的三条边都相切的圆有几个?
因为和的平分线的交点只有一个,并且交点到三边的距离相等且唯一,所以与三边都相切的圆有且只有一个.
D
新知探究
归纳总结
A
B
O
M
N
F
外切三角形
内切圆
内心
1.与三角形各边都相切的圆叫做这个三角形的内切圆.
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
4.三角形的内心就是三角形三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
C
新知探究
小归纳
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边中垂线的交点
1.OA=OB=OC;
2.外心不一定在三角形的内部.
三角形三条角平分线的交点
1.到三边的距离相等;
2.OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB;
3.内心在三角形内部.
A
B
O
A
B
C
O
C
新知探究
练一练
如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于E,F,则(
)
F
E
O
C
B
A
A.EF>AE+BF
B.EF
D.EF与AE+BF的大小关系不确定
C
新知探究
练一练
思路导引:
连接OA,OB,由O是△ABC的内心可得AO平分______,
BO平分_______.
F
E
O
C
B
A
注意:
在三角形中已知内心时常连接内心和三角形的顶点,得到角平分线.
∠CAB
∠ABC
新知探究
二.特殊三角形的内切圆半径
O
F
B
E
C
D
A
已知Rt△ABC的内切圆与三条边分别切于点D,E,F,若AC=3cm,BC=4cm,求内切圆的半径.
思路导引:
1.由勾股定理可得AB=_____cm;
2.连接OD,OE,OF,则四边形DCEO为_____形.
5
正方
r=1
新知探究
二.特殊三角形的内切圆半径
O
F
B
E
C
D
A
解:
由勾股定理得,
AB==5cm.
如图,连接OD,OE,OF.
∵
⊙O是△ABC的内切圆,
∴AD=AF,BE=BF,CD=CE,
∵OD=OE,
∠C=∠ODC=∠OEC=90°,
∴四边形DCEO是正方形,
∴OD=OE=DC=CE.
设⊙O的半径是r
cm,
则AC-r+BC-r=5,
解得r=1,
∴内切圆的半径为1cm.
新知探究
归纳总结
(1)设的直角边为,斜边为,则的内切圆的半径
或;
(2)等边三角形的内切圆半径、外接圆半径、高之比为1:2:3.
03
典型例题
典型例题
1.已知一个三角形的三边长分别为5,7,8,则其内切圆的
半径为(
)
A.
B.
C.
D.
C
2.下列语句正确的个数是(
)
过平面上三点可以作一个圆;
平分弦的直径垂直于弦;
在同圆或等圆中,相等的弦所对的圆周角相等;
三角形的内心到三角形各边的距离相等.
A.1个
B.2个
C.3个
D.4个
典型例题
A
解析:
过平面上(不在同一直线上的)三点可以作一个圆;
平分弦(不是直径)的直径垂直于弦;
在同圆或等圆中,相等的弦所对的圆周角相等;错误
三角形的内心到三角形各边的距离相等.正确
A.1个
B.2个
C.3个
D.4个
典型例题
典型例题
3.如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为(
)
A.4.5
B.4
C.3
D.2
B
I
C
B
A
典型例题
4.△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为
(1)求BF+CE的长;
(2)求△ABC的周长.
B
O
D
C
E
F
A
解:
(1)∵
△ABC外切于⊙O,切点分别为点D,E,F,
∴BF=BD,CE=CD,
∴BF+CE=BD+CD=BC=7.
BF+CE=7
△ABC的周长是20.
典型例题
B
O
D
C
E
F
A
解:
(2)如图,连接OE,OF,OA,
∵
△ABC外切于⊙O,切点分别为点D,E,F,
∴∠OEA=90°,
∠OAE=∠BAC=30°,
∴OA=2OE=2.
由勾股定理得
AE=AF===3,
∴△ABC的周长是
AB+BC+AC=AF+AE+CE+BF+BC
=3+3+7+7=20,
∴△ABC的周长是20.
04
拓展提高
拓展提高
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.
C
B
A
I
D
E
DE=2
拓展提高
解:
(1)如图,连接IB.
点I是△ABC的内心,
∠BAD=∠CAD,∠ABI=∠IBD,
又∠BIE=∠BAD+∠ABI=∠CAD+∠IBD
=∠DBE+∠IBD=∠IBE,
IE=BE.
C
B
A
I
D
E
拓展提高
(2)
在△BED和△AEB中,
∠EBD=∠CAD=∠DAB,
∠BED=∠AEB,
△BED∽△AEB
=,
BE=IE=4,AE=8,
DE==2.
C
B
A
I
D
E
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
