湘教版数学九年级下册2.5.3 切线长定理教学课件(共29张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.3 切线长定理教学课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
切线长定理
教学课件
湘教版九年级下册
01
新课导入
新课导入
P
O
O.
P
B
A
A
B
问题1
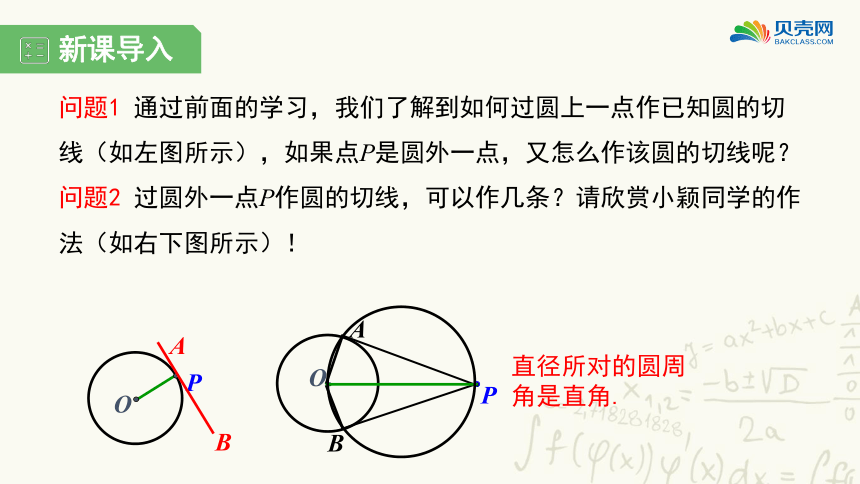
通过前面的学习,我们了解到如何过圆上一点作已知圆的切线(如左图所示),如果点P是圆外一点,又怎么作该圆的切线呢?
问题2
过圆外一点P作圆的切线,可以作几条?请欣赏小颖同学的作法(如右下图所示)!
直径所对的圆周角是直角.
02
新知探究
新知探究
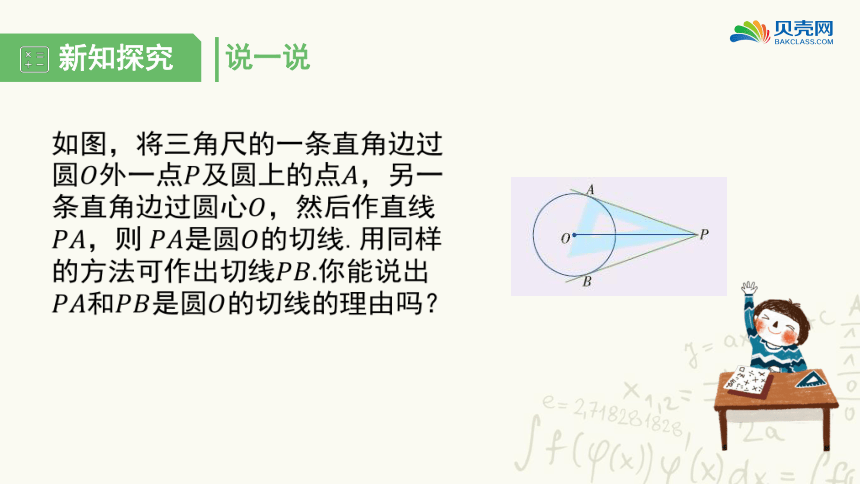
如图,将三角尺的一条直角边过圆外一点及圆上的点,另一条直角边过圆心,然后作直线,则是圆的切线.用同样的方法可作出切线你能说出和是圆的切线的理由吗?
说一说
新知探究
一.切线长的定义
P
1.切线长的定义:
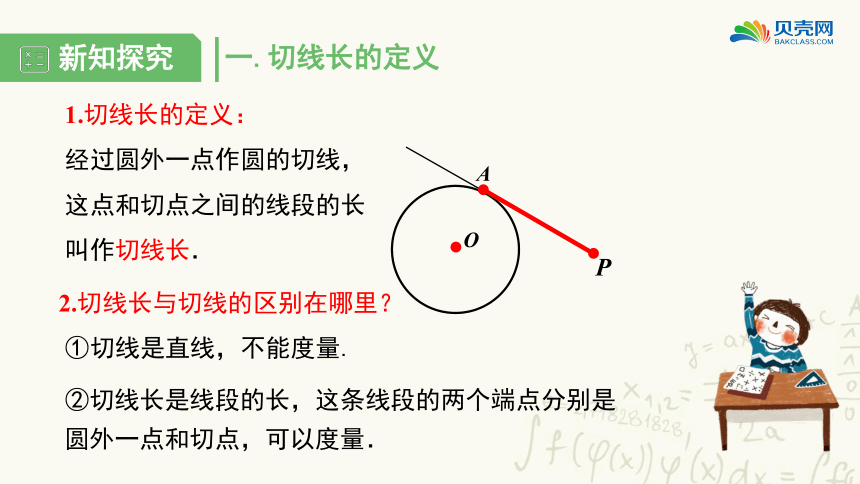
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
新知探究
B
P
O
A
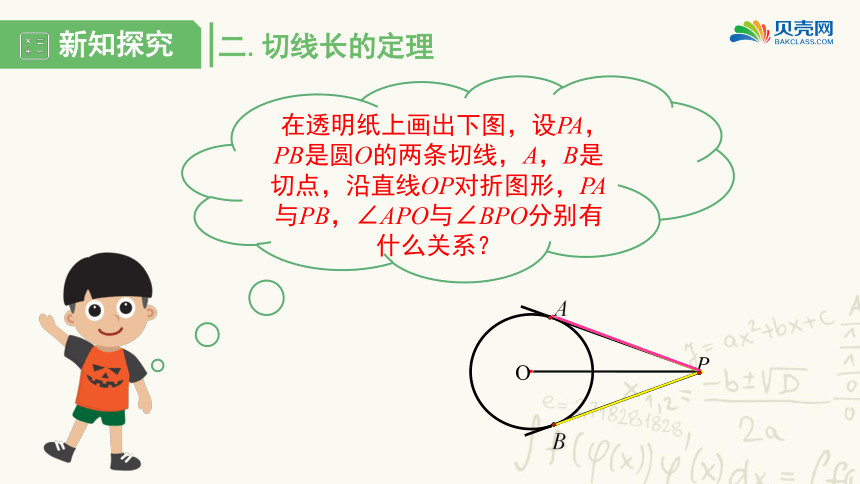
在透明纸上画出下图,设PA,PB是圆O的两条切线,A,B是切点,沿直线OP对折图形,PA与PB,∠APO与∠BPO分别有什么关系?
二.切线长的定理
新知探究
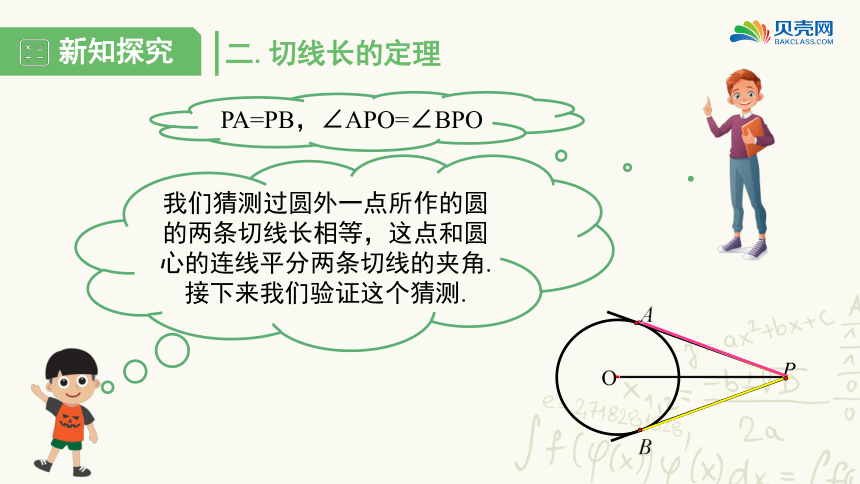
PA=PB,∠APO=∠BPO
B
P
O
A
我们猜测过圆外一点所作的圆的两条切线长相等,这点和圆心的连线平分两条切线的夹角.接下来我们验证这个猜测.
二.切线长的定理
新知探究
推论证明
B
P
O
A
如图,连接,
圆相切,点,是切点,
,即
,
,
新知探究
归纳总结
切线长定理:
过圆外一点引所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
、分别切☉于、
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
B
P
O
A
新知探究
练一练
如图,⊙与△ABC中AB,AC的延长线及BC边分别相切于F,D,E三点,且∠ACB=90°,∠A,∠ABC,∠ACB所对的边长依次为3,4,5,则⊙的半径是________.
O
F
E
D
C
B
A
思路导引:
1.由切线长定理可得AF=________,
BE=________,CE=______________.
2.要求⊙的半径,可连接___,___.
2
AD
BF
CD
OE
OD
新知探究
归纳总结
当已知条件中有多条切线时,要考虑应用切线长定理,常作的辅助线是作过切点的半径.
新知探究
三.切线长定理的应用
如图,四边形ABCD是圆O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为__________.
O
D
C
B
A
44
新知探究
归纳总结
切线长问题辅助线添加方法
连接圆心和圆外一点.
连接两切点;
分别连接圆心和切点;
03
典型例题
典型例题
1.如图,P为圆O外一点,PA,PB分别切圆O于点A,B,CD切圆O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长为(
)
O
B
A
C
E
D
P
A.5
B.7
C.8
D.10
D
典型例题
2.如图,PA切圆O于点A,PB切圆O于点B,OP交圆O于点C.下列结论中,错误的是(
)
D
O
C
P
2
1
A
B
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.PA2=PC·PO
典型例题
3.如图,PA,PB,CD是圆O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=40°,PA=5,有下列结论:①PB=5;
②△PCD的周长为5;③∠COD=70°.正确结论的个数为(
)
B
O
B
A
C
E
D
P
A.3
B.2
C.1
D.0
典型例题
4.如图,PA,PB是圆O的切线,A,B为切点,AC是圆O的直径,∠P=60°.
(1)求∠BAC的度数.
(2)当OA=2时,求AB的长.
A
P
O
B
C
30°
AB=2
典型例题
解:
(1)
PA,PB是圆O的切线,
AP=BP,
∠P=60°,
∠PAB=60°,
PA是圆O的切线,
∠PAC=90°,
∠BAC=90°-60°=30°.
A
P
O
B
C
典型例题
解:
(2)如图,连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
P=4,
由勾股定理得AP=2,
AP=BP,∠APB=60°,
△APB是等角三角形,
AB=AP=2.
A
P
O
B
C
04
拓展提高
拓展提高
如图,已知射线PO与圆O交于A,B两点,PC,PD分别切圆O于点C,D.若CD=12,tan∠CPO=,求PO的长.
O
C
A
B
D
P
解:
如图,连接OC.
PC,PD分别切圆O于点C,D,
PC=PD,
∠CPO=∠DPO,
CD⊥AB.
OP=15
E
拓展提高
CD=12,
DE=CE=CD=6,
tan∠CPO=,
在Rt△EPC中,PE=12.
由勾股定理得CP=6,
PC切圆O于点C,
∠OCP=90°.
在Rt△OPC中,
tan∠CPO=,
=,
OC=3,
OP==15.
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
切线长定理
教学课件
湘教版九年级下册
01
新课导入
新课导入
P
O
O.
P
B
A
A
B
问题1
通过前面的学习,我们了解到如何过圆上一点作已知圆的切线(如左图所示),如果点P是圆外一点,又怎么作该圆的切线呢?
问题2
过圆外一点P作圆的切线,可以作几条?请欣赏小颖同学的作法(如右下图所示)!
直径所对的圆周角是直角.
02
新知探究
新知探究
如图,将三角尺的一条直角边过圆外一点及圆上的点,另一条直角边过圆心,然后作直线,则是圆的切线.用同样的方法可作出切线你能说出和是圆的切线的理由吗?
说一说
新知探究
一.切线长的定义
P
1.切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
新知探究
B
P
O
A
在透明纸上画出下图,设PA,PB是圆O的两条切线,A,B是切点,沿直线OP对折图形,PA与PB,∠APO与∠BPO分别有什么关系?
二.切线长的定理
新知探究
PA=PB,∠APO=∠BPO
B
P
O
A
我们猜测过圆外一点所作的圆的两条切线长相等,这点和圆心的连线平分两条切线的夹角.接下来我们验证这个猜测.
二.切线长的定理
新知探究
推论证明
B
P
O
A
如图,连接,
圆相切,点,是切点,
,即
,
,
新知探究
归纳总结
切线长定理:
过圆外一点引所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
、分别切☉于、
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
B
P
O
A
新知探究
练一练
如图,⊙与△ABC中AB,AC的延长线及BC边分别相切于F,D,E三点,且∠ACB=90°,∠A,∠ABC,∠ACB所对的边长依次为3,4,5,则⊙的半径是________.
O
F
E
D
C
B
A
思路导引:
1.由切线长定理可得AF=________,
BE=________,CE=______________.
2.要求⊙的半径,可连接___,___.
2
AD
BF
CD
OE
OD
新知探究
归纳总结
当已知条件中有多条切线时,要考虑应用切线长定理,常作的辅助线是作过切点的半径.
新知探究
三.切线长定理的应用
如图,四边形ABCD是圆O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为__________.
O
D
C
B
A
44
新知探究
归纳总结
切线长问题辅助线添加方法
连接圆心和圆外一点.
连接两切点;
分别连接圆心和切点;
03
典型例题
典型例题
1.如图,P为圆O外一点,PA,PB分别切圆O于点A,B,CD切圆O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长为(
)
O
B
A
C
E
D
P
A.5
B.7
C.8
D.10
D
典型例题
2.如图,PA切圆O于点A,PB切圆O于点B,OP交圆O于点C.下列结论中,错误的是(
)
D
O
C
P
2
1
A
B
A.∠1=∠2
B.PA=PB
C.AB⊥OP
D.PA2=PC·PO
典型例题
3.如图,PA,PB,CD是圆O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=40°,PA=5,有下列结论:①PB=5;
②△PCD的周长为5;③∠COD=70°.正确结论的个数为(
)
B
O
B
A
C
E
D
P
A.3
B.2
C.1
D.0
典型例题
4.如图,PA,PB是圆O的切线,A,B为切点,AC是圆O的直径,∠P=60°.
(1)求∠BAC的度数.
(2)当OA=2时,求AB的长.
A
P
O
B
C
30°
AB=2
典型例题
解:
(1)
PA,PB是圆O的切线,
AP=BP,
∠P=60°,
∠PAB=60°,
PA是圆O的切线,
∠PAC=90°,
∠BAC=90°-60°=30°.
A
P
O
B
C
典型例题
解:
(2)如图,连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
P=4,
由勾股定理得AP=2,
AP=BP,∠APB=60°,
△APB是等角三角形,
AB=AP=2.
A
P
O
B
C
04
拓展提高
拓展提高
如图,已知射线PO与圆O交于A,B两点,PC,PD分别切圆O于点C,D.若CD=12,tan∠CPO=,求PO的长.
O
C
A
B
D
P
解:
如图,连接OC.
PC,PD分别切圆O于点C,D,
PC=PD,
∠CPO=∠DPO,
CD⊥AB.
OP=15
E
拓展提高
CD=12,
DE=CE=CD=6,
tan∠CPO=,
在Rt△EPC中,PE=12.
由勾股定理得CP=6,
PC切圆O于点C,
∠OCP=90°.
在Rt△OPC中,
tan∠CPO=,
=,
OC=3,
OP==15.
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
