湘教版数学九年级下册2.5.1 直线与圆的位置关系教学课件(共28张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.5.1 直线与圆的位置关系教学课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 23:42:36 | ||
图片预览







文档简介
(共28张PPT)
直线与圆的位置关系
教学课件
湘教版九年级下册
01
新课导入
新课导入
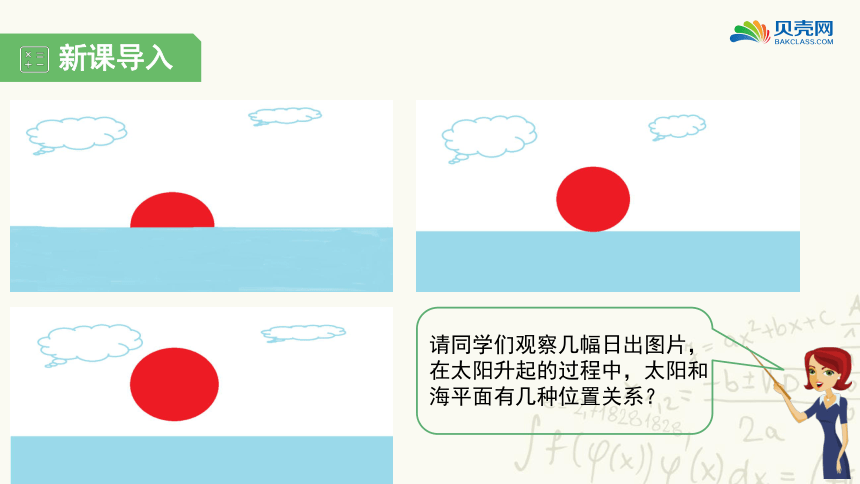
请同学们观察几幅日出图片,在太阳升起的过程中,太阳和海平面有几种位置关系?
新课导入
在学习新知识之前,同学们还记得点与圆的位置关系吗?如果设圆的半径为r,点到圆心的距离为d,大家能用d与r之间的距离来表示点与圆的位置关系吗?
新课导入
点和圆的位置关系有几种?
dd=r
d>r
用数量关系如何来
判断呢?
⑴点在圆内
P
·
⑵点在圆上
⑶点在圆外
·
P
(令OP=d
)
·
P
02
新知探究
新知探究
请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
●
●
●
l
0
2
确定直线与圆的位置关系
新知探究
根据上面观察的发现结果,你认为直线与圆的位置关系可以分为几类?你分类的依据是什么?分别把它们的图形在草稿纸上画出来.
想一想
新知探究
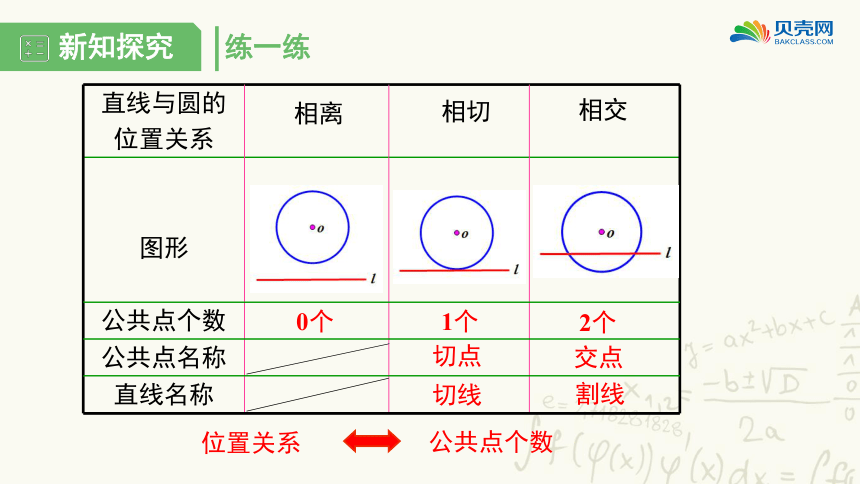
练一练
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
新知探究
练一练
已知⊙O的半径为5cm,圆心O到直线L的距离为5cm,则直线L与⊙O的位置关系为(
)
A.相交
B.相切
C.相离
D.无法确定
B
新知探究
用数量关系判断直线与圆的位置关系
刚才同学们用硬币移近直线的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
圆心到直线的距离
在发生变化;
首先距离大于半径,
而后距离等于半径,
最后距离小于半径.
新知探究
二次函数的自变量的取值范围
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
新知探究
归纳总结
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
公共点个数
直线与圆的位置关系
的性质与判定的区别:
位置关系数量关系.
新知探究
练一练
(3)若AB和⊙O相交,
则
.
已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据条件,填写d的范围:
(1)若AB和⊙O相离,
则
;
(2)若AB和⊙O相切,
则
;
d
>
5cm
d
=
5cm
0cm≤d
<
5cm
03
典型例题
典型例题
1.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆,
(1)当r满足________________时,⊙C与直线AB相离.
(2)当r满足________________时,⊙C与直线AB相切.
(3)当r满足________________时,⊙C与直线AB相交.
B
C
A
4
5
3
0r=2.4
r>2.4
典型例题
2.已知⊙O的半径为5,且圆心O到直线L的距离d=+|-2|,则直线L与圆的位置关系是(
)
A.相交
B.相切
C.相离
D.无法确定
C
典型例题
3.如图,在中,,,,若分别是的中点,则以为直径的圆与的位置关系是(
)
A.相交
B.相切
C.相离
D.无法确定
A
典型例题
解析:过点作于点,交于点,
,,
分别是的中点,
,
,
,
,
,
以为直径的圆与的位置关系是:相交.
04
拓展提高
拓展提高
如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB有怎样的位置关系?
(2)当OC等于多少时,⊙O与直线AB相切?
A
B
C
相离
OC=0.5
拓展提高
解:
(1)作CM,垂足为M,如图所示.
在Rt△ABC中,
,
AC
BC=AB
CM,
CM=.
>2,
此时⊙O与直线AB相离.
A
B
C
M
O
拓展提高
解:
(2)作ON,垂足为N,如图所示.
∥CM
,
△AON
∽△ACM,
=.
设OC=x,则AO=3-x,
,
x=0.5,
当OC=0.5时,⊙O与直线AB相切.
A
B
C
M
O
N
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
直线与圆的位置关系
教学课件
湘教版九年级下册
01
新课导入
新课导入
请同学们观察几幅日出图片,在太阳升起的过程中,太阳和海平面有几种位置关系?
新课导入
在学习新知识之前,同学们还记得点与圆的位置关系吗?如果设圆的半径为r,点到圆心的距离为d,大家能用d与r之间的距离来表示点与圆的位置关系吗?
新课导入
点和圆的位置关系有几种?
d
d>r
用数量关系如何来
判断呢?
⑴点在圆内
P
·
⑵点在圆上
⑶点在圆外
·
P
(令OP=d
)
·
P
02
新知探究
新知探究
请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
●
●
●
l
0
2
确定直线与圆的位置关系
新知探究
根据上面观察的发现结果,你认为直线与圆的位置关系可以分为几类?你分类的依据是什么?分别把它们的图形在草稿纸上画出来.
想一想
新知探究
练一练
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
新知探究
练一练
已知⊙O的半径为5cm,圆心O到直线L的距离为5cm,则直线L与⊙O的位置关系为(
)
A.相交
B.相切
C.相离
D.无法确定
B
新知探究
用数量关系判断直线与圆的位置关系
刚才同学们用硬币移近直线的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
圆心到直线的距离
在发生变化;
首先距离大于半径,
而后距离等于半径,
最后距离小于半径.
新知探究
二次函数的自变量的取值范围
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
新知探究
归纳总结
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
公共点个数
直线与圆的位置关系
的性质与判定的区别:
位置关系数量关系.
新知探究
练一练
(3)若AB和⊙O相交,
则
.
已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据条件,填写d的范围:
(1)若AB和⊙O相离,
则
;
(2)若AB和⊙O相切,
则
;
d
>
5cm
d
=
5cm
0cm≤d
<
5cm
03
典型例题
典型例题
1.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆,
(1)当r满足________________时,⊙C与直线AB相离.
(2)当r满足________________时,⊙C与直线AB相切.
(3)当r满足________________时,⊙C与直线AB相交.
B
C
A
4
5
3
0
r>2.4
典型例题
2.已知⊙O的半径为5,且圆心O到直线L的距离d=+|-2|,则直线L与圆的位置关系是(
)
A.相交
B.相切
C.相离
D.无法确定
C
典型例题
3.如图,在中,,,,若分别是的中点,则以为直径的圆与的位置关系是(
)
A.相交
B.相切
C.相离
D.无法确定
A
典型例题
解析:过点作于点,交于点,
,,
分别是的中点,
,
,
,
,
,
以为直径的圆与的位置关系是:相交.
04
拓展提高
拓展提高
如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB有怎样的位置关系?
(2)当OC等于多少时,⊙O与直线AB相切?
A
B
C
相离
OC=0.5
拓展提高
解:
(1)作CM,垂足为M,如图所示.
在Rt△ABC中,
,
AC
BC=AB
CM,
CM=.
>2,
此时⊙O与直线AB相离.
A
B
C
M
O
拓展提高
解:
(2)作ON,垂足为N,如图所示.
∥CM
,
△AON
∽△ACM,
=.
设OC=x,则AO=3-x,
,
x=0.5,
当OC=0.5时,⊙O与直线AB相切.
A
B
C
M
O
N
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
