湘教版数学九年级下册2.3 垂径定理教学课件(共34张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.3 垂径定理教学课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
垂径定理
教学课件
湘教版九年级下册
01
新课导入
新课导入
初升的太阳真美呀!你知道太阳从目前所处的位置到恰好跳出海平面需要多长时间吗?学习完今天的知识,这个问题就可以解决了!
02
新知探究
新知探究
一.垂径定理及其推论
如图,AB是⊙O的一条弦,
直径CD⊥AB,
垂足为P.你能发现图中有那些相等的线段和弧?
为什么?
·
O
A
B
D
P
C
线段:
AP=BP
弧:
AC=BC,
AD=BD
⌒
⌒
⌒
⌒
新知探究
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AP与BP重合,AC和BC,AD与BD重合.
⌒
⌒
⌒
⌒
·
O
A
B
D
P
C
新知探究
归纳总结
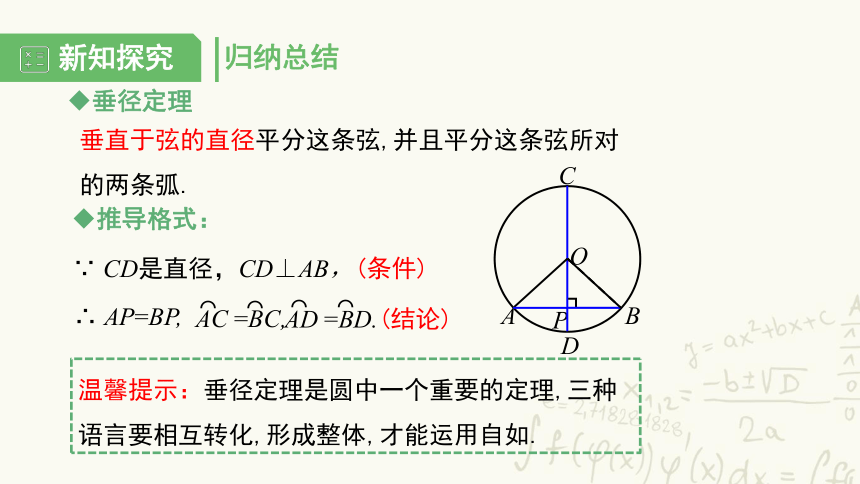
垂径定理
·
O
A
B
C
D
P
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
∵
CD是直径,CD⊥AB,(条件)
∴
AP=BP,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.(结论)
推导格式:
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
新知探究
练一练
·
O
A
B
D
C
E
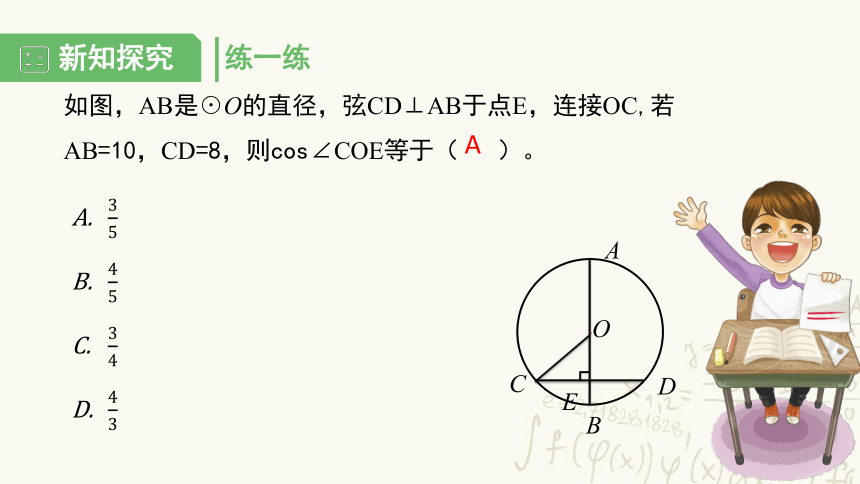
如图,AB是☉O的直径,弦CD⊥AB于点E,连接OC,若AB=10,CD=8,则cos∠COE等于(
)。
A
新知探究
想一想
下列图形是否具备垂径定理的条件?
O
E
D
C
A
B
是
不是
是
不是
新知探究
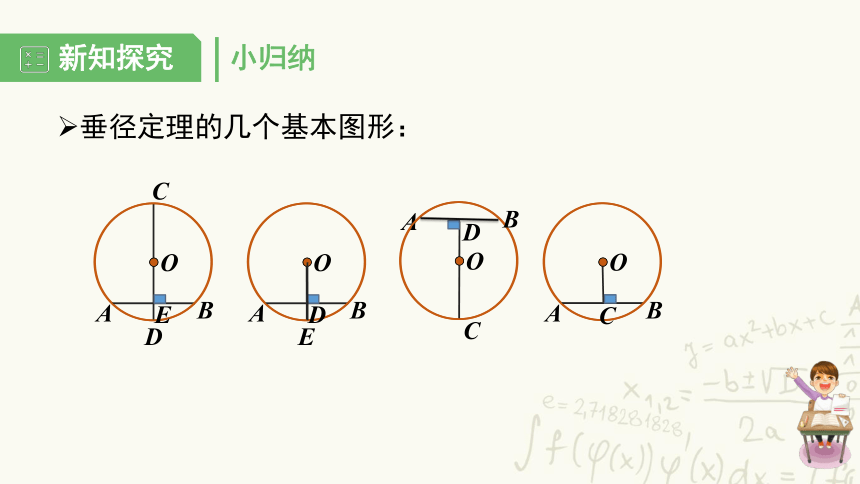
小归纳
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
新知探究
练一练
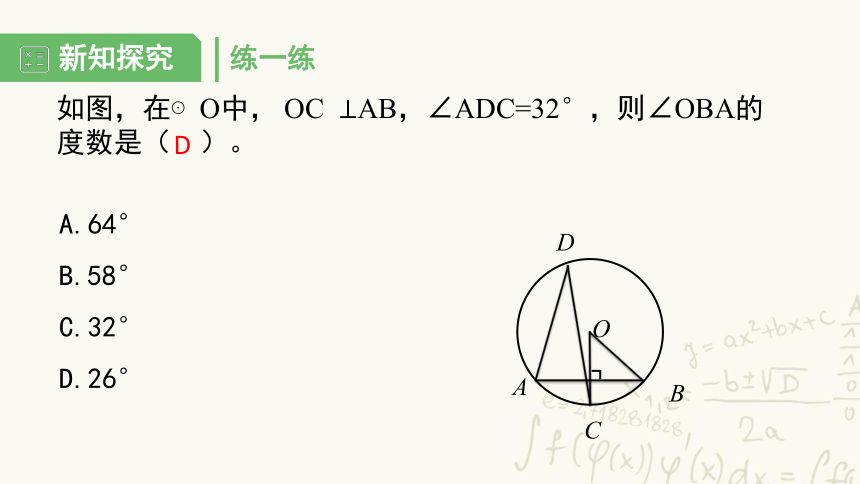
如图,在⊙O中,
OCAB,∠ADC=32°,则∠OBA的度数是(
)。
D
O
A
B
D
C
·
A.64°
B.58°
C.32°
D.26°
新知探究
归纳总结
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于这条弦,并且平分这条
弦所对的两条弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
新知探究
归纳总结
垂径定理的本质是:
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
新知探究
二.垂径定理的实际应用
问题:“图上”太阳与海平线交于A、B两点,“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,则“图上”太阳升起的速度为多少?现在运用一下垂径定理来解决一下吧!
A
B
新知探究
解答
A
B
O
C
D
解:如图,用AB表示海平面,设AB所在圆的圆心为O。
作与弦AB垂直的直径,交AB于点C,交圆O于点D,连接OB.?根据垂径定理可知BC=AB=4(厘米)
∴在Rt△OBC中,
OC===3(厘米)
·
海平面
∴DC=OD+OC=8(厘米)
∴“图上”太阳升起的速度为8÷16=0.5(厘米/分)
新知探究
归纳总结
在圆中有关弦长a,半径r,
弦心距d(圆心到弦的距离),弓形高h的计算题,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
新知探究
练一练
把球放在长方体纸盒内,球的一部分露在盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为_______cm.
F
D
C
B
A
E
思路导引:
1.竖直平面内,圆心一定在EF的___________线上。
2.先确定圆的_________,在找到_______求出半径。
10
垂直平分
一条直径
圆心
新知探究
归纳总结
把实际问题转化为在圆中解决有关弦、半径的求值问题,常常需要作垂直于弦的直径作为辅助线,这样就把垂直定理和勾股定理结合起来,容易得到圆的半径r,圆心到弦的距离d和弦长a之间的关系:r2=d2+()2.已知其中两个,可求出第三个。
03
典型例题
典型例题
1.如图,
在⊙O中,直径CD⊥弦AB
,则下列结论正确的是(
)。
B
O
A
B
D
C
·
A.AC=AB
B.∠C=∠BOD
C.∠C=∠B
D.∠A=∠BOD
典型例题
2.如图,在⊙中,AB是直径,CD是弦,
CD
⊥AB,垂足为E,连接CO,AD,
∠BAD=20°,则下列说法正确的是(
)。
O
A
B
D
C
·
E
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
D
典型例题
3.如图,AB是⊙的直径,且经过弦CD的中点H,已知cos∠COB=,BD=5,则OH的长为(
)。
A
B
D
C
·
H
O
1
D
典型例题
4.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且点O到直线AB的距离为6,求AC的长。
O
.
A
C
D
B
AC=8-
典型例题
解:
(1)证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
∴
AE-CE=BE-DE
即
AC=BD.
O
.
A
C
D
B
E
典型例题
O
.
A
C
D
B
(2)
由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,易知OE=6
∴CE=
==
AE=
==8
∴AC=AE-CE=8-
04
拓展提高
拓展提高
1.如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙交射线AQ于点E,F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长。
A
B
O
C
·
P
Q
F
E
4cm
6cm
拓展提高
解:
(1)如图,过点O作OHEF,
垂足为点H,则∠AHO=90°
在Rt△AHO中,
∠AHO=90°,∠PAQ=30°
∴OH=AO
BC=10cm,∴BO=5cm
AO=AB+BO,AB=3cm
∴AO=3+5=8(cm)
∴OH=4cm,即圆心O到AQ的距离为4cm.
O
C
·
P
A
B
Q
F
E
H
拓展提高
(2)连接OE.
在Rt△EOH中,
=
EO=5cm,OH=4cm,
∴EH=
==3(cm)
OH过圆心O,,
∴EF=2EH=6(cm)
A
B
O
C
·
P
Q
F
E
H
05
课堂小结
课堂小结
垂径定理
内容
推论
实际应用
一条直线满足:
①过圆心;
②垂直于弦;
③平分弦(不是直径);
④平分弦所对的优弧;
⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论
(“知二推三”)
垂直于弦的直径平分这条弦,
并且平分这条弦所对的两条弧.
06
作业布置
作业布置
谢
谢
观
看
垂径定理
教学课件
湘教版九年级下册
01
新课导入
新课导入
初升的太阳真美呀!你知道太阳从目前所处的位置到恰好跳出海平面需要多长时间吗?学习完今天的知识,这个问题就可以解决了!
02
新知探究
新知探究
一.垂径定理及其推论
如图,AB是⊙O的一条弦,
直径CD⊥AB,
垂足为P.你能发现图中有那些相等的线段和弧?
为什么?
·
O
A
B
D
P
C
线段:
AP=BP
弧:
AC=BC,
AD=BD
⌒
⌒
⌒
⌒
新知探究
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AP与BP重合,AC和BC,AD与BD重合.
⌒
⌒
⌒
⌒
·
O
A
B
D
P
C
新知探究
归纳总结
垂径定理
·
O
A
B
C
D
P
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
∵
CD是直径,CD⊥AB,(条件)
∴
AP=BP,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.(结论)
推导格式:
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
新知探究
练一练
·
O
A
B
D
C
E
如图,AB是☉O的直径,弦CD⊥AB于点E,连接OC,若AB=10,CD=8,则cos∠COE等于(
)。
A
新知探究
想一想
下列图形是否具备垂径定理的条件?
O
E
D
C
A
B
是
不是
是
不是
新知探究
小归纳
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
新知探究
练一练
如图,在⊙O中,
OCAB,∠ADC=32°,则∠OBA的度数是(
)。
D
O
A
B
D
C
·
A.64°
B.58°
C.32°
D.26°
新知探究
归纳总结
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于这条弦,并且平分这条
弦所对的两条弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
新知探究
归纳总结
垂径定理的本质是:
满足其中任两条,必定同时满足另三条
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
新知探究
二.垂径定理的实际应用
问题:“图上”太阳与海平线交于A、B两点,“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,则“图上”太阳升起的速度为多少?现在运用一下垂径定理来解决一下吧!
A
B
新知探究
解答
A
B
O
C
D
解:如图,用AB表示海平面,设AB所在圆的圆心为O。
作与弦AB垂直的直径,交AB于点C,交圆O于点D,连接OB.?根据垂径定理可知BC=AB=4(厘米)
∴在Rt△OBC中,
OC===3(厘米)
·
海平面
∴DC=OD+OC=8(厘米)
∴“图上”太阳升起的速度为8÷16=0.5(厘米/分)
新知探究
归纳总结
在圆中有关弦长a,半径r,
弦心距d(圆心到弦的距离),弓形高h的计算题,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
新知探究
练一练
把球放在长方体纸盒内,球的一部分露在盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为_______cm.
F
D
C
B
A
E
思路导引:
1.竖直平面内,圆心一定在EF的___________线上。
2.先确定圆的_________,在找到_______求出半径。
10
垂直平分
一条直径
圆心
新知探究
归纳总结
把实际问题转化为在圆中解决有关弦、半径的求值问题,常常需要作垂直于弦的直径作为辅助线,这样就把垂直定理和勾股定理结合起来,容易得到圆的半径r,圆心到弦的距离d和弦长a之间的关系:r2=d2+()2.已知其中两个,可求出第三个。
03
典型例题
典型例题
1.如图,
在⊙O中,直径CD⊥弦AB
,则下列结论正确的是(
)。
B
O
A
B
D
C
·
A.AC=AB
B.∠C=∠BOD
C.∠C=∠B
D.∠A=∠BOD
典型例题
2.如图,在⊙中,AB是直径,CD是弦,
CD
⊥AB,垂足为E,连接CO,AD,
∠BAD=20°,则下列说法正确的是(
)。
O
A
B
D
C
·
E
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
D
典型例题
3.如图,AB是⊙的直径,且经过弦CD的中点H,已知cos∠COB=,BD=5,则OH的长为(
)。
A
B
D
C
·
H
O
1
D
典型例题
4.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且点O到直线AB的距离为6,求AC的长。
O
.
A
C
D
B
AC=8-
典型例题
解:
(1)证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
∴
AE-CE=BE-DE
即
AC=BD.
O
.
A
C
D
B
E
典型例题
O
.
A
C
D
B
(2)
由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,易知OE=6
∴CE=
==
AE=
==8
∴AC=AE-CE=8-
04
拓展提高
拓展提高
1.如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙交射线AQ于点E,F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长。
A
B
O
C
·
P
Q
F
E
4cm
6cm
拓展提高
解:
(1)如图,过点O作OHEF,
垂足为点H,则∠AHO=90°
在Rt△AHO中,
∠AHO=90°,∠PAQ=30°
∴OH=AO
BC=10cm,∴BO=5cm
AO=AB+BO,AB=3cm
∴AO=3+5=8(cm)
∴OH=4cm,即圆心O到AQ的距离为4cm.
O
C
·
P
A
B
Q
F
E
H
拓展提高
(2)连接OE.
在Rt△EOH中,
=
EO=5cm,OH=4cm,
∴EH=
==3(cm)
OH过圆心O,,
∴EF=2EH=6(cm)
A
B
O
C
·
P
Q
F
E
H
05
课堂小结
课堂小结
垂径定理
内容
推论
实际应用
一条直线满足:
①过圆心;
②垂直于弦;
③平分弦(不是直径);
④平分弦所对的优弧;
⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论
(“知二推三”)
垂直于弦的直径平分这条弦,
并且平分这条弦所对的两条弧.
06
作业布置
作业布置
谢
谢
观
看
