湘教版数学九年级下册2.2 圆心角、圆周角教学课件(共34张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.2 圆心角、圆周角教学课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览





文档简介
(共34张PPT)
圆心角与圆周角
教学课件
湘教版九年级下册
01
新课导入
新课导入
在图片中存在着不同的角,同学们发现这些角有什么相同的特征码?
好像角的顶点都是在中心的。
今天,我们就让我们来学习一下这个顶点在中心的角吧!
02
新知探究
新知探究
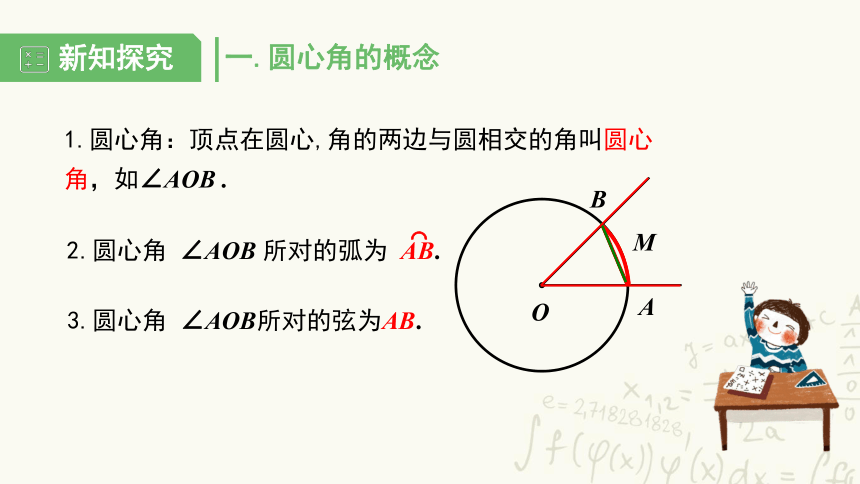
一.圆心角的概念
O
A
B
M
1.圆心角:顶点在圆心,角的两边与圆相交的角叫圆心角,如∠AOB
.
3.圆心角
∠AOB所对的弦为AB.
2.圆心角
∠AOB
所对的弧为
AB.
⌒
新知探究
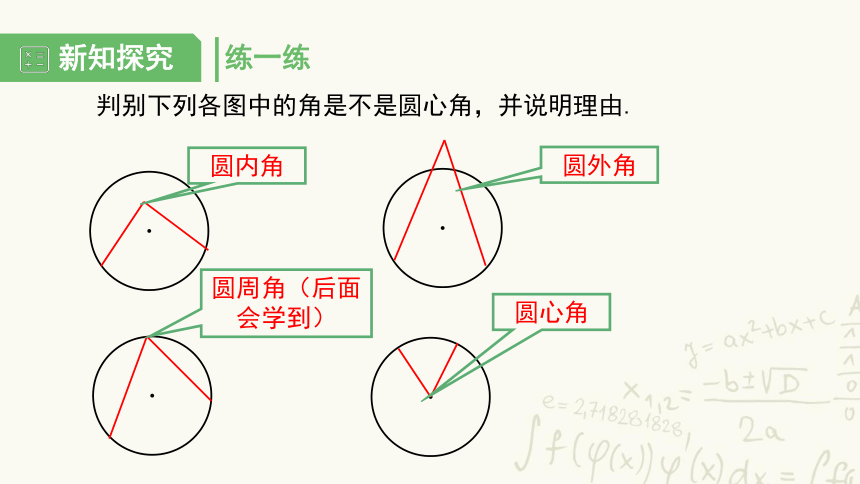
判别下列各图中的角是不是圆心角,并说明理由.
圆内角
圆外角
圆周角(后面会学到)
圆心角
练一练
新知探究
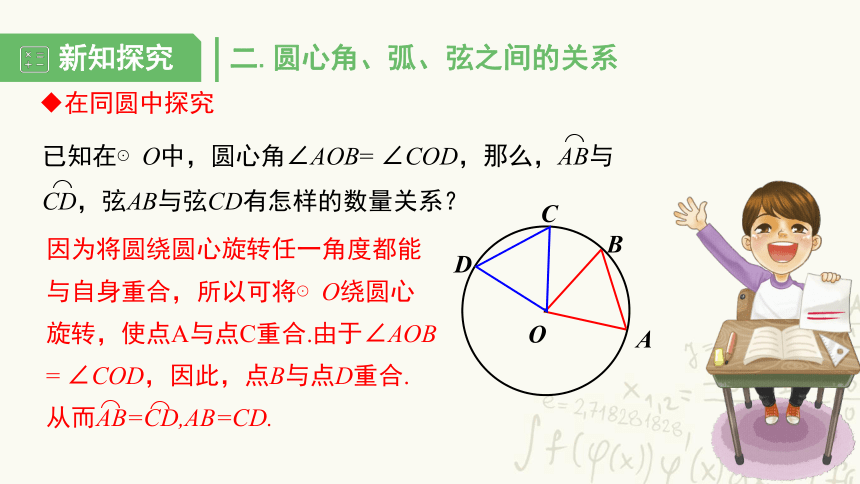
已知在⊙O中,圆心角∠AOB=
∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
C
·
O
A
B
D
⌒
因为将圆绕圆心旋转任一角度都能
与自身重合,所以可将⊙O绕圆心
旋转,使点A与点C重合.由于∠AOB
=
∠COD,因此,点B与点D重合.
从而AB=CD,AB=CD.
⌒
⌒
在同圆中探究
二.圆心角、弧、弦之间的关系
新知探究
O
·
A
B
如图,在等圆中,如果∠AOB=∠CO
′
D,你发现的等量关系是否依然成立?为什么?
·
O
′
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO'D,那么,AB=CD,弦AB=弦CD.
⌒
⌒
二.圆心角、弧、弦之间的关系
新知探究
归纳总结
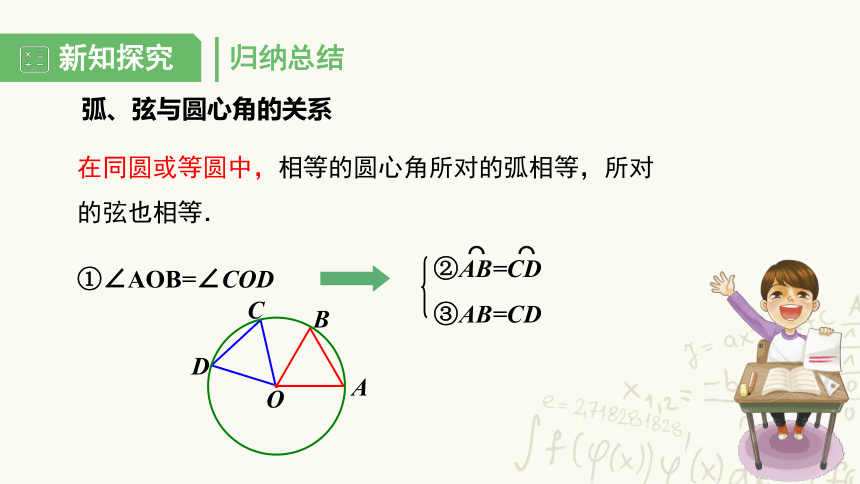
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒
⌒
③AB=CD
A
B
O
D
C
弧、弦与圆心角的关系
新知探究
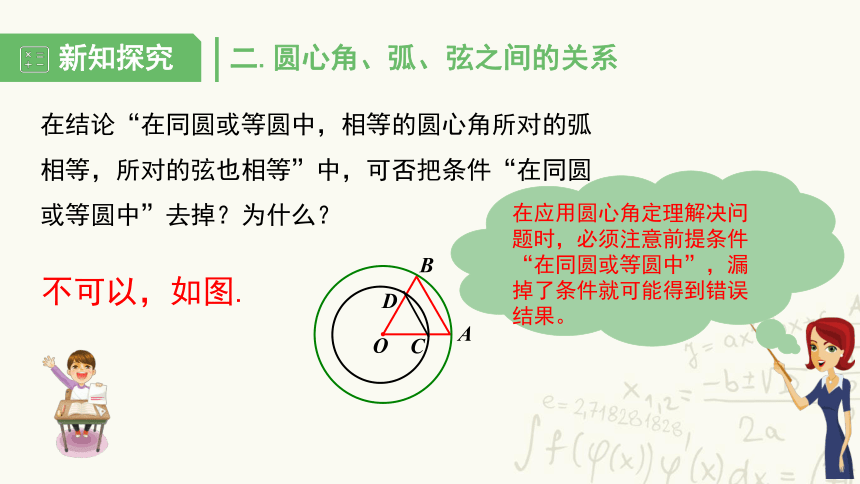
在结论“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
在应用圆心角定理解决问题时,必须注意前提条件“在同圆或等圆中”,漏掉了条件就可能得到错误结果。
二.圆心角、弧、弦之间的关系
新知探究
归纳总结
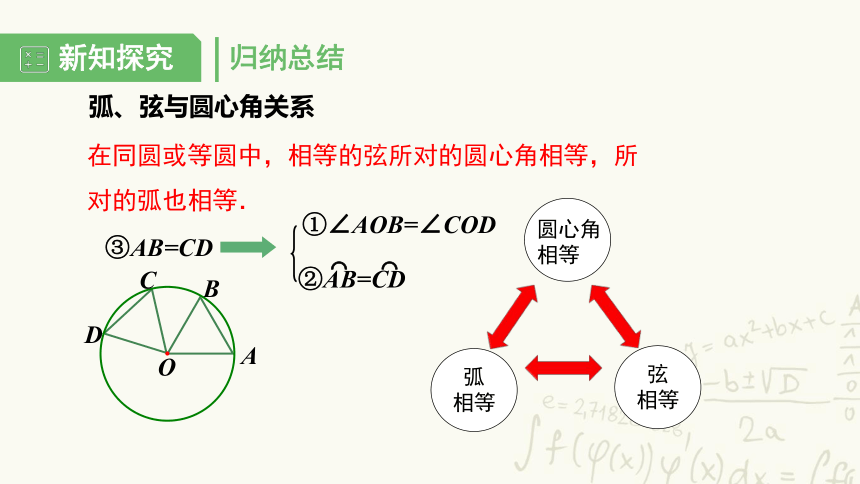
在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
弧、弦与圆心角关系
圆心角
相等
弦
相等
弧
相等
新知探究
归纳总结
在同圆或等圆中,如果两个圆心角、两条弧或两条弦中,有一组量相等,那么它们所对的其余各组量都分别相等.
新知探究
练一练
如图,C、D为半圆上的三等分点,则下列说法:
①AD=CD=BC
②∠AOD=∠DOC=∠BOC
③AD=CD=BC
④△AOD以O为中心顺时针旋转120°与△COB重合,正确的有(
)
A
A.4个
B.3个
C.2个
D.1个
A
B
O
D
C
⌒
⌒
⌒
新知探究
三.圆周角的定义
顶点在圆上,并且两边都与圆相交的角叫作圆周角.
(如∠BAC)
我们把∠BAC叫作BC所对圆周角,BC叫作圆周角∠BAC所对的弧.
⌒
⌒
新知探究
练一练
如图,点A,B,C在⊙O上,°,则∠OBC的度数为(
)。
·
A
B
C
O
A.40°
B.50°
C.80°
D.100°
A
新知探究
四.圆周角定理
图中的∠ABC、∠ADC和∠AEC都是AC所对的圆周角,我们知道在同圆或等圆中,相等的弧所对的圆心角相等,那么图中的三个圆周角有什么关系?
⌒
A
B
C
D
E
新知探究
四.圆周角定理
为了弄清楚这三个角的关系,我们先来研究一条弧所对的圆周角和圆心角的关系.
我猜测也相等
A
B
C
D
E
新知探究
想一想
如图,点A、B、C是☉O
上的点,请问图中哪些是圆周角?哪些是圆心角?
圆心角:∠BOC
圆周角:∠BAC
分别量出这些角的度数,你有什么发现?
∠BOC=2∠BAC
新知探究
想一想
变动点A的位置,看看上述结论是否依然成立?
A
A
A
变动点A的位置,圆周角的度数没有变化,它的度数恰好为同弧所对的圆心角的度数的一半.
新知探究
归纳总结
圆周角的度数等于它所对弧上的圆心角度数的一半.
新知探究
练一练
如图,△ABC是☉O的内接三角形,AB=AC,
,作CD∥AB,并与☉O相交于点D,连接BD,则的大小为(
)
A.
B.
C.
D.
·
A
B
C
O
D
A
新知探究
五.圆周角定理的推论
1.在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
2.直径所对的圆周角是直角;90°的圆周角所对的弦是直径.四边形的四个顶点都在同一个圆上,这样的四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆.圆内接四边形的对角互补.
03
典型例题
典型例题
1.将一个圆分割成3个扇形,它们的圆心角的度数比为1:2:3,则这三个扇形中圆心角度数最大的是(
)。
A.
B.
C.
D.
D
典型例题
2.如图,已知,则圆心角的度数为(
)。
A.
B.
C.
D.
D
·
A
B
C
O
典型例题
3.如图,点A,B,C,D在☉O上,∠AOC=140°,点B是AC的中点,则∠D的度数为(
)
A.70°
B.55°
C.35.5°
D.35°
D
·
A
B
C
O
D
04
拓展提高
拓展提高
如图,是圆的直径,AC=CD,
(1)△AOC是等边三角形么?
(2)求证OC∥BD.
解:
(1)
∠AOC=
∠COD=60°
又OA=OC
△AOC是等边三角形
⌒
⌒
A
B
O
D
C
⌒
⌒
△AOC是等边三角形
扩展提高
(2)由(1)知=
,
又
,
,
OC∥BD.
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
圆心角与圆周角
教学课件
湘教版九年级下册
01
新课导入
新课导入
在图片中存在着不同的角,同学们发现这些角有什么相同的特征码?
好像角的顶点都是在中心的。
今天,我们就让我们来学习一下这个顶点在中心的角吧!
02
新知探究
新知探究
一.圆心角的概念
O
A
B
M
1.圆心角:顶点在圆心,角的两边与圆相交的角叫圆心角,如∠AOB
.
3.圆心角
∠AOB所对的弦为AB.
2.圆心角
∠AOB
所对的弧为
AB.
⌒
新知探究
判别下列各图中的角是不是圆心角,并说明理由.
圆内角
圆外角
圆周角(后面会学到)
圆心角
练一练
新知探究
已知在⊙O中,圆心角∠AOB=
∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
C
·
O
A
B
D
⌒
因为将圆绕圆心旋转任一角度都能
与自身重合,所以可将⊙O绕圆心
旋转,使点A与点C重合.由于∠AOB
=
∠COD,因此,点B与点D重合.
从而AB=CD,AB=CD.
⌒
⌒
在同圆中探究
二.圆心角、弧、弦之间的关系
新知探究
O
·
A
B
如图,在等圆中,如果∠AOB=∠CO
′
D,你发现的等量关系是否依然成立?为什么?
·
O
′
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO'D,那么,AB=CD,弦AB=弦CD.
⌒
⌒
二.圆心角、弧、弦之间的关系
新知探究
归纳总结
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒
⌒
③AB=CD
A
B
O
D
C
弧、弦与圆心角的关系
新知探究
在结论“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
在应用圆心角定理解决问题时,必须注意前提条件“在同圆或等圆中”,漏掉了条件就可能得到错误结果。
二.圆心角、弧、弦之间的关系
新知探究
归纳总结
在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
弧、弦与圆心角关系
圆心角
相等
弦
相等
弧
相等
新知探究
归纳总结
在同圆或等圆中,如果两个圆心角、两条弧或两条弦中,有一组量相等,那么它们所对的其余各组量都分别相等.
新知探究
练一练
如图,C、D为半圆上的三等分点,则下列说法:
①AD=CD=BC
②∠AOD=∠DOC=∠BOC
③AD=CD=BC
④△AOD以O为中心顺时针旋转120°与△COB重合,正确的有(
)
A
A.4个
B.3个
C.2个
D.1个
A
B
O
D
C
⌒
⌒
⌒
新知探究
三.圆周角的定义
顶点在圆上,并且两边都与圆相交的角叫作圆周角.
(如∠BAC)
我们把∠BAC叫作BC所对圆周角,BC叫作圆周角∠BAC所对的弧.
⌒
⌒
新知探究
练一练
如图,点A,B,C在⊙O上,°,则∠OBC的度数为(
)。
·
A
B
C
O
A.40°
B.50°
C.80°
D.100°
A
新知探究
四.圆周角定理
图中的∠ABC、∠ADC和∠AEC都是AC所对的圆周角,我们知道在同圆或等圆中,相等的弧所对的圆心角相等,那么图中的三个圆周角有什么关系?
⌒
A
B
C
D
E
新知探究
四.圆周角定理
为了弄清楚这三个角的关系,我们先来研究一条弧所对的圆周角和圆心角的关系.
我猜测也相等
A
B
C
D
E
新知探究
想一想
如图,点A、B、C是☉O
上的点,请问图中哪些是圆周角?哪些是圆心角?
圆心角:∠BOC
圆周角:∠BAC
分别量出这些角的度数,你有什么发现?
∠BOC=2∠BAC
新知探究
想一想
变动点A的位置,看看上述结论是否依然成立?
A
A
A
变动点A的位置,圆周角的度数没有变化,它的度数恰好为同弧所对的圆心角的度数的一半.
新知探究
归纳总结
圆周角的度数等于它所对弧上的圆心角度数的一半.
新知探究
练一练
如图,△ABC是☉O的内接三角形,AB=AC,
,作CD∥AB,并与☉O相交于点D,连接BD,则的大小为(
)
A.
B.
C.
D.
·
A
B
C
O
D
A
新知探究
五.圆周角定理的推论
1.在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
2.直径所对的圆周角是直角;90°的圆周角所对的弦是直径.四边形的四个顶点都在同一个圆上,这样的四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆.圆内接四边形的对角互补.
03
典型例题
典型例题
1.将一个圆分割成3个扇形,它们的圆心角的度数比为1:2:3,则这三个扇形中圆心角度数最大的是(
)。
A.
B.
C.
D.
D
典型例题
2.如图,已知,则圆心角的度数为(
)。
A.
B.
C.
D.
D
·
A
B
C
O
典型例题
3.如图,点A,B,C,D在☉O上,∠AOC=140°,点B是AC的中点,则∠D的度数为(
)
A.70°
B.55°
C.35.5°
D.35°
D
·
A
B
C
O
D
04
拓展提高
拓展提高
如图,是圆的直径,AC=CD,
(1)△AOC是等边三角形么?
(2)求证OC∥BD.
解:
(1)
∠AOC=
∠COD=60°
又OA=OC
△AOC是等边三角形
⌒
⌒
A
B
O
D
C
⌒
⌒
△AOC是等边三角形
扩展提高
(2)由(1)知=
,
又
,
,
OC∥BD.
05
课堂小结
课堂小结
06
作业布置
作业布置
谢
谢
观
看
