湘教版数学九年级下册2.1 圆的对称性教学课件(共31张PPT)
文档属性
| 名称 | 湘教版数学九年级下册2.1 圆的对称性教学课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 23:46:55 | ||
图片预览







文档简介
(共31张PPT)
圆的对称性
教学课件
湘教版九年级下册
01
新课导入
新课导入
在日常生活中,我们常常见到圆形的物体,例如指南针、硬币、呼啦圈等都是圆的,可见圆的应用非常广泛。它为什么这么备受青睐呢?今天就让我们来学习一下“圆”的奥秘吧!
02
新知探究
新知探究
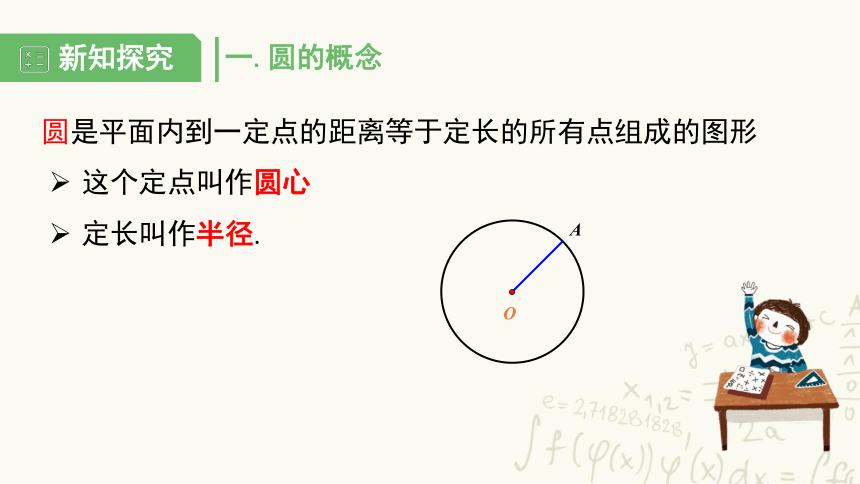
一.圆的概念
圆是平面内到一定点的距离等于定长的所有点组成的图形
·
定长叫作半径.
这个定点叫作圆心
O
A
新知探究
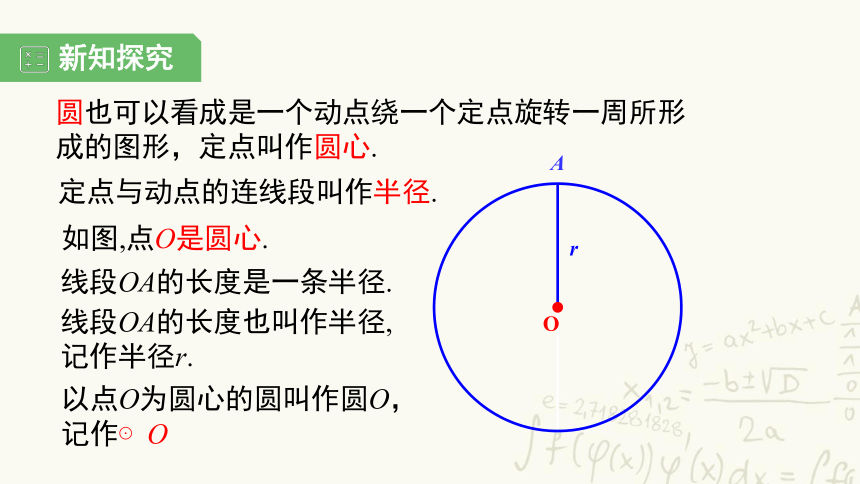
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O
定点与动点的连线段叫作半径.
如图,点O是圆心.
线段OA的长度是一条半径.
线段OA的长度也叫作半径,
记作半径r.
·
r
O
A
新知探究
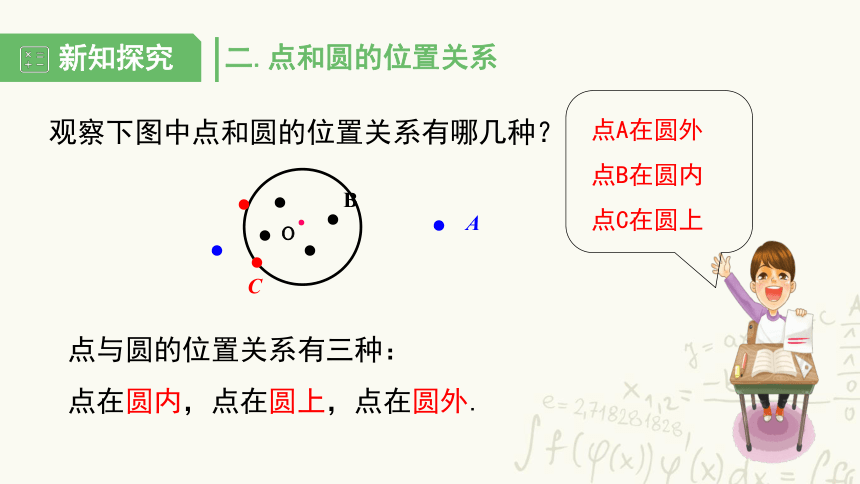
二.点和圆的位置关系
.
观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
.
B
.
.A
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
点A在圆外
点B在圆内
点C在圆上
新知探究
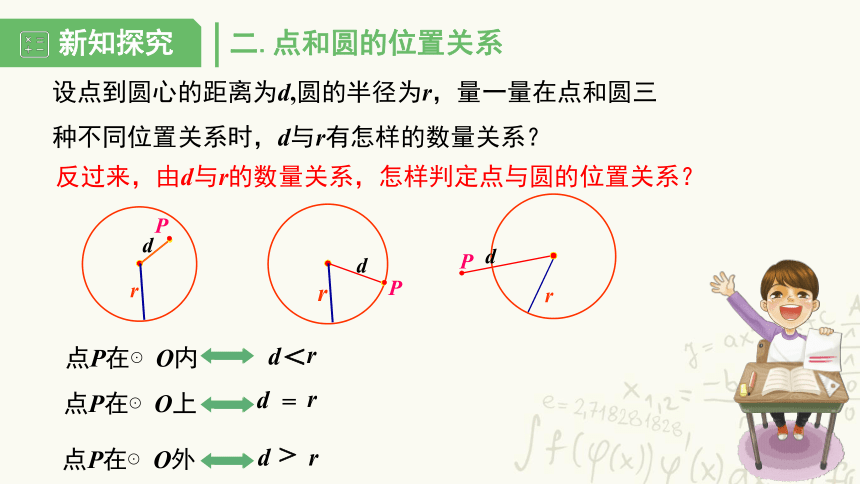
二.点和圆的位置关系
设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系?
点P在⊙O上
d=r
点P在⊙O内
d新知探究
归纳总结
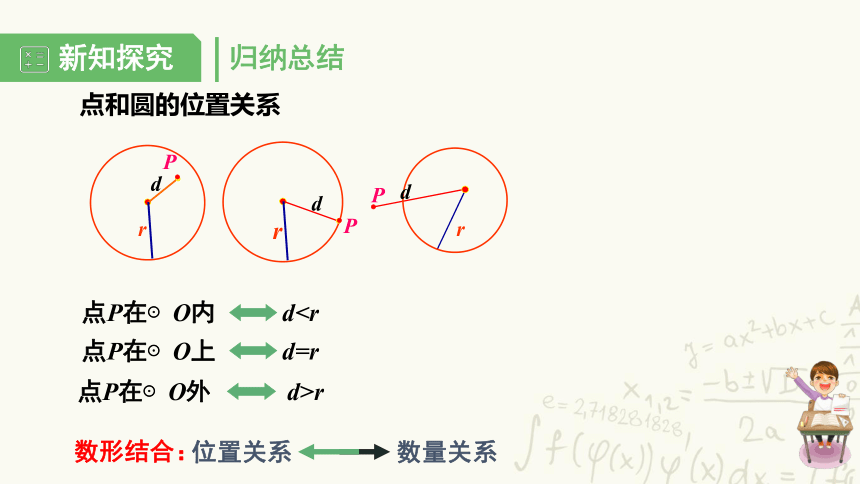
点和圆的位置关系
r
P
d
P
r
d
P
r
d
点P在⊙O外
d>r
数形结合:
位置关系
数量关系
新知探究
练一练
已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是(
)。
A.点P在⊙O内
B.点P在⊙O上
C.点P在⊙O外
D.无法判断
A
新知探究
三.圆的有关概念
弦:
·
C
O
A
B
连接圆上任意两点的线段
(如图中的AC,AB)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
◆弧:
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
◆劣弧与优弧
·
C
O
A
B
◆半圆
圆上任意两点间的部分叫做圆弧,简称弧,弧用符号“⌒”表示.
以A、B为端点的弧记作
AB
,读作
“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧.如图中的AC
;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
新知探究
练一练
下列说法错误的是
(
)
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
B
新知探究
归纳总结
1.根据圆的定义,“圆”指的是“圆周”,而不是“圆面”.
2.直径是圆中最长的弦.
附图解释:
·
C
O
A
B
连接OC,
在△AOC中,根据三角形三边关系有AO+OC>AC,
而AB=2OA,AO=OC,所以AB>AC.
新知探究
四.圆的对称性
这两个圆
用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
重合
能够重合的两个圆叫作等圆,
把能够互相重合的弧叫作等弧.
新知探究
四.圆的对称性
现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?
·
仍然重合
圆是中心对称图形,圆心是它的对称中心.
新知探究
四.圆的对称性
在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
仍然重合
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
新知探究
想一想
为什么车轮要做成圆形的?
中心与路面距离相等
中心与边缘距离相等
中心与边缘距离不相等
中心与路面距离不相等
03
典型例题
典型例题
1.下列说法错误的是(
)
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆是等圆
C
典型例题
2.自行车车轮要做成圆形,实际上是根据圆的哪个特征(
)。
A.圆是轴对称图形
B.直径是圆中最长的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
C
典型例题
3.若圆的半径为5,点的坐标为(3,4),点的坐标为(5,8),则点的位置为(
)
A
A.在圆内
B.在圆上
C.在圆外
D.不确定
典型例题
4.在平面直角坐标系xOy中,若点P(3,4)在⊙O内,则⊙O的半径r的取值范围是(
)。
A.0B.r>4
C.0D.r>5
D
04
拓展提高
拓展提高
1.如图,在△ABC中,∠C=90°,AB=4,以点C为圆心,2为半径作⊙C,则AB的中心点O与⊙C的位置关系是(
)。
B
A.点在⊙C外
B.点在⊙C上
C.点在⊙C
D.不能确定
A
B
C
O
拓展提高
解:方程x2-2x+d=0有实数根,
△=4-4d≥0,
d≤1,d≤r.
当d当d=r时,点P在⊙O上。
点P在⊙O内或在⊙O上。
2.已知⊙O的半径r为1,点P与点O的距离为d,且方程x2-2x+d=0有实数根,判断点P与⊙O的位置关系。
点P在⊙O内或在⊙O上
05
课堂小结
课堂小结
06
作业布置
作业布置
完成课本习题2.1节A、B组
谢
谢
观
看
圆的对称性
教学课件
湘教版九年级下册
01
新课导入
新课导入
在日常生活中,我们常常见到圆形的物体,例如指南针、硬币、呼啦圈等都是圆的,可见圆的应用非常广泛。它为什么这么备受青睐呢?今天就让我们来学习一下“圆”的奥秘吧!
02
新知探究
新知探究
一.圆的概念
圆是平面内到一定点的距离等于定长的所有点组成的图形
·
定长叫作半径.
这个定点叫作圆心
O
A
新知探究
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O
定点与动点的连线段叫作半径.
如图,点O是圆心.
线段OA的长度是一条半径.
线段OA的长度也叫作半径,
记作半径r.
·
r
O
A
新知探究
二.点和圆的位置关系
.
观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
.
B
.
.A
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
点A在圆外
点B在圆内
点C在圆上
新知探究
二.点和圆的位置关系
设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系?
点P在⊙O上
d=r
点P在⊙O内
d
归纳总结
点和圆的位置关系
r
P
d
P
r
d
P
r
d
点P在⊙O外
d>r
数形结合:
位置关系
数量关系
新知探究
练一练
已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是(
)。
A.点P在⊙O内
B.点P在⊙O上
C.点P在⊙O外
D.无法判断
A
新知探究
三.圆的有关概念
弦:
·
C
O
A
B
连接圆上任意两点的线段
(如图中的AC,AB)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
◆弧:
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
◆劣弧与优弧
·
C
O
A
B
◆半圆
圆上任意两点间的部分叫做圆弧,简称弧,弧用符号“⌒”表示.
以A、B为端点的弧记作
AB
,读作
“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧.如图中的AC
;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
新知探究
练一练
下列说法错误的是
(
)
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
B
新知探究
归纳总结
1.根据圆的定义,“圆”指的是“圆周”,而不是“圆面”.
2.直径是圆中最长的弦.
附图解释:
·
C
O
A
B
连接OC,
在△AOC中,根据三角形三边关系有AO+OC>AC,
而AB=2OA,AO=OC,所以AB>AC.
新知探究
四.圆的对称性
这两个圆
用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
重合
能够重合的两个圆叫作等圆,
把能够互相重合的弧叫作等弧.
新知探究
四.圆的对称性
现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?
·
仍然重合
圆是中心对称图形,圆心是它的对称中心.
新知探究
四.圆的对称性
在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
仍然重合
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
新知探究
想一想
为什么车轮要做成圆形的?
中心与路面距离相等
中心与边缘距离相等
中心与边缘距离不相等
中心与路面距离不相等
03
典型例题
典型例题
1.下列说法错误的是(
)
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆是等圆
C
典型例题
2.自行车车轮要做成圆形,实际上是根据圆的哪个特征(
)。
A.圆是轴对称图形
B.直径是圆中最长的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
C
典型例题
3.若圆的半径为5,点的坐标为(3,4),点的坐标为(5,8),则点的位置为(
)
A
A.在圆内
B.在圆上
C.在圆外
D.不确定
典型例题
4.在平面直角坐标系xOy中,若点P(3,4)在⊙O内,则⊙O的半径r的取值范围是(
)。
A.0
C.0
D
04
拓展提高
拓展提高
1.如图,在△ABC中,∠C=90°,AB=4,以点C为圆心,2为半径作⊙C,则AB的中心点O与⊙C的位置关系是(
)。
B
A.点在⊙C外
B.点在⊙C上
C.点在⊙C
D.不能确定
A
B
C
O
拓展提高
解:方程x2-2x+d=0有实数根,
△=4-4d≥0,
d≤1,d≤r.
当d
点P在⊙O内或在⊙O上。
2.已知⊙O的半径r为1,点P与点O的距离为d,且方程x2-2x+d=0有实数根,判断点P与⊙O的位置关系。
点P在⊙O内或在⊙O上
05
课堂小结
课堂小结
06
作业布置
作业布置
完成课本习题2.1节A、B组
谢
谢
观
看
