全等三角形全章学案
图片预览


文档简介
第十一章 全等三角形
11.1全等三角形
学习目标
1.知道什么是全等形、全等三角形;
2.能熟练找出全等三角形的对应元素,能用符号正确地表示两个三角形全等;
3.掌握全等三角形的性质.
重点: 全等三角形的概念、性质。
难点: 对应边和对应角的确定。
自主学习
一、全等形、全等三角形的概念
阅读课本P2内容,回答课本思考问题,并完成下面填空:
1. 能够完全重合的两个图形叫做 .
全等图形的特征:全等图形的 和 都相同.
2.能够完全重合的两个三角形叫做 .
二、全等三角形的对应元素及表示
阅读课本P3第一个思考及下面两段内容,完成下面填空:
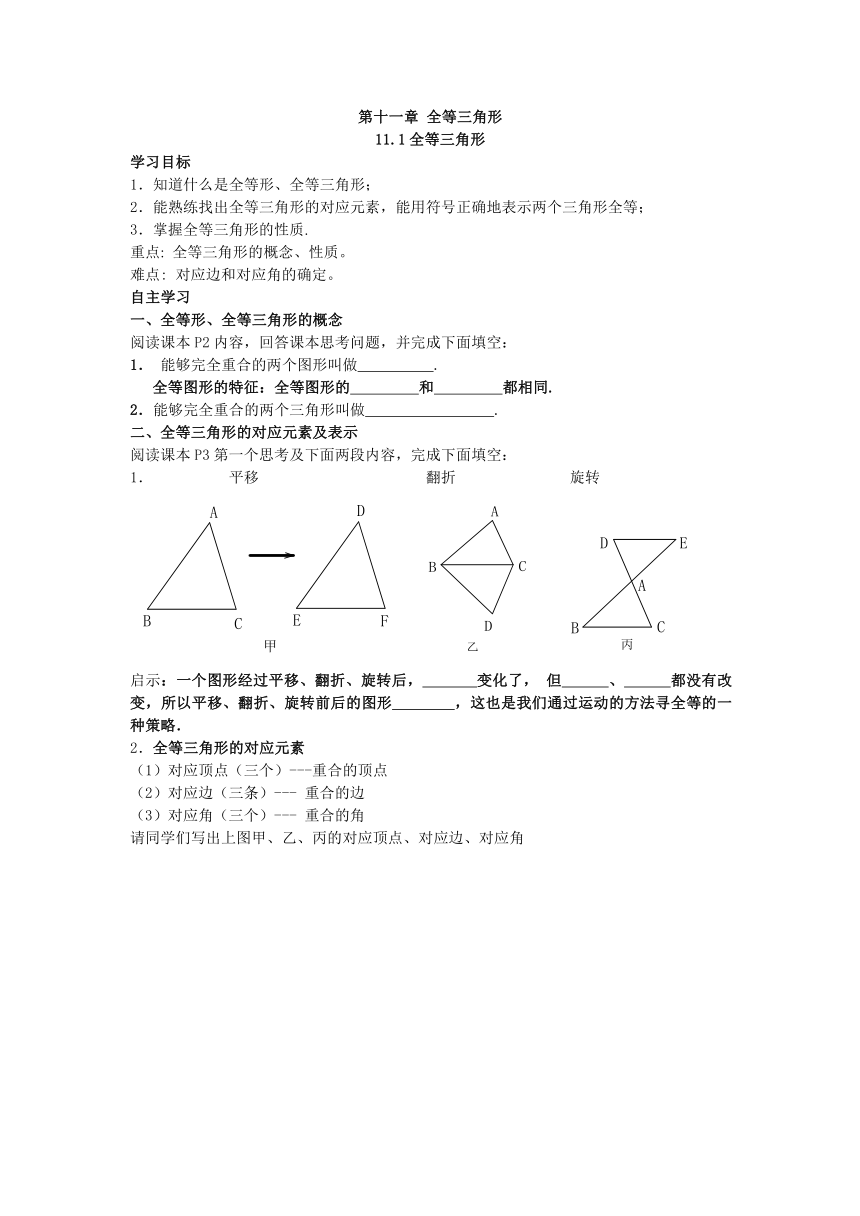
1. 平移 翻折 旋转
启示:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻全等的一种策略.
2.全等三角形的对应元素
(1)对应顶点(三个)---重合的顶点
(2)对应边(三条)--- 重合的边
(3)对应角(三个)--- 重合的角
请同学们写出上图甲、乙、丙的对应顶点、对应边、对应角
图甲: 对应边是: 对应顶点是: 对应角是:
图乙:
对应边是:
对应顶点是: 对应角是:
图丙:对应顶点是: 对应边是:
对应角是:
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(5)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
3.“全等”用“≌”表示,读作“全等于”
如图甲记作:△ABC≌△DEF 读作:△ABC全等于△DEF
如图乙记作: 读作:
如图丙记作: 读作:
注意:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
三、全等三角形的性质
阅读课本P3第二个思考及下面内容,完成下面填空:
全等三角形的性质:
全等三角形的 相等, 相等.
练习
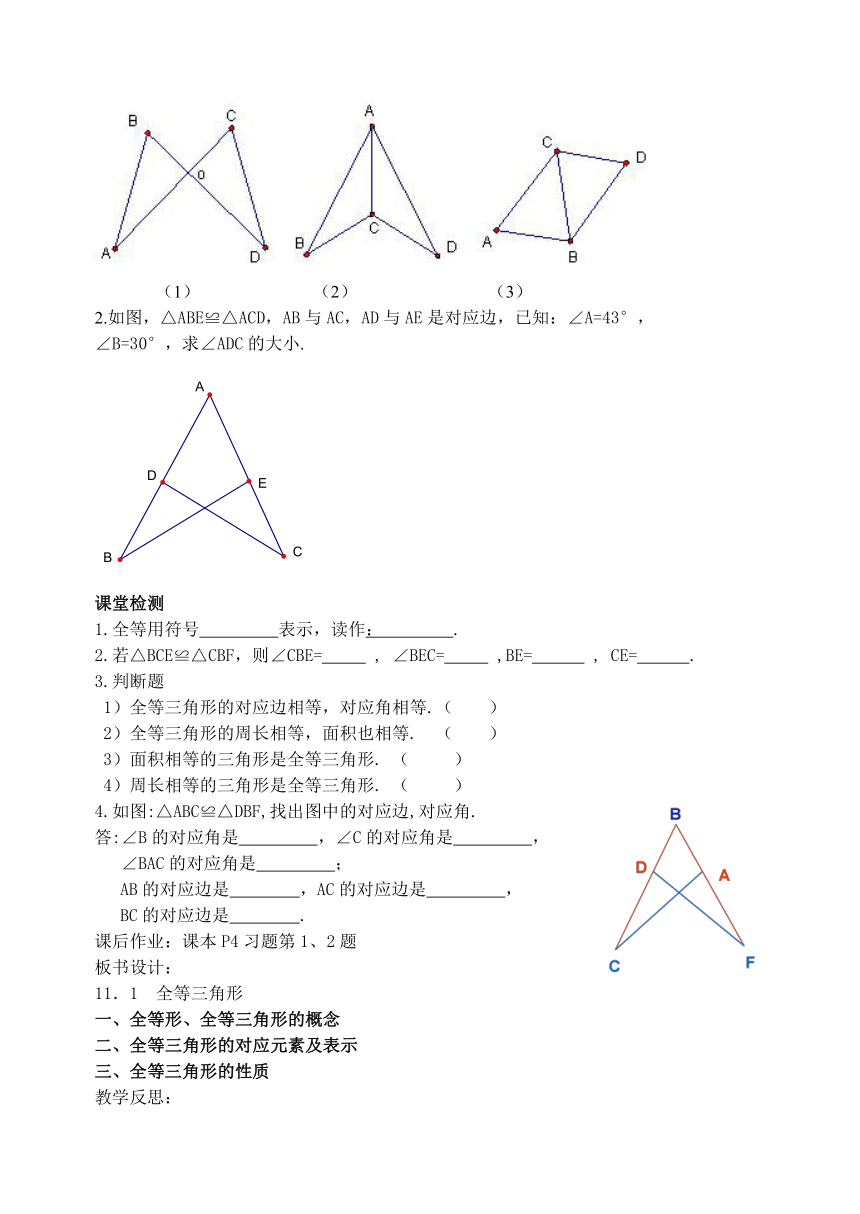
1.如图1,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
图1 图2
2.如图2,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
课堂小结
本节课你有哪些收获?
巩固练习
1.下面是两个全等的三角形,按下列图形的位置摆放,指出它们的对应顶点、对应边、对应角.
(1) (2) (3)
2.如图,△ABE≌△ACD,AB与AC,AD与AE是对应边,已知:∠A=43°,
∠B=30°,求∠ADC的大小.
课堂检测
1.全等用符号 表示,读作: .
2.若△BCE≌△CBF,则∠CBE= , ∠BEC= ,BE= , CE= .
3.判断题
1)全等三角形的对应边相等,对应角相等.( )
2)全等三角形的周长相等,面积也相等. ( )
3)面积相等的三角形是全等三角形. ( )
4)周长相等的三角形是全等三角形. ( )
4.如图:△ABC≌△DBF,找出图中的对应边,对应角.
答:∠B的对应角是 ,∠C的对应角是 ,
∠BAC的对应角是 ;
AB的对应边是 ,AC的对应边是 ,
BC的对应边是 .
课后作业:课本P4习题第1、2题
板书设计:
11.1 全等三角形
一、全等形、全等三角形的概念
二、全等三角形的对应元素及表示
三、全等三角形的性质
教学反思:
11.2.1三角形全等的判定
学习目标
1.理解三边对应相等的两个三角形全等的内容.
2.会运用“边边边”条件证明两个三角形全等.
3. 会作一个角等于已知角.
自主学习
一、课前准备
1. 叫做全等三角形
2.全等三角形的 和 相等
3.将△ABC沿直线BC平移,得到△DEF,说出你得到的结论,说明理由?
如果AB=5, ∠A=55°, ∠B=45°,那么DE= ,∠F= .
二、自主探究
自主探究三角形全等的条件:
阅读课本P6探究2之前,回答下面问题:
通过探究
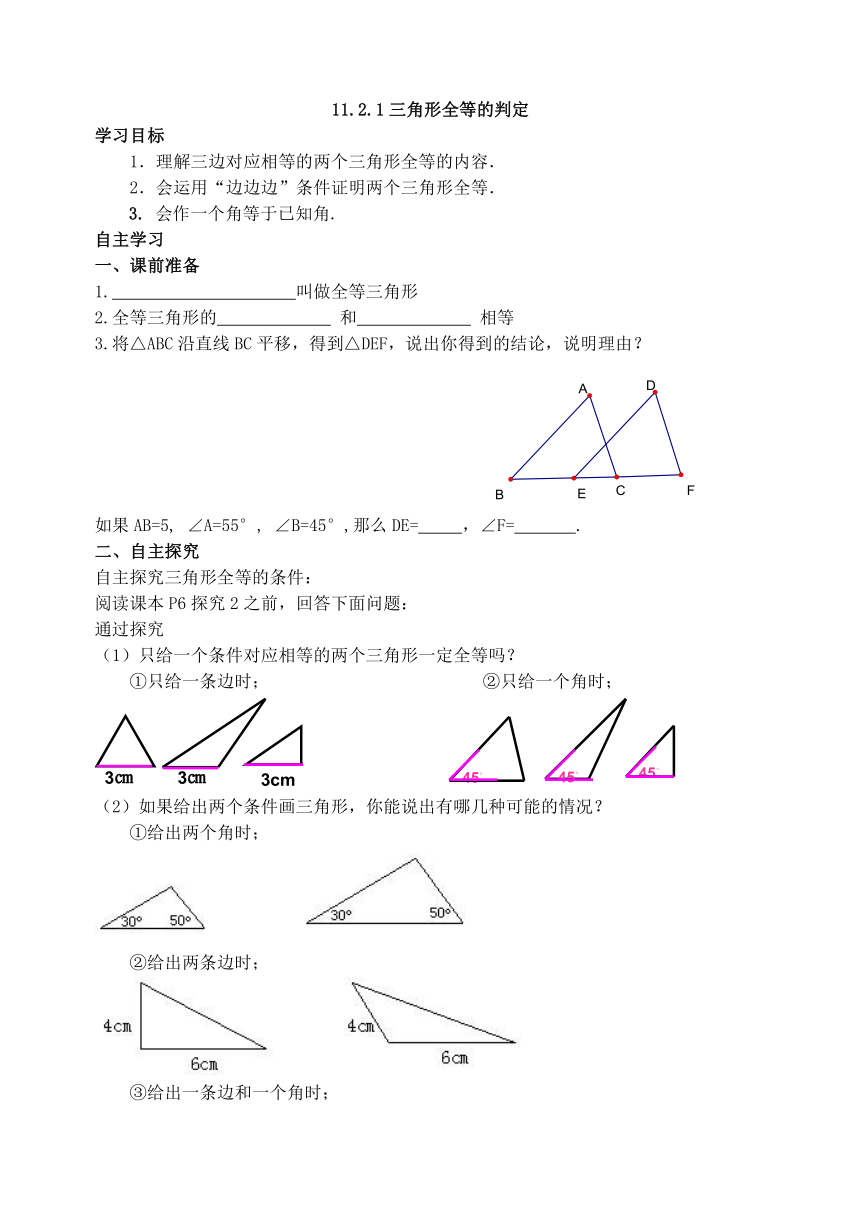
(1)只给一个条件对应相等的两个三角形一定全等吗?
①只给一条边时;
②只给一个角时;
(2)如果给出两个条件画三角形,你能说出有哪几种可能的情况?
①给出两个角时;
②给出两条边时;
③给出一条边和一个角时;
(3)由上面的几种情景,两个三角形满足一个或两个条件时,它们一定全等吗?
(4)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况?
①我们先来探究两个三角形三个角相等的情况:
②画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?
③上面的探究反映了什么规律?
阅读课本P6-7探究2至例1前,回答下面问题:
的两个三角形全等,简写为“ ”或“ ”.
三、例题学习
阅读课本P7例1,学习“边边边”证明两个三角形全等的格式.
巩固练习
1. 如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC(2)∠B=∠D
证明:
(1)在△ABC和△ADC中
(公共边)
∴△ABC≌△ADC( )
(2)∵△ABC≌△ADC
∴∠B=∠D( )
2.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
证明:
四、作一个角等于已知角
阅读课本P7最后一段至P8,回答书中问题.
课堂小结
本节课你有哪些收获?
课堂检测
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
证明:
课后作业:课本P15习题第1、2题
板书设计:
11.2.1 三角形全等的条件(一)
一、三角形全等的条件
三边对应相等的两三角形全等(SSS)
二、例题
三、作一个角等于已知角
教学反思:
11.2.2全等三角形的识别(二)(SAS)
学习目标:会运用“边角边”公理证明三角形全等的简单问题
重难点:1、会运用“边角边”公理证明三角形全等的简单问题
2、分清用两边一角证明三角形相似和全等的不同。
自学过程:
知识回顾:
一、判别三角形相似的方法之二:
1、如果两个三角形有 _____边对应______,并且____相等,那么这两个三角形相似.
新课讲解:
做一做 以图24.2.5中的两条线段和一个角画一个三角形,使该角恰为这两条线段的夹角.
步骤:
画一线段AB使它的长度等于4cm.
以点A为顶点,作∠BAP=45°,在射线AP上截取AC=3cm,
连结BC.△ABC即为所求.
把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?
换两条线段和一个角,用同样的方法试试,是否有同样的结论.
A C
A B
A
这样我们就得到识别三角形全等的另一种简便的方法
如果两个三角形有 _____边及其______分别对应____,那么这两个三角形全等.简记为(S.A.S.).
对比判别三角形相似的方法
如果两个三角形有 _____边对应______,并且____相等,那么这两个三角形相似.
例2 如图11-1,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
做一做 如图24.2.7,已知两条线段和一个角,以这两条线段为边,以这个角为其中一条边的对角,画一个三角形.
图24.2.7
把你画的三角形与其他同学画的三角形进行比较,所有的三角形一定都会全等吗?
练 习
根据题目条件,判断下面的三角形是否全等?
(3) (4)
点M是等腰梯形ABCD底边AB的中点,△AMD和△BMC全等吗?试说明你的理由?
综合练习:
填空:
如图11-2,AB=AD,AC=AE,
则可得△ABC≌____
其理由是______
2、如图(1):OA=OD,OB=OC,求证:△ABO≌△DCO
证明: OA=OD OB=OC( )
____=_____( )
△ABO≌△DCO( )
3、如图(2):已知AB=DC,∠ABC=∠DCB,求证:AC=BD
证明:AB=DC,∠ABC=∠DCB ( )
BC=________( )
△BCD≌_______,( )
AC=________( )
如图(1) 如图(2)
选择:
1、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是( )
A ∠A B ∠B C ∠C D ∠B或∠D
l
2、如图:直线l是四边形ABCD的对称轴,如果,有下列 A
结论:(1)AB∥DC(2)AB=BC(3)ABBC(4) AO=OC, B O D
其中正确的结论有( )
A 1个 B 2个 C 3个 D 4个 C
3、具有下列条件的两个等腰三角形,不能判定它们全等的是( )
A 顶角、一腰对应相等 B 底边、一腰对就相等
C 两腰对应相等 D 一腰、一底角、一底边对应相等
△ABC和△A′B′C′边角条件如图:那么这两个三角形( ) C′
A全等 B不全等
C不一定全等 D相似
证明:1、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?
2、已知:AD=BC,∠ADC=∠BCD.求证: ∠BDC=∠ACD.
3、如图,AE=DB,BC=EF,BC∥EF,说明△ABC和△DEF全等的理由.
4、如图:点M是等腰梯形ABCD底边AB上的中点,则MD与MC的大小有何关系,试说明理由。
5、已知点A、B、C、D在同一条直线上,AB=CD, ∠D=∠ECA,试问:AE与BF的大小关系,并说明理由。
6、如图:在△ABC中,AB=AC, ∠BAC=90°,在AB上取点P,边CA的延长线上取点Q,使AP=AQ,边CP与BQ交于点S,求证:△CAP≌△BAQ
7、如图,AB=AD,AC=AE,∠BAE=∠DAC, △ABC与△ADE全等吗?并说明理由。
11.2.3 全等三角形的识别(三)(ASA及AAS)
学习目标:会运用“角边角”公理及其推论证明三角形全等的简单问题
重难点:能灵活运用“角边角”公理及其推论证明三角形全等的简单问题
自学过程:
做一做 如图24.2.9,已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.
步骤:
一线段AB使它的长度等于4cm.
分别以点A、B为顶点,作∠BAP=40°∠ABQ=60°,AP、BQ相交于点C,
△ABC即为所求.
把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
换两个角和一条线段, 用同样的方法试试看,是否有同样的结论.
A
B
A B
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的_______及其____分别对应_____,那么这两个三角形全等.简记为(A.S.A.).
例3 如图所示,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC≌△DCB.
解 ∠ABC=∠DCB,∠ACB=∠DBC,
BC是______,
______( )
思 考
如图24.2.11,如果两个三角形有两个角及其中一个角的对边分别对应相等,
那么这两个三角形是否一定全等?
图24.2.11
你的结论是______________________________________
证明: ∠A=∠D,∠C=∠F,
∠B=180°-______,∠E=180°-____,
∠____=∠______
又∠___=∠___,AB=____
△ABC≌△DEF.( )
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的_______及其____分别对应_____,那么这两个三角形全等.简记为(A.A.S.).
小结: 如果知道两个三角形的两个角及一条边分别对应相等,这时应该有两种不同的情况: 一种情况是两个角及两角的____(ASA); 另一种情况是两个角及其中一角的___(AAS),两种情况都可以证明三角形全等。如图24.2.8所示.
图24.2.8
练 习
填空:
1、如图:D是△ABC的边AB上一点,DE交AC于点E,交CF于点 F,DE=FE,FC∥AB, 求证:AE=CE
证明: FC∥AB( ) ∴∠_____=∠_____,
∠_____=∠_____, 又 DE=FE( )
∴△AED≌____( )
∴AE=CE( )
2、如图:点B、F、C、E在同一条直线上,FB=CE,
AB∥ED,AC∥FD,求证:AB=DE
证明: FB=CE( )
FB+___=CE+__( )
即:____=____
AB∥ED,AC∥FD
∠ABC=∠_______,∠ACB=∠_______
△ABD≌________,( )
AB=DE,( )
3、如图:AB=CD,AD=BC,EF过BD的中点O,求证:△OBF≌△ODE
证明:AB=CD,AD=BC( )
_________=__________( )
△ABD≌________,( )
∠CBD=_______
EF过BD的中点O( )
______=__________
又∠FOB=∠_____( )
△OBF≌_______( )
选择
1、下列说法中,正确的是( )
A所有的等腰三角形全等 B有两边对应相等的两个等腰三角形全等
C有一边对应相等的两个等腰三角形全等 D腰和顶角对应相等的两个等腰三角形全等
2、在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A 一定不全等 B 一定全等 C 不一定全等 D 以上都不对
3、如图:点E在△ABC外部,点D在BC边上,DE
交AC于F,若∠1=∠2=∠3,AC=AE,则( )
A △ABD≌△AFD B △AFE≌△ADC
C △AFE≌△DFC D △ABC≌△ADE
4、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )
A(1) (2) (3) B (1) (2) (5) C (1) (3) (5) D(2) (5) (6)
三、证明与计算:
根据题目条件,判别下面的两个三角形是否全等,并说明理由.
△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.
3、如图,AB=DE,AC∥DF,BC∥EF,△ABC与△DEF全等吗?试说明理由.
4、如图,∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?试说明理由。
5、已知: 如图,∠C=∠D,CE=DE.求证: ∠DAB=∠ABC.
6、已知: 如图,∠BDA=∠CEA,AE=AD.求证: AB=AC.
7、已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC, ∠B=∠C,求证:BD=CE
11.2.4 全等三角形的识别(四)(HL)
学习目标:会运用“斜边、直角边公理” 证明三角形全等的简单问题
重难点:
1、会运用“斜边、直角边公理”(HL) 证明三角形全等的简单问题
2、了解SSS、SAS、ASA、AAS也适用于直角三角形。
自学过程:
知识回顾:
一、判别三角形相似的方法之三:
如果一个三角形的_______分别与另一个三角形的_______对应相等,那么这两个三角形相似.
我们知道,对于两个三角形,有“边、边、角”对应相等,是不能保证它们全等的.但是,在两个直角三角形中,当斜边及一条直角边分别对应相等时,也具有“边、边、角”对应相等的条件,这时这两个直角三角形是否全等呢?
做一做 试以24.2.12中的两条线段AC、AB分别为直角边和斜边画一个直角三角形.
步骤:
画∠MCN=90°,
在射线CM上截取AC的长度,
以点A为圆心,以线段AB的长为半径画圆弧,交射线CN于点B,
连结AB,△ABC即为所求.
把你画的图形与周围的同学画的比较一下,所画的图形都全等吗?请按照下题的步骤证明你的结论。
如图,AC=DF,AB=DE,∠C=∠F=90°,试说明△ABC≌△DEF.
∠C=∠F=90°
BC=_________,EF=____________(勾股定理)
又 AC=DF,AB=DE,
_____=____
又∠__=∠__,AC=____
△ABC≌△DEF.( )
由此可以得到如下结论:
如果两个直角三角形的_____及一条______分别对应相等,那么这两个直角三角形全等. 称为斜边、直角边公理,简记为(H.L.).
注意:
1、斜边、直角边公理(HL)只能用于证明直角三角形的全等,对于其它三角形不适用。
2、SSS、SAS、ASA、AAS适用于任何三角形,包括直角三角形。
例4 如图24.2.13,AB是圆O的直径,AC=AD,试说
明△ABC和△ABD全等.
解 AB为⊙O的直径
∠ACB=∠___=__°.
又AC=AD,___=___,
△ABC≌△ABD.( )
练 习
如图,AC=AD,∠C=∠D=90°,试说明BC与BD相等.
以下面格点图中的格点为顶点,画出所有的直角三角形,并说明哪些直角三角形是全等的.
(第2题)
综合练习:
一、填空:
两条直角边对应相等的两个直角三角形______,理由是________
有一条边和一个锐角对应相等的两个直角三角形_____,理由是______
如图(1):BA⊥AC,CD∥AB,AB=CE,BC=DE,则△CDE≌______,
理由是_____,且有∠ACB=________,∠ABC=_______,
由此可知BC与DE互相__________
如图:AD、A′D′分别是锐角△ABC和△A′B′C′
中BC,B′C′边上的高,且AB=A′B′,AD=A′D′,若
使△ABC≌△A′B′C′,需补充条件是______
(只需填写一个你认为适当的条件)
二、选择:
1、两个直角三角形全等的条件是( )
A一锐角对应相等B两锐角对应相等C一条边对应相等D两条边对应相等
2、判断下列命题:(1)在Rt△ABC中,两锐角互余(2)有两个锐角不互余的三角形不是直角三角形(3)一条直角边对应相等的两个直角三角形全等(4)有两个锐角对应相等的两个直角三角形全等,其中正确的有( )
A 1个 B 2个 C 3个 D 4个
3、下列说法正确的有( )
(1)两条直角边对应相等的两个直角三角形全等(2)一条边和一个锐角对应相等的两个直角三角形全等(3)两条边对应相等的两个直角三角形全等(4)两个锐角对应相等的两个直角三角形全等。
A 1个 B 2个 C 3个 D 4个
4、在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=A′B′,那么下列结论中正确的是( )
A AC=A′C′ B BC=B′C′ C AC=B′C′ D ∠A=∠A′
下列叙述的图形中,是全等三角形的只有(
A 两个含60°角的直角三角形 B 腰对应相等的两个等腰三角形
C 有一边相等的两个等边三角形 D 面积相等的两个直角三角形
6、如图:△ABC中,∠C=90°,AC=BC,AD平分∠CAB,
交BC于D点,DE⊥AB于点E,且AB=60cm,则△BED的
周长为( )
A 100cm B 80cm C 60cm D 40cm
证明:
1、如图:CE⊥AB,DF⊥AB,垂足分别为EF,AC∥DB,且AC=BD,求证:CE=DF
2、如图:△ABC是等腰三角形,AB=AC,AD是高,
求证(1)BD=DC(2)∠BAD=∠CAD
3、如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,求证(1)AE=CF(2)AB∥CD
4、如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足为E、F,求证:EB=FC
5、如图:在Rt△ABC和Rt△A′B′C′中,∠ACB=∠A′C′B′=90°,CDAB,C′D′A′B′,且CD=C′D′,BC=B′C′,求证:Rt△ABC≌Rt△A′B′C′
11.3角平分线的性质
自学目标 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网" \t "_blank ):
(1)掌握角平分线的性质定理;
(2)能够运用性质定理证明两条线段相等;
(3)角平分线的性质定理及它的应用。
重难点 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网" \t "_blank ):角平分线的性质定理及它的应用。
自学过程:
一、复习:
1、判断两个三角形全等的方法:
(1)三边分别相等的两个三角形全等。
(2)有两边级其夹角对应相等的两个三角形全等。
(3)有两角及其夹边对应相等的两个三角形全等。
(4)有两个角及其中一角的对边对应相等的两个三角形全等。
(5)有一条直角边和斜边对应相等的两个直角三角形全等。
2、练习:根据题目的结论,添加相应的条件。
(1)如上图,AB=DE,AC=DF,______=_______,那么根据(SSS)可得
(2)如上图,AB=DE,AC=DF,______=_______,那么根据(SAS)可得
(3)如上图,AB=DE,______=______,______=_______,那么根据(ASA)可得
(4)如上图,AB=DE,______=______,_______=_______,那么根据(AAS)可得
(5)如右图,,_____=_____,
_______=_______,那么根据(HL)
可得
三、“角平分线上的点到这个角两边的距离相等”
请你自己设计出一条几何证明题,去证明上面的命题是否正确:
小光已经做出了一些步骤,请你帮他补充完整:
解: 如右图:
已知:__________________,
___________________
求证:______=_______
证明:
归纳:从上面的我们可知道“角平分线上的点到这个角两边的距离相等”这是一个_________(填“真”或“假”)命题。
练习:根据上面定理完成书本P21 思考。
四:把前面的定理反过来可得:“角的内部到角两边的距离相等的点在角的平分线上”
请你自己设计出一条几何证明题,去证明上面的命题是否正确:
小白已经做出了一些步骤,请你帮他补充完整:
解:如右图,过______做射线
已知:,;
并且_______=_______
求证:_____是的平分线
证明:
归纳:从上面的我们可知道“角的内部到角两边的距离相等的点在角的平分线上”这是一个_________(填“真”或“假”)命题。
五、练习:
A组:
1、请你利用尺规作图,画出的平分线
B组:
书P22页习题11.3第1----5题。(可做在书本上)
C组:请你利用尺规作图在内部找一个点,
使这个点到三边距离相等
3㎝
3㎝
3cm
45
45
45
300
700
800
300
800
700
A
B
C
D
B
C
D
A
PAGE
11.1全等三角形
学习目标
1.知道什么是全等形、全等三角形;
2.能熟练找出全等三角形的对应元素,能用符号正确地表示两个三角形全等;
3.掌握全等三角形的性质.
重点: 全等三角形的概念、性质。
难点: 对应边和对应角的确定。
自主学习
一、全等形、全等三角形的概念
阅读课本P2内容,回答课本思考问题,并完成下面填空:
1. 能够完全重合的两个图形叫做 .
全等图形的特征:全等图形的 和 都相同.
2.能够完全重合的两个三角形叫做 .
二、全等三角形的对应元素及表示
阅读课本P3第一个思考及下面两段内容,完成下面填空:
1. 平移 翻折 旋转
启示:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻全等的一种策略.
2.全等三角形的对应元素
(1)对应顶点(三个)---重合的顶点
(2)对应边(三条)--- 重合的边
(3)对应角(三个)--- 重合的角
请同学们写出上图甲、乙、丙的对应顶点、对应边、对应角
图甲: 对应边是: 对应顶点是: 对应角是:
图乙:
对应边是:
对应顶点是: 对应角是:
图丙:对应顶点是: 对应边是:
对应角是:
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(5)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
3.“全等”用“≌”表示,读作“全等于”
如图甲记作:△ABC≌△DEF 读作:△ABC全等于△DEF
如图乙记作: 读作:
如图丙记作: 读作:
注意:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
三、全等三角形的性质
阅读课本P3第二个思考及下面内容,完成下面填空:
全等三角形的性质:
全等三角形的 相等, 相等.
练习
1.如图1,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
图1 图2
2.如图2,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
课堂小结
本节课你有哪些收获?
巩固练习
1.下面是两个全等的三角形,按下列图形的位置摆放,指出它们的对应顶点、对应边、对应角.
(1) (2) (3)
2.如图,△ABE≌△ACD,AB与AC,AD与AE是对应边,已知:∠A=43°,
∠B=30°,求∠ADC的大小.
课堂检测
1.全等用符号 表示,读作: .
2.若△BCE≌△CBF,则∠CBE= , ∠BEC= ,BE= , CE= .
3.判断题
1)全等三角形的对应边相等,对应角相等.( )
2)全等三角形的周长相等,面积也相等. ( )
3)面积相等的三角形是全等三角形. ( )
4)周长相等的三角形是全等三角形. ( )
4.如图:△ABC≌△DBF,找出图中的对应边,对应角.
答:∠B的对应角是 ,∠C的对应角是 ,
∠BAC的对应角是 ;
AB的对应边是 ,AC的对应边是 ,
BC的对应边是 .
课后作业:课本P4习题第1、2题
板书设计:
11.1 全等三角形
一、全等形、全等三角形的概念
二、全等三角形的对应元素及表示
三、全等三角形的性质
教学反思:
11.2.1三角形全等的判定
学习目标
1.理解三边对应相等的两个三角形全等的内容.
2.会运用“边边边”条件证明两个三角形全等.
3. 会作一个角等于已知角.
自主学习
一、课前准备
1. 叫做全等三角形
2.全等三角形的 和 相等
3.将△ABC沿直线BC平移,得到△DEF,说出你得到的结论,说明理由?
如果AB=5, ∠A=55°, ∠B=45°,那么DE= ,∠F= .
二、自主探究
自主探究三角形全等的条件:
阅读课本P6探究2之前,回答下面问题:
通过探究
(1)只给一个条件对应相等的两个三角形一定全等吗?
①只给一条边时;
②只给一个角时;
(2)如果给出两个条件画三角形,你能说出有哪几种可能的情况?
①给出两个角时;
②给出两条边时;
③给出一条边和一个角时;
(3)由上面的几种情景,两个三角形满足一个或两个条件时,它们一定全等吗?
(4)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况?
①我们先来探究两个三角形三个角相等的情况:
②画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?
③上面的探究反映了什么规律?
阅读课本P6-7探究2至例1前,回答下面问题:
的两个三角形全等,简写为“ ”或“ ”.
三、例题学习
阅读课本P7例1,学习“边边边”证明两个三角形全等的格式.
巩固练习
1. 如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC(2)∠B=∠D
证明:
(1)在△ABC和△ADC中
(公共边)
∴△ABC≌△ADC( )
(2)∵△ABC≌△ADC
∴∠B=∠D( )
2.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
证明:
四、作一个角等于已知角
阅读课本P7最后一段至P8,回答书中问题.
课堂小结
本节课你有哪些收获?
课堂检测
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
证明:
课后作业:课本P15习题第1、2题
板书设计:
11.2.1 三角形全等的条件(一)
一、三角形全等的条件
三边对应相等的两三角形全等(SSS)
二、例题
三、作一个角等于已知角
教学反思:
11.2.2全等三角形的识别(二)(SAS)
学习目标:会运用“边角边”公理证明三角形全等的简单问题
重难点:1、会运用“边角边”公理证明三角形全等的简单问题
2、分清用两边一角证明三角形相似和全等的不同。
自学过程:
知识回顾:
一、判别三角形相似的方法之二:
1、如果两个三角形有 _____边对应______,并且____相等,那么这两个三角形相似.
新课讲解:
做一做 以图24.2.5中的两条线段和一个角画一个三角形,使该角恰为这两条线段的夹角.
步骤:
画一线段AB使它的长度等于4cm.
以点A为顶点,作∠BAP=45°,在射线AP上截取AC=3cm,
连结BC.△ABC即为所求.
把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?
换两条线段和一个角,用同样的方法试试,是否有同样的结论.
A C
A B
A
这样我们就得到识别三角形全等的另一种简便的方法
如果两个三角形有 _____边及其______分别对应____,那么这两个三角形全等.简记为(S.A.S.).
对比判别三角形相似的方法
如果两个三角形有 _____边对应______,并且____相等,那么这两个三角形相似.
例2 如图11-1,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
做一做 如图24.2.7,已知两条线段和一个角,以这两条线段为边,以这个角为其中一条边的对角,画一个三角形.
图24.2.7
把你画的三角形与其他同学画的三角形进行比较,所有的三角形一定都会全等吗?
练 习
根据题目条件,判断下面的三角形是否全等?
(3) (4)
点M是等腰梯形ABCD底边AB的中点,△AMD和△BMC全等吗?试说明你的理由?
综合练习:
填空:
如图11-2,AB=AD,AC=AE,
则可得△ABC≌____
其理由是______
2、如图(1):OA=OD,OB=OC,求证:△ABO≌△DCO
证明: OA=OD OB=OC( )
____=_____( )
△ABO≌△DCO( )
3、如图(2):已知AB=DC,∠ABC=∠DCB,求证:AC=BD
证明:AB=DC,∠ABC=∠DCB ( )
BC=________( )
△BCD≌_______,( )
AC=________( )
如图(1) 如图(2)
选择:
1、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是( )
A ∠A B ∠B C ∠C D ∠B或∠D
l
2、如图:直线l是四边形ABCD的对称轴,如果,有下列 A
结论:(1)AB∥DC(2)AB=BC(3)ABBC(4) AO=OC, B O D
其中正确的结论有( )
A 1个 B 2个 C 3个 D 4个 C
3、具有下列条件的两个等腰三角形,不能判定它们全等的是( )
A 顶角、一腰对应相等 B 底边、一腰对就相等
C 两腰对应相等 D 一腰、一底角、一底边对应相等
△ABC和△A′B′C′边角条件如图:那么这两个三角形( ) C′
A全等 B不全等
C不一定全等 D相似
证明:1、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?
2、已知:AD=BC,∠ADC=∠BCD.求证: ∠BDC=∠ACD.
3、如图,AE=DB,BC=EF,BC∥EF,说明△ABC和△DEF全等的理由.
4、如图:点M是等腰梯形ABCD底边AB上的中点,则MD与MC的大小有何关系,试说明理由。
5、已知点A、B、C、D在同一条直线上,AB=CD, ∠D=∠ECA,试问:AE与BF的大小关系,并说明理由。
6、如图:在△ABC中,AB=AC, ∠BAC=90°,在AB上取点P,边CA的延长线上取点Q,使AP=AQ,边CP与BQ交于点S,求证:△CAP≌△BAQ
7、如图,AB=AD,AC=AE,∠BAE=∠DAC, △ABC与△ADE全等吗?并说明理由。
11.2.3 全等三角形的识别(三)(ASA及AAS)
学习目标:会运用“角边角”公理及其推论证明三角形全等的简单问题
重难点:能灵活运用“角边角”公理及其推论证明三角形全等的简单问题
自学过程:
做一做 如图24.2.9,已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.
步骤:
一线段AB使它的长度等于4cm.
分别以点A、B为顶点,作∠BAP=40°∠ABQ=60°,AP、BQ相交于点C,
△ABC即为所求.
把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
换两个角和一条线段, 用同样的方法试试看,是否有同样的结论.
A
B
A B
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的_______及其____分别对应_____,那么这两个三角形全等.简记为(A.S.A.).
例3 如图所示,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC≌△DCB.
解 ∠ABC=∠DCB,∠ACB=∠DBC,
BC是______,
______( )
思 考
如图24.2.11,如果两个三角形有两个角及其中一个角的对边分别对应相等,
那么这两个三角形是否一定全等?
图24.2.11
你的结论是______________________________________
证明: ∠A=∠D,∠C=∠F,
∠B=180°-______,∠E=180°-____,
∠____=∠______
又∠___=∠___,AB=____
△ABC≌△DEF.( )
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的_______及其____分别对应_____,那么这两个三角形全等.简记为(A.A.S.).
小结: 如果知道两个三角形的两个角及一条边分别对应相等,这时应该有两种不同的情况: 一种情况是两个角及两角的____(ASA); 另一种情况是两个角及其中一角的___(AAS),两种情况都可以证明三角形全等。如图24.2.8所示.
图24.2.8
练 习
填空:
1、如图:D是△ABC的边AB上一点,DE交AC于点E,交CF于点 F,DE=FE,FC∥AB, 求证:AE=CE
证明: FC∥AB( ) ∴∠_____=∠_____,
∠_____=∠_____, 又 DE=FE( )
∴△AED≌____( )
∴AE=CE( )
2、如图:点B、F、C、E在同一条直线上,FB=CE,
AB∥ED,AC∥FD,求证:AB=DE
证明: FB=CE( )
FB+___=CE+__( )
即:____=____
AB∥ED,AC∥FD
∠ABC=∠_______,∠ACB=∠_______
△ABD≌________,( )
AB=DE,( )
3、如图:AB=CD,AD=BC,EF过BD的中点O,求证:△OBF≌△ODE
证明:AB=CD,AD=BC( )
_________=__________( )
△ABD≌________,( )
∠CBD=_______
EF过BD的中点O( )
______=__________
又∠FOB=∠_____( )
△OBF≌_______( )
选择
1、下列说法中,正确的是( )
A所有的等腰三角形全等 B有两边对应相等的两个等腰三角形全等
C有一边对应相等的两个等腰三角形全等 D腰和顶角对应相等的两个等腰三角形全等
2、在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A 一定不全等 B 一定全等 C 不一定全等 D 以上都不对
3、如图:点E在△ABC外部,点D在BC边上,DE
交AC于F,若∠1=∠2=∠3,AC=AE,则( )
A △ABD≌△AFD B △AFE≌△ADC
C △AFE≌△DFC D △ABC≌△ADE
4、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )
A(1) (2) (3) B (1) (2) (5) C (1) (3) (5) D(2) (5) (6)
三、证明与计算:
根据题目条件,判别下面的两个三角形是否全等,并说明理由.
△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.
3、如图,AB=DE,AC∥DF,BC∥EF,△ABC与△DEF全等吗?试说明理由.
4、如图,∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?试说明理由。
5、已知: 如图,∠C=∠D,CE=DE.求证: ∠DAB=∠ABC.
6、已知: 如图,∠BDA=∠CEA,AE=AD.求证: AB=AC.
7、已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC, ∠B=∠C,求证:BD=CE
11.2.4 全等三角形的识别(四)(HL)
学习目标:会运用“斜边、直角边公理” 证明三角形全等的简单问题
重难点:
1、会运用“斜边、直角边公理”(HL) 证明三角形全等的简单问题
2、了解SSS、SAS、ASA、AAS也适用于直角三角形。
自学过程:
知识回顾:
一、判别三角形相似的方法之三:
如果一个三角形的_______分别与另一个三角形的_______对应相等,那么这两个三角形相似.
我们知道,对于两个三角形,有“边、边、角”对应相等,是不能保证它们全等的.但是,在两个直角三角形中,当斜边及一条直角边分别对应相等时,也具有“边、边、角”对应相等的条件,这时这两个直角三角形是否全等呢?
做一做 试以24.2.12中的两条线段AC、AB分别为直角边和斜边画一个直角三角形.
步骤:
画∠MCN=90°,
在射线CM上截取AC的长度,
以点A为圆心,以线段AB的长为半径画圆弧,交射线CN于点B,
连结AB,△ABC即为所求.
把你画的图形与周围的同学画的比较一下,所画的图形都全等吗?请按照下题的步骤证明你的结论。
如图,AC=DF,AB=DE,∠C=∠F=90°,试说明△ABC≌△DEF.
∠C=∠F=90°
BC=_________,EF=____________(勾股定理)
又 AC=DF,AB=DE,
_____=____
又∠__=∠__,AC=____
△ABC≌△DEF.( )
由此可以得到如下结论:
如果两个直角三角形的_____及一条______分别对应相等,那么这两个直角三角形全等. 称为斜边、直角边公理,简记为(H.L.).
注意:
1、斜边、直角边公理(HL)只能用于证明直角三角形的全等,对于其它三角形不适用。
2、SSS、SAS、ASA、AAS适用于任何三角形,包括直角三角形。
例4 如图24.2.13,AB是圆O的直径,AC=AD,试说
明△ABC和△ABD全等.
解 AB为⊙O的直径
∠ACB=∠___=__°.
又AC=AD,___=___,
△ABC≌△ABD.( )
练 习
如图,AC=AD,∠C=∠D=90°,试说明BC与BD相等.
以下面格点图中的格点为顶点,画出所有的直角三角形,并说明哪些直角三角形是全等的.
(第2题)
综合练习:
一、填空:
两条直角边对应相等的两个直角三角形______,理由是________
有一条边和一个锐角对应相等的两个直角三角形_____,理由是______
如图(1):BA⊥AC,CD∥AB,AB=CE,BC=DE,则△CDE≌______,
理由是_____,且有∠ACB=________,∠ABC=_______,
由此可知BC与DE互相__________
如图:AD、A′D′分别是锐角△ABC和△A′B′C′
中BC,B′C′边上的高,且AB=A′B′,AD=A′D′,若
使△ABC≌△A′B′C′,需补充条件是______
(只需填写一个你认为适当的条件)
二、选择:
1、两个直角三角形全等的条件是( )
A一锐角对应相等B两锐角对应相等C一条边对应相等D两条边对应相等
2、判断下列命题:(1)在Rt△ABC中,两锐角互余(2)有两个锐角不互余的三角形不是直角三角形(3)一条直角边对应相等的两个直角三角形全等(4)有两个锐角对应相等的两个直角三角形全等,其中正确的有( )
A 1个 B 2个 C 3个 D 4个
3、下列说法正确的有( )
(1)两条直角边对应相等的两个直角三角形全等(2)一条边和一个锐角对应相等的两个直角三角形全等(3)两条边对应相等的两个直角三角形全等(4)两个锐角对应相等的两个直角三角形全等。
A 1个 B 2个 C 3个 D 4个
4、在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=A′B′,那么下列结论中正确的是( )
A AC=A′C′ B BC=B′C′ C AC=B′C′ D ∠A=∠A′
下列叙述的图形中,是全等三角形的只有(
A 两个含60°角的直角三角形 B 腰对应相等的两个等腰三角形
C 有一边相等的两个等边三角形 D 面积相等的两个直角三角形
6、如图:△ABC中,∠C=90°,AC=BC,AD平分∠CAB,
交BC于D点,DE⊥AB于点E,且AB=60cm,则△BED的
周长为( )
A 100cm B 80cm C 60cm D 40cm
证明:
1、如图:CE⊥AB,DF⊥AB,垂足分别为EF,AC∥DB,且AC=BD,求证:CE=DF
2、如图:△ABC是等腰三角形,AB=AC,AD是高,
求证(1)BD=DC(2)∠BAD=∠CAD
3、如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,求证(1)AE=CF(2)AB∥CD
4、如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足为E、F,求证:EB=FC
5、如图:在Rt△ABC和Rt△A′B′C′中,∠ACB=∠A′C′B′=90°,CDAB,C′D′A′B′,且CD=C′D′,BC=B′C′,求证:Rt△ABC≌Rt△A′B′C′
11.3角平分线的性质
自学目标 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网" \t "_blank ):
(1)掌握角平分线的性质定理;
(2)能够运用性质定理证明两条线段相等;
(3)角平分线的性质定理及它的应用。
重难点 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网" \t "_blank ):角平分线的性质定理及它的应用。
自学过程:
一、复习:
1、判断两个三角形全等的方法:
(1)三边分别相等的两个三角形全等。
(2)有两边级其夹角对应相等的两个三角形全等。
(3)有两角及其夹边对应相等的两个三角形全等。
(4)有两个角及其中一角的对边对应相等的两个三角形全等。
(5)有一条直角边和斜边对应相等的两个直角三角形全等。
2、练习:根据题目的结论,添加相应的条件。
(1)如上图,AB=DE,AC=DF,______=_______,那么根据(SSS)可得
(2)如上图,AB=DE,AC=DF,______=_______,那么根据(SAS)可得
(3)如上图,AB=DE,______=______,______=_______,那么根据(ASA)可得
(4)如上图,AB=DE,______=______,_______=_______,那么根据(AAS)可得
(5)如右图,,_____=_____,
_______=_______,那么根据(HL)
可得
三、“角平分线上的点到这个角两边的距离相等”
请你自己设计出一条几何证明题,去证明上面的命题是否正确:
小光已经做出了一些步骤,请你帮他补充完整:
解: 如右图:
已知:__________________,
___________________
求证:______=_______
证明:
归纳:从上面的我们可知道“角平分线上的点到这个角两边的距离相等”这是一个_________(填“真”或“假”)命题。
练习:根据上面定理完成书本P21 思考。
四:把前面的定理反过来可得:“角的内部到角两边的距离相等的点在角的平分线上”
请你自己设计出一条几何证明题,去证明上面的命题是否正确:
小白已经做出了一些步骤,请你帮他补充完整:
解:如右图,过______做射线
已知:,;
并且_______=_______
求证:_____是的平分线
证明:
归纳:从上面的我们可知道“角的内部到角两边的距离相等的点在角的平分线上”这是一个_________(填“真”或“假”)命题。
五、练习:
A组:
1、请你利用尺规作图,画出的平分线
B组:
书P22页习题11.3第1----5题。(可做在书本上)
C组:请你利用尺规作图在内部找一个点,
使这个点到三边距离相等
3㎝
3㎝
3cm
45
45
45
300
700
800
300
800
700
A
B
C
D
B
C
D
A
PAGE
