人教版八年级上册 数学 课件: 12.2 三角形全等的判定(16张)
文档属性
| 名称 | 人教版八年级上册 数学 课件: 12.2 三角形全等的判定(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 262.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 11:25:35 | ||
图片预览

文档简介
12.2 三角形全等的判定
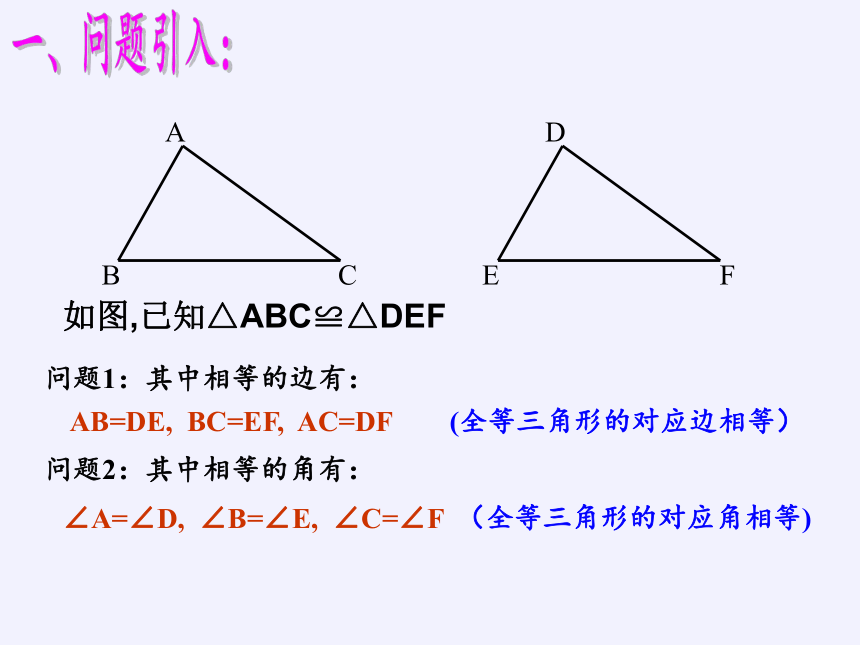
一、问题引入:
问题1:其中相等的边有:
问题2:其中相等的角有:
AB=DE, BC=EF, AC=DF
∠A=∠D, ∠B=∠E, ∠C=∠F
如图,已知△ABC≌△DEF
A
B
C
D
E
F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
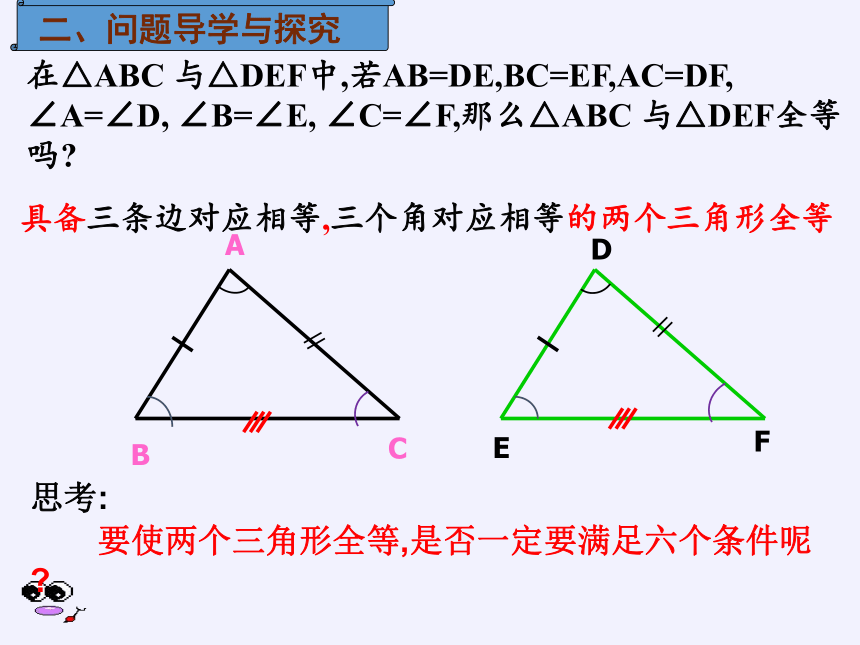
在△ABC 与△DEF中,若AB=DE,BC=EF,AC=DF,
∠A=∠D, ∠B=∠E, ∠C=∠F,那么△ABC 与△DEF全等吗?
具备三条边对应相等,三个角对应相等的两个三角形全等
A
B
C
D
E
F
思考:
要使两个三角形全等,是否一定要满足六个条件呢?
二、问题导学与探究
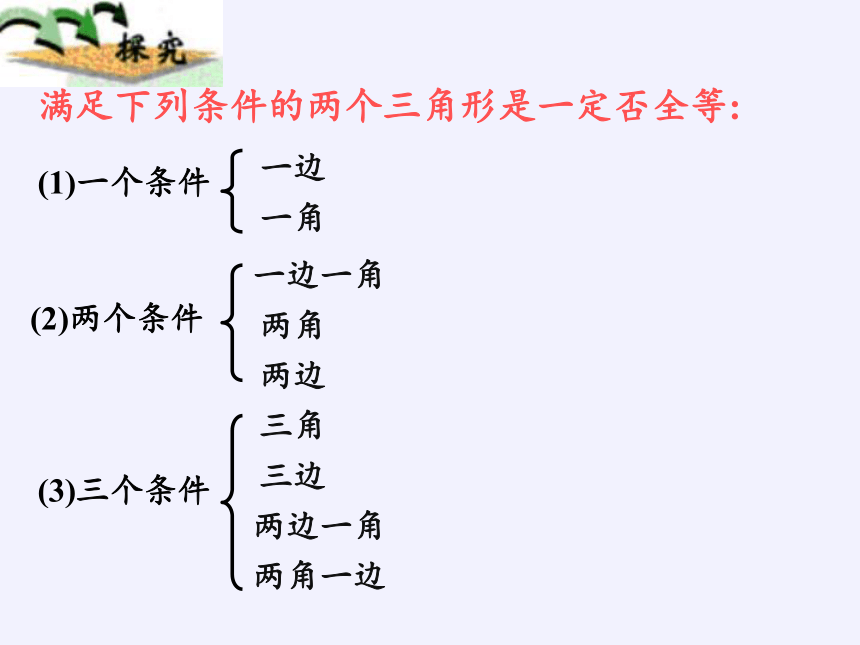
(1)一个条件
(2)两个条件
(3)三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
满足下列条件的两个三角形是一定否全等:
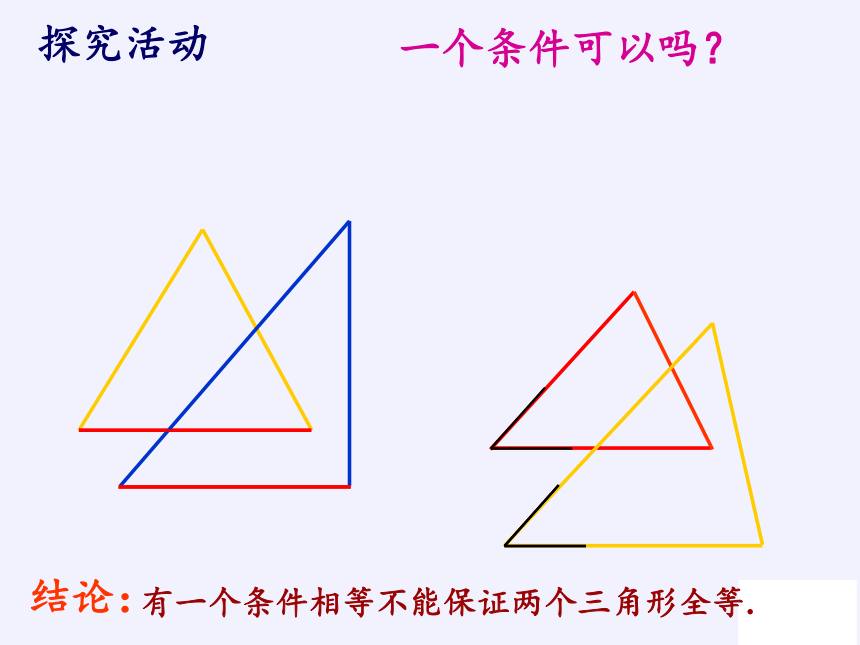
一个条件可以吗?
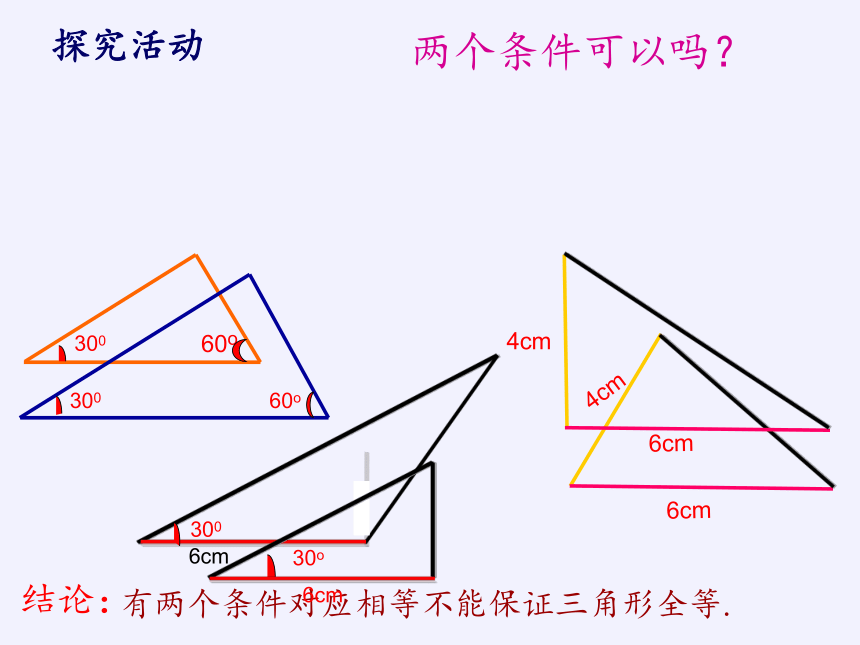
探究活动
结论:
有一个条件相等不能保证两个三角形全等.
6cm
300
有两个条件对应相等不能保证三角形全等.
60o
300
两个条件可以吗?
4cm
6cm
300
60o
4cm
6cm
30o
6cm
结论:
探究活动
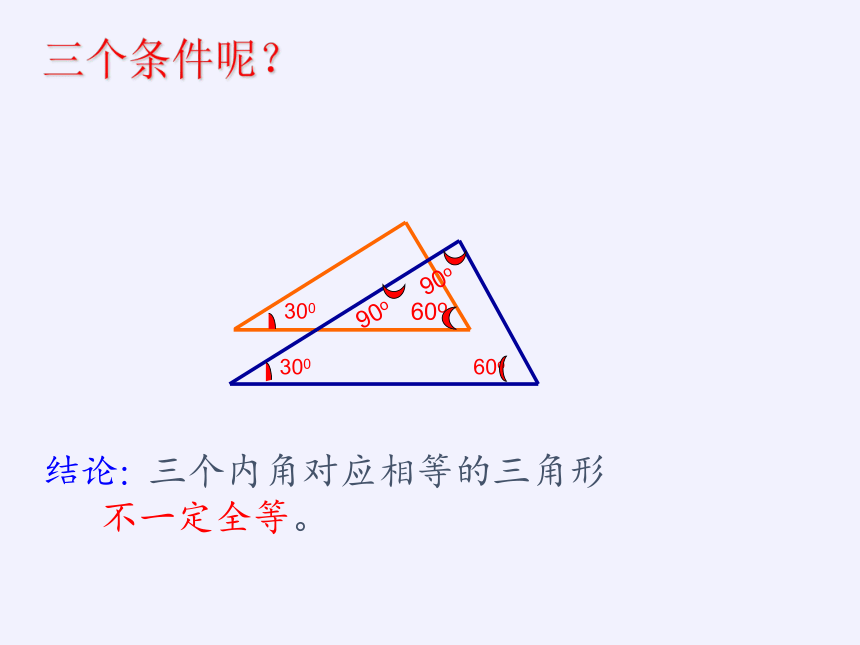
结论: 三个内角对应相等的三角形
不一定全等。
60o
300
300
60o
90o
90o
三个条件呢?
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
×
×
×
×
(1)一个条件
(2)两个条件
(3)三个条件
三边相等的两个三角形会全等吗?
画法:
动手试一试
探究活动
你能得出什么结论?
满足下列条件的两个三角形是否一定全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
×
×
×
×
√
A
B
C
A
B
C
三边对应相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢?
≌
结论
∴ ∠A = ∠___
∠B = ∠___
∠C = ∠___
应用
说说木条钉成的三角形框架与四边形框架有什么不同?
填一填:
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
BF=CD
或 BD=CF
三、问题解读与达标检测:
(1) 已知:如图,AB=AD,BC=CD,求证:△ABC≌ △ADC
A
B
C
D
证明:在△ABC和△ADC中
AB=AD ( )
BC=CD ( )
AC
=
( )
AC
已知
已知
公共边
∴ △ABC ≌ △ADC( )
SSS
例1:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点 D的支架.
求证: △ABD≌△ACD.
A
B
C
D
A
B
C
D
.
(1)
(2)∠B = ∠C.
(3)AD⊥BC
(4)AD是△ABC的角平分线
谢 谢
一、问题引入:
问题1:其中相等的边有:
问题2:其中相等的角有:
AB=DE, BC=EF, AC=DF
∠A=∠D, ∠B=∠E, ∠C=∠F
如图,已知△ABC≌△DEF
A
B
C
D
E
F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
在△ABC 与△DEF中,若AB=DE,BC=EF,AC=DF,
∠A=∠D, ∠B=∠E, ∠C=∠F,那么△ABC 与△DEF全等吗?
具备三条边对应相等,三个角对应相等的两个三角形全等
A
B
C
D
E
F
思考:
要使两个三角形全等,是否一定要满足六个条件呢?
二、问题导学与探究
(1)一个条件
(2)两个条件
(3)三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
满足下列条件的两个三角形是一定否全等:
一个条件可以吗?
探究活动
结论:
有一个条件相等不能保证两个三角形全等.
6cm
300
有两个条件对应相等不能保证三角形全等.
60o
300
两个条件可以吗?
4cm
6cm
300
60o
4cm
6cm
30o
6cm
结论:
探究活动
结论: 三个内角对应相等的三角形
不一定全等。
60o
300
300
60o
90o
90o
三个条件呢?
满足下列条件的两个三角形是一定否全等:
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
×
×
×
×
(1)一个条件
(2)两个条件
(3)三个条件
三边相等的两个三角形会全等吗?
画法:
动手试一试
探究活动
你能得出什么结论?
满足下列条件的两个三角形是否一定全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
×
×
×
×
√
A
B
C
A
B
C
三边对应相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢?
≌
结论
∴ ∠A = ∠___
∠B = ∠___
∠C = ∠___
应用
说说木条钉成的三角形框架与四边形框架有什么不同?
填一填:
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
BF=CD
或 BD=CF
三、问题解读与达标检测:
(1) 已知:如图,AB=AD,BC=CD,求证:△ABC≌ △ADC
A
B
C
D
证明:在△ABC和△ADC中
AB=AD ( )
BC=CD ( )
AC
=
( )
AC
已知
已知
公共边
∴ △ABC ≌ △ADC( )
SSS
例1:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点 D的支架.
求证: △ABD≌△ACD.
A
B
C
D
A
B
C
D
.
(1)
(2)∠B = ∠C.
(3)AD⊥BC
(4)AD是△ABC的角平分线
谢 谢
