人教版八年级上册数学 12.3 角的平分线的性质课件(15张PPT)
文档属性
| 名称 | 人教版八年级上册数学 12.3 角的平分线的性质课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 154.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 20:26:00 | ||
图片预览


文档简介
12.3 角的平分线的性质
1.角平分线的概念
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线
复习提问
问题1 在练习本上画一个角,怎样得到这个角的平分线?
用量角器度量,也可用折纸的方法.
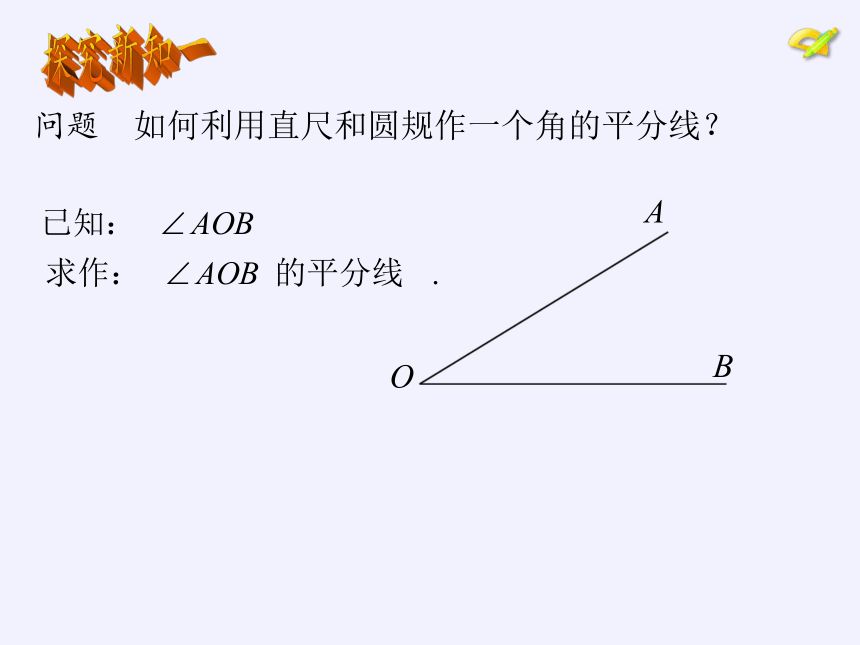
问题 如何利用直尺和圆规作一个角的平分线?
A
B
O
探究新知一
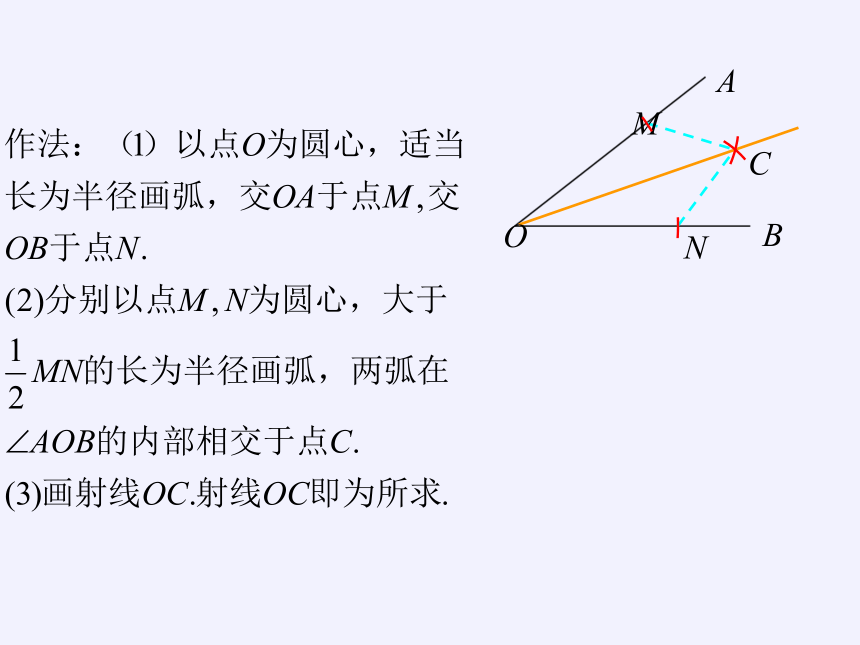
A
B
O
M
N
C
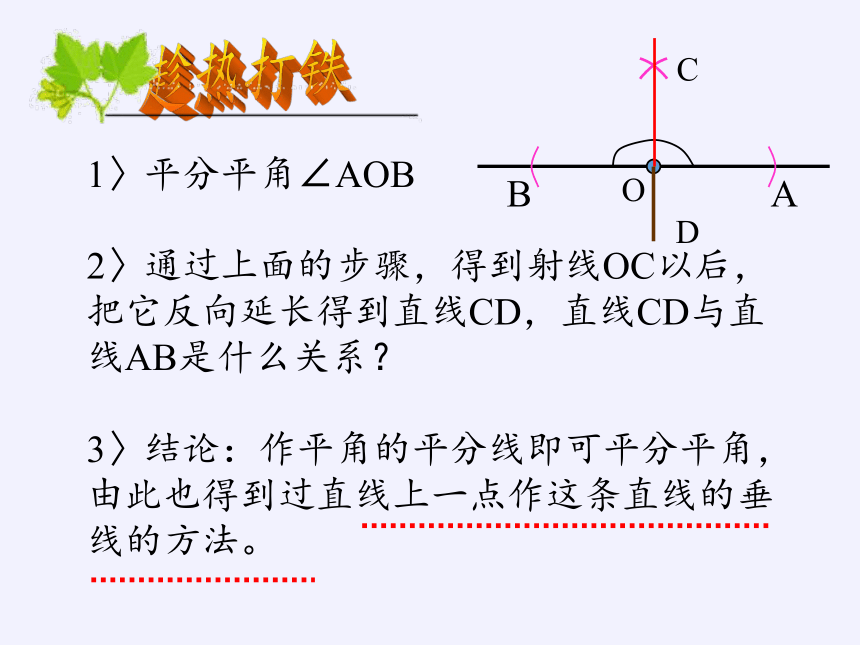
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
趁热打铁
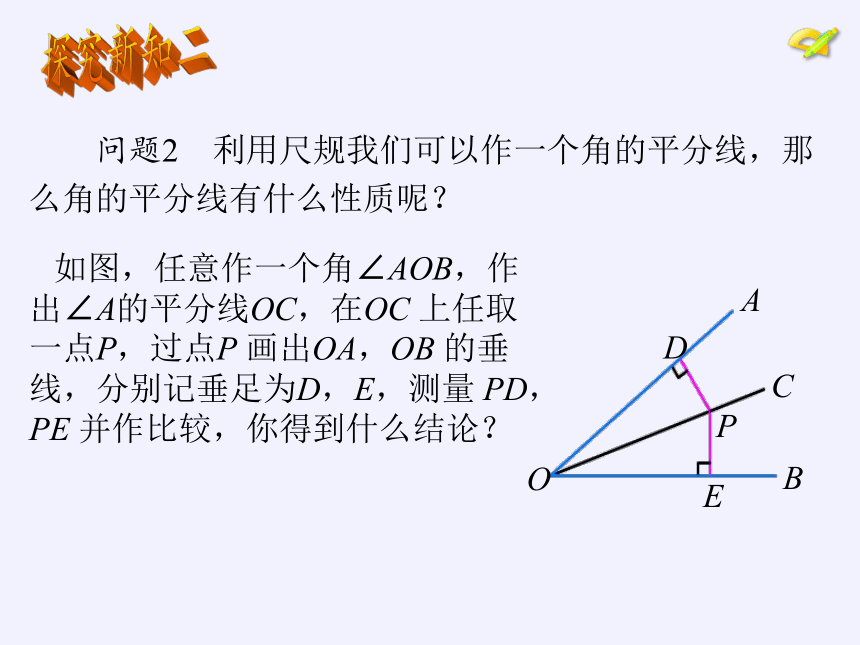
如图,任意作一个角∠AOB,作出∠A的平分线OC,在OC 上任取一点P,过点P 画出OA,OB 的垂线,分别记垂足为D,E,测量 PD,PE 并作比较,你得到什么结论?
问题2 利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
A
B
O
P
C
D
E
探究新知二
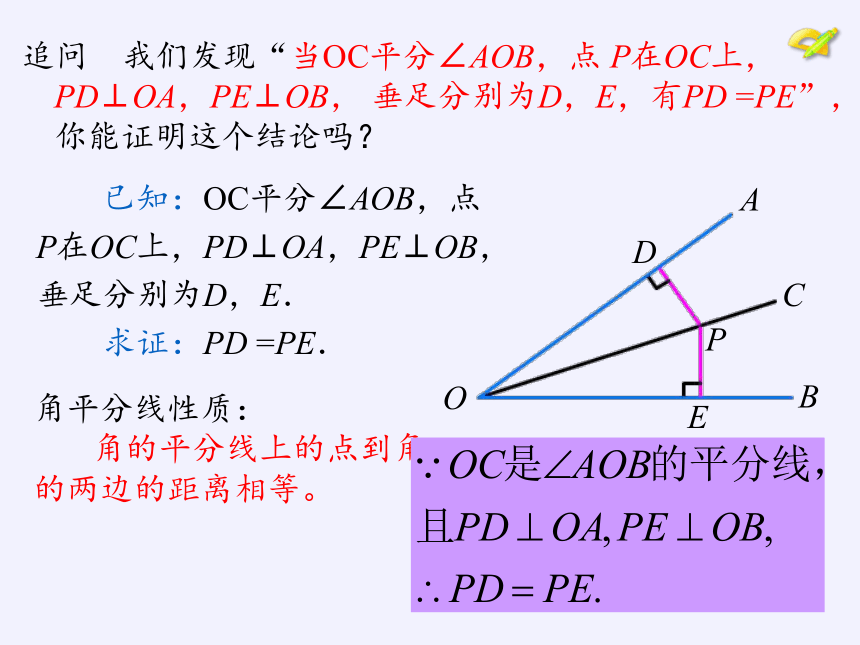
已知:OC平分∠AOB,点
P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD =PE.
追问 我们发现“当OC平分∠AOB,点 P在OC上,PD⊥OA,PE⊥OB, 垂足分别为D,E,有PD =PE”,你能证明这个结论吗?
A
B
O
P
C
D
E
角平分线性质:
角的平分线上的点到角的两边的距离相等。
例1:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为?
A
C
D
B
E
例题讲解
E
例2:如图,△ABC的角平分线BM、CN相交于点P。求证:点P到三角形三边的距离均相等。
A
B
C
P
E
F
G
M
N
例题讲解
练习1 下列结论一定成立的是 .
(1)如图,OC 平分∠AOB,点P 在OC 上,D,E 分
别为OA,OB 上的点,则PD =PE.
A
B
O
P
C
D
E
(2)如图,点P 在OC 上,PD⊥OA,PE⊥OB,垂足
分别为D,E,则PD =PE.
(3)如图,OC 平分∠AOB,点P 在OC 上,PD⊥OA,
垂足为D.若PD =3,则点P 到OB 的距离为3.
(3)
巩固练习
A
B
C
D
E
F
练习2 如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,
则PE=___cm.
A
D
O
B
E
P
C
练习3 如图,△ABC中,∠B =∠C,AD 是∠BAC
的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.求证:EB =FC.
练习4 如图,AE∥CF,AG、CG分别平分∠EAC和∠FCA,过点G的直线BD⊥AE,交AE于B,交CF于D,求证:AB+CD=AC.
?????????????????????????????????
(1)本节课学习了哪些主要内容?
(3)角的平分线的性质为我们提供了证明什么的方法? 在应用这一性质时要注意哪些问题?
课堂小结
教科书习题12.3第4、5题.
布置作业
谢 谢
1.角平分线的概念
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线
复习提问
问题1 在练习本上画一个角,怎样得到这个角的平分线?
用量角器度量,也可用折纸的方法.
问题 如何利用直尺和圆规作一个角的平分线?
A
B
O
探究新知一
A
B
O
M
N
C
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
趁热打铁
如图,任意作一个角∠AOB,作出∠A的平分线OC,在OC 上任取一点P,过点P 画出OA,OB 的垂线,分别记垂足为D,E,测量 PD,PE 并作比较,你得到什么结论?
问题2 利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
A
B
O
P
C
D
E
探究新知二
已知:OC平分∠AOB,点
P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD =PE.
追问 我们发现“当OC平分∠AOB,点 P在OC上,PD⊥OA,PE⊥OB, 垂足分别为D,E,有PD =PE”,你能证明这个结论吗?
A
B
O
P
C
D
E
角平分线性质:
角的平分线上的点到角的两边的距离相等。
例1:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为?
A
C
D
B
E
例题讲解
E
例2:如图,△ABC的角平分线BM、CN相交于点P。求证:点P到三角形三边的距离均相等。
A
B
C
P
E
F
G
M
N
例题讲解
练习1 下列结论一定成立的是 .
(1)如图,OC 平分∠AOB,点P 在OC 上,D,E 分
别为OA,OB 上的点,则PD =PE.
A
B
O
P
C
D
E
(2)如图,点P 在OC 上,PD⊥OA,PE⊥OB,垂足
分别为D,E,则PD =PE.
(3)如图,OC 平分∠AOB,点P 在OC 上,PD⊥OA,
垂足为D.若PD =3,则点P 到OB 的距离为3.
(3)
巩固练习
A
B
C
D
E
F
练习2 如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,
则PE=___cm.
A
D
O
B
E
P
C
练习3 如图,△ABC中,∠B =∠C,AD 是∠BAC
的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.求证:EB =FC.
练习4 如图,AE∥CF,AG、CG分别平分∠EAC和∠FCA,过点G的直线BD⊥AE,交AE于B,交CF于D,求证:AB+CD=AC.
?????????????????????????????????
(1)本节课学习了哪些主要内容?
(3)角的平分线的性质为我们提供了证明什么的方法? 在应用这一性质时要注意哪些问题?
课堂小结
教科书习题12.3第4、5题.
布置作业
谢 谢
