人教版九年级上册 数学 课件: 25.1.2 概率(33张)
文档属性
| 名称 | 人教版九年级上册 数学 课件: 25.1.2 概率(33张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 951.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 10:43:32 | ||
图片预览











文档简介
概率
温故知新
必然事件:
在一定条件下必然发生的事件.
不可能事件:
在一定条件下不可能发生的事件.
随机事件:
在一定条件下可能发生也可能不发生的事件.
练 一 练
下面的一些事件是什么事件?
(1)度量三角形的内角和,结果360°
(2)“抛一块石头,下落”;
(3)明天会下雨;
(4)“某人射击一次,中靶”;
(5)“掷一枚硬币,出现正面”。
实验1:掷一枚硬币,落地后:
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
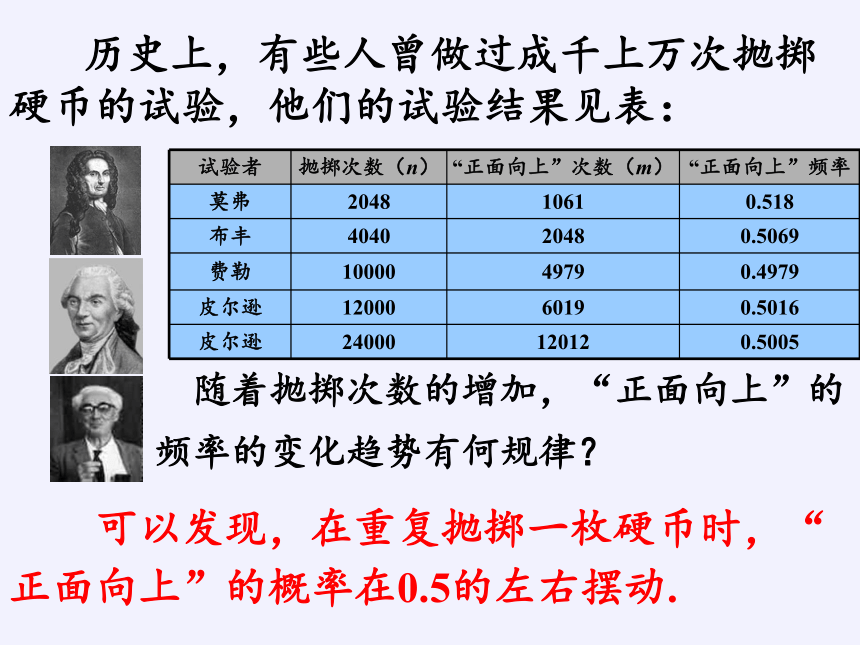
历史上,有些人曾做过成千上万次抛掷硬币的试验,他们的试验结果见表:
试验者
抛掷次数(n)
“正面向上”次数(m)
“正面向上”频率
莫弗
2048
1061
0.518
布丰
4040
2048
0.5069
费勒
10000
4979
0.4979
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
可以发现,在重复抛掷一枚硬币时,“正面向上”的概率在0.5的左右摆动.
随着抛掷次数的增加,“正面向上”的
频率的变化趋势有何规律?
一般地,对于随机事件A,我们把刻画其发生可能性大小的数值,称为事件A的概率。
记为P(A).
概率描述了事件发生可能性的大小
需要注意,概率是针对大量试验而言的,大量试验反映的规律,并非在每次试验中一定存在。
“抛掷一枚硬币50次,则“正面向上”的次数必为25次.”这句话对吗?
概率是针对大量试验而言的,大量试验反映的规律,并非在每次试验中一定存在.
某人连掷硬币50次,结果只有10次正面向上,这种情况完全正常?
这件事并不奇怪,因为预报的降水概率是根据大量统计记录得出的,是符合大多数同等条件协定的实际情况的,某些例外情况是可能发生的.
某气象台报告:今年11月11日有大雨,可这天并没下雨,所以天气预报不可信?
实验2:抛掷一个质地均匀的骰子
(1)它落地时,向上的点数有几种可能的结果?
(2)各点数出现的可能性,会相等吗?
(3)试猜想:你能用一个数值,来说明各点数
出现的可能性大小吗?
正方体有六个面,6种结果。
相等
实验3: 从分别标有1,2,3,4,5的
五根纸签中随机抽取一根
(1)抽取的结果会出现几种可能?
(2)每根纸签抽到的可能性会相等吗?
(3)试猜想:你能用一个数值来说明每根纸签
被抽到的可能性大小吗?
实验3:从分别标有1,2,3,4,5的五根
纸签中随机抽取一根
(4) 你能用一个数值来说明抽到标有1的
可能性大小吗?
(5) 你能用一个数值来说明抽到标有偶数号
的可能性大小吗?
抽出的签上号码有5种可能,即1,2,3,4,5。
标有1的只是其中的一种,所以标有1的概率就为
抽出的签上号码有5种可能,即1,2,3,4,5。标有偶数号的有2,4两种可能,所以标有偶数号的概率就为
摸到红球的概率
学有所用
3
4
摸出一球所有可能出现
的结果数
摸到红球可能出现的结果数
摸到红球的概率
P(摸到红球)=
盒子中装有3个黑棋子和2个白棋子(只有颜色不同,其它均相同),从中摸出一棋子,是黑棋的可能性是多少?
P(摸到黑棋子)=
分析:“从下面的一堆牌中,任意抽一张,抽到红牌”这一事件是什么事件,能不能求出概率?
必然事件
P(抽到红牌)=
分析:“从下面的一堆牌中,任意抽一张,抽到红牌”这一事件是什么事件,能不能求出概率?
不可能事件
P(抽到红牌)=
分析:“从下面的8张牌中,任意抽一张,抽到红牌”这一事件是什么事件,能不能求出概率?
随机事件
P(抽到红牌)=
归纳总结
掷一个骰子,观察向上的一面的 点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5。
试 一试 飞的更高
袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则:
P(摸到红球)= ;
P(摸到白球)= ;
P(摸到黄球)= ;
如图:是一个转盘,转盘分成7个相同的扇形,颜色分为红、黄、绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时,当作指向右边的扇形)求下列事件的概率:
(1)指向红色;
(2)指向红色或黄色;
(3)不指向红色.
解:按颜色共有7种等可能性的结果,分别记
为:红1,红2,红3,绿1,绿2,黄1,黄2.
(1)指针指向红色(记为事件A)的
结果有3个,即红1,红2,红3,则
P(A)=
解:按颜色共有7种等可能性的结果,分别记
为:红1,红2,红3,绿1,绿2,黄1,黄2.
(2)指针指向红色或黄色(记为事件B)
的结果共有5个
即红1,红2,红3 ,黄1,黄2 ,则
P(B)=
解:按颜色共有7种等可能性的结果,分别记
为:红1,红2,红3,绿1,绿2,黄1,黄2.
(3)指针不指向红色(记为事件C)的
结果共有4个
即绿1,绿2,黄1,黄2 ,则
P(C)=
计算机扫雷游戏,在9×9个小方格中,随机埋藏着10个地雷,每个小方格只有1个地雷,,小王开始随机踩一个小方格,标号为3,在3的周围的正方形中有3个地雷,我们把他的区域记为A区,A区外记为B区,下一步小王应该踩在A区还是B区?
如图:计算机扫雷游戏,在9×9个小方格中,随机埋藏着10个地雷,每个小方格只有1个地雷,,小王开始随机踩一个小方格,标号为3,在3的周围的正方形中有3个地雷,我们把他的去域记为A区,A区外记为B区,,下一步小王应该踩在A区还是B区?
由于3/8大于7/72,
所以第二步应踩B区
解:A区有8格3个雷,遇到地雷的概率为3/8,
B区有9×9-9=72个小方格,
还有10-3=7个地雷,
遇到地雷的概率为7/72,
甲、乙 两人做如下的游戏:
你认为这个游戏对甲、乙双方公平吗?
任意掷出骰子后,若朝上的数字是6,则甲获胜;
若朝上的数字不是6,则乙获胜。
解:∵P(甲获胜) = P(乙获胜) =
∴P(乙获胜) > P(甲获胜)
∴ 游戏对甲、乙双方不公平
话说唐僧师徒越过狮驼岭,吃完午饭后,三徒弟商量着今天由谁来刷碗,可半天也没个好主意。还是悟空聪明,他灵机一动,扒根猴毛一吹,变成一粒骰子,对八戒说道:我们三人来掷骰子:
如果掷到 2的倍数就由八戒来刷碗;
如果掷到 3的倍数就由沙僧来刷碗;
如果掷到 7的倍数就由我来刷碗;
徒弟三人着洗碗的概率分别是多少!
谢 谢
温故知新
必然事件:
在一定条件下必然发生的事件.
不可能事件:
在一定条件下不可能发生的事件.
随机事件:
在一定条件下可能发生也可能不发生的事件.
练 一 练
下面的一些事件是什么事件?
(1)度量三角形的内角和,结果360°
(2)“抛一块石头,下落”;
(3)明天会下雨;
(4)“某人射击一次,中靶”;
(5)“掷一枚硬币,出现正面”。
实验1:掷一枚硬币,落地后:
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
历史上,有些人曾做过成千上万次抛掷硬币的试验,他们的试验结果见表:
试验者
抛掷次数(n)
“正面向上”次数(m)
“正面向上”频率
莫弗
2048
1061
0.518
布丰
4040
2048
0.5069
费勒
10000
4979
0.4979
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
可以发现,在重复抛掷一枚硬币时,“正面向上”的概率在0.5的左右摆动.
随着抛掷次数的增加,“正面向上”的
频率的变化趋势有何规律?
一般地,对于随机事件A,我们把刻画其发生可能性大小的数值,称为事件A的概率。
记为P(A).
概率描述了事件发生可能性的大小
需要注意,概率是针对大量试验而言的,大量试验反映的规律,并非在每次试验中一定存在。
“抛掷一枚硬币50次,则“正面向上”的次数必为25次.”这句话对吗?
概率是针对大量试验而言的,大量试验反映的规律,并非在每次试验中一定存在.
某人连掷硬币50次,结果只有10次正面向上,这种情况完全正常?
这件事并不奇怪,因为预报的降水概率是根据大量统计记录得出的,是符合大多数同等条件协定的实际情况的,某些例外情况是可能发生的.
某气象台报告:今年11月11日有大雨,可这天并没下雨,所以天气预报不可信?
实验2:抛掷一个质地均匀的骰子
(1)它落地时,向上的点数有几种可能的结果?
(2)各点数出现的可能性,会相等吗?
(3)试猜想:你能用一个数值,来说明各点数
出现的可能性大小吗?
正方体有六个面,6种结果。
相等
实验3: 从分别标有1,2,3,4,5的
五根纸签中随机抽取一根
(1)抽取的结果会出现几种可能?
(2)每根纸签抽到的可能性会相等吗?
(3)试猜想:你能用一个数值来说明每根纸签
被抽到的可能性大小吗?
实验3:从分别标有1,2,3,4,5的五根
纸签中随机抽取一根
(4) 你能用一个数值来说明抽到标有1的
可能性大小吗?
(5) 你能用一个数值来说明抽到标有偶数号
的可能性大小吗?
抽出的签上号码有5种可能,即1,2,3,4,5。
标有1的只是其中的一种,所以标有1的概率就为
抽出的签上号码有5种可能,即1,2,3,4,5。标有偶数号的有2,4两种可能,所以标有偶数号的概率就为
摸到红球的概率
学有所用
3
4
摸出一球所有可能出现
的结果数
摸到红球可能出现的结果数
摸到红球的概率
P(摸到红球)=
盒子中装有3个黑棋子和2个白棋子(只有颜色不同,其它均相同),从中摸出一棋子,是黑棋的可能性是多少?
P(摸到黑棋子)=
分析:“从下面的一堆牌中,任意抽一张,抽到红牌”这一事件是什么事件,能不能求出概率?
必然事件
P(抽到红牌)=
分析:“从下面的一堆牌中,任意抽一张,抽到红牌”这一事件是什么事件,能不能求出概率?
不可能事件
P(抽到红牌)=
分析:“从下面的8张牌中,任意抽一张,抽到红牌”这一事件是什么事件,能不能求出概率?
随机事件
P(抽到红牌)=
归纳总结
掷一个骰子,观察向上的一面的 点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5。
试 一试 飞的更高
袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则:
P(摸到红球)= ;
P(摸到白球)= ;
P(摸到黄球)= ;
如图:是一个转盘,转盘分成7个相同的扇形,颜色分为红、黄、绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时,当作指向右边的扇形)求下列事件的概率:
(1)指向红色;
(2)指向红色或黄色;
(3)不指向红色.
解:按颜色共有7种等可能性的结果,分别记
为:红1,红2,红3,绿1,绿2,黄1,黄2.
(1)指针指向红色(记为事件A)的
结果有3个,即红1,红2,红3,则
P(A)=
解:按颜色共有7种等可能性的结果,分别记
为:红1,红2,红3,绿1,绿2,黄1,黄2.
(2)指针指向红色或黄色(记为事件B)
的结果共有5个
即红1,红2,红3 ,黄1,黄2 ,则
P(B)=
解:按颜色共有7种等可能性的结果,分别记
为:红1,红2,红3,绿1,绿2,黄1,黄2.
(3)指针不指向红色(记为事件C)的
结果共有4个
即绿1,绿2,黄1,黄2 ,则
P(C)=
计算机扫雷游戏,在9×9个小方格中,随机埋藏着10个地雷,每个小方格只有1个地雷,,小王开始随机踩一个小方格,标号为3,在3的周围的正方形中有3个地雷,我们把他的区域记为A区,A区外记为B区,下一步小王应该踩在A区还是B区?
如图:计算机扫雷游戏,在9×9个小方格中,随机埋藏着10个地雷,每个小方格只有1个地雷,,小王开始随机踩一个小方格,标号为3,在3的周围的正方形中有3个地雷,我们把他的去域记为A区,A区外记为B区,,下一步小王应该踩在A区还是B区?
由于3/8大于7/72,
所以第二步应踩B区
解:A区有8格3个雷,遇到地雷的概率为3/8,
B区有9×9-9=72个小方格,
还有10-3=7个地雷,
遇到地雷的概率为7/72,
甲、乙 两人做如下的游戏:
你认为这个游戏对甲、乙双方公平吗?
任意掷出骰子后,若朝上的数字是6,则甲获胜;
若朝上的数字不是6,则乙获胜。
解:∵P(甲获胜) = P(乙获胜) =
∴P(乙获胜) > P(甲获胜)
∴ 游戏对甲、乙双方不公平
话说唐僧师徒越过狮驼岭,吃完午饭后,三徒弟商量着今天由谁来刷碗,可半天也没个好主意。还是悟空聪明,他灵机一动,扒根猴毛一吹,变成一粒骰子,对八戒说道:我们三人来掷骰子:
如果掷到 2的倍数就由八戒来刷碗;
如果掷到 3的倍数就由沙僧来刷碗;
如果掷到 7的倍数就由我来刷碗;
徒弟三人着洗碗的概率分别是多少!
谢 谢
同课章节目录
