人教八上数学第十二章全等三角形证明判定方法分类总结(无答案)
文档属性
| 名称 | 人教八上数学第十二章全等三角形证明判定方法分类总结(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 23:26:37 | ||
图片预览




文档简介
全等三角形(一)SSS
【知识要点】
1.全等图形定义:两个能够重合的图形称为全等图形.
2.全等图形的性质:
(1)全等图形的形状和大小都相同,对应边相等,对应角相等
(2)全等图形的面积相等
3.全等三角形:两个能够完全重合的三角形称为全等三角形
(1)表示方法:两个三角形全等用符号“≌”来表示,读作“全等于”
如全等,记作≌
(2)符号“≌”的含义:“∽”表示形状相同,“=”表示大小相等,合起来就是形状相同,大小也相等,这就是全等.
(3)两个全等三角形重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角.
(4)证两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
4.全等三角形的判定(一):三边对应相等的两个三角形全等,简与成“边边边”或“SSS”.
【典型例题】
例1.如图,≌,点B与点D是对应点,,且,,求的度数及的面积.
例2.如图,≌,,求的度数及CF的长.
例3.如图,已知:AB=AD,AC=AE,BC=DE,求证:
例4.如图AB=DE,BC=EF,AD=CF,求证:
(1)≌
(2)AB//DE,BC//EF
例5.如图,在D、E分别为AC、AB上的点,且BE=BC,DE=DC,求证:(1);
(2)BD平分
【巩固练习】
1.下面给出四个结论:①若两个图形是全等图形,则它们形状一定相同;②若两个图形的形状相同,则它们一定是全等图形;③若两个图形的面积相等,则它们一定是全等图形;④若两个图形是全等图形,则它们的大小一定相同,其中正确的是(
)
A、①④
B、①②
C、②③
D、③④
2.如图,≌,且AB和CD是对应边,下面四个结论中
不正确的是(
)
A、的面积相等
B、的周长相等
C、
D、AD//BC且AD=BC
3.如图,≌,A和B
以及C和D分别是对应点,如果,则的度数为(
)
A、
B、
C、
D、
4.如图,≌,AD=8,BE=2,则AE等于(
)
A、6
B、5
C、4
D、3
5.如图,要使≌,则下列条件能满足的是(
)
A、AC=BC,AD=CE,BD=BE
B、AD=BD,AC=CE,BE=BD
C、DC=EC,AC=BC,BE=AD
D、AD=BE,AC=DC,BC=EC
6.如图,≌,点A和点D、点E和点F分别是对应点,则AB=
,
,AE=
,CE=
,AB//
,若,则DF与BC的关系是
.
7.如图,≌,若
,
,
.
8.如图,若AB=AC,BE=CD,AE=AD,则
,所以
,
,
.
9.如图,≌,,则下列说法错误的是(
)
A、
B、C、D
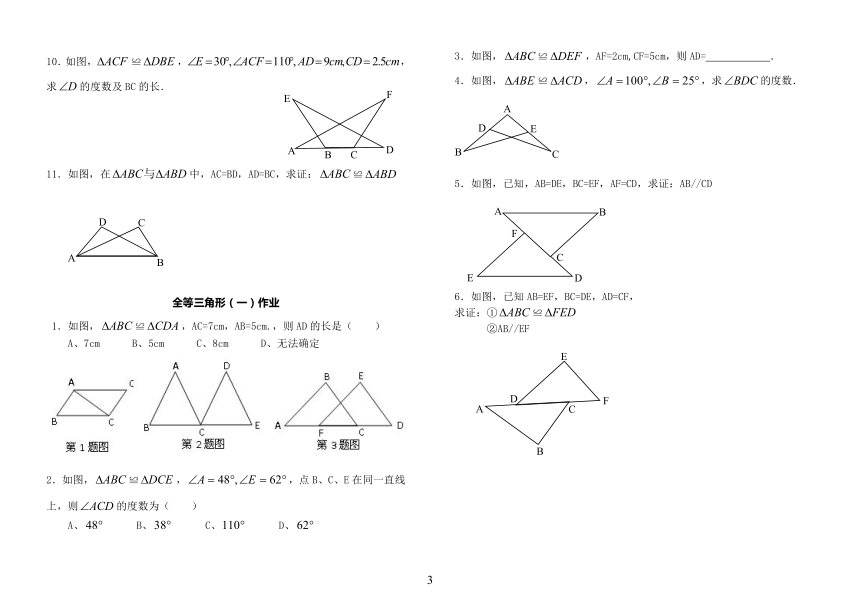
10.如图,≌,,求的度数及BC的长.
11.如图,在中,AC=BD,AD=BC,求证:≌
全等三角形(一)作业
1.如图,≌,AC=7cm,AB=5cm.,则AD的长是(
)
A、7cm
B、5cm
C、8cm
D、无法确定
2.如图,≌,,点B、C、E在同一直线上,则的度数为(
)
A、
B、
C、
D、
3.如图,≌,AF=2cm,CF=5cm,则AD=
.
4.如图,≌,,求的度数.
5.如图,已知,AB=DE,BC=EF,AF=CD,求证:AB//CD
6.如图,已知AB=EF,BC=DE,AD=CF,
求证:①≌
②AB//EF
7.如图,已知AB=AD,AC=AE,BC=DE,求证:
全等三角形(二)
【知识要点】
定义:SAS
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”,几何表示
如图,在和中,
≌
【典型例题】
【例1】
已知:如图,AB=AC,AD=AE,求证:BE=CD.
【例2】
如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,由此你能得出哪些结论?给出证明.
【例3】
如图已知:AE=AF,AB=AC,∠A=60°,∠B=24°,求∠BOE的度数.
【例4】
如图,B,C,D在同一条直线上,△ABC,△ADE是等边三角形,
求证:①CE=AC+DC;
②∠ECD=60°.
【例5】如图,已知△ABC、△BDE均为等边三角形。求证:BD+CD=AD。
【巩固练习】
1.在△ABC和△中,若AB=,AC=,还要加一个角的条件,使△ABC≌△,那么你加的条件是(
)
A.∠A=∠
B.∠B=∠
C.∠C=∠
D.∠A=∠
2.下列各组条件中,能判断△ABC≌△DEF的是(
)
A.AB=DE,BC=EF;CA=CD
B.CA=CD;∠C=∠F;AC=EF
C.CA=CD;∠B=∠E
D.AB=DE;BC=EF,两个三角形周长相等
3.阅读理解题:
如图:已知AC,BD相交于O,OA=OB,OC=OD.
那么△AOD与△BOC全等吗?请说明理由.△ABC与△BAD全等吗?请说明理由.
小明的解答:
△AOD≌△BOC
而△BAD=△AOD+△ADB
△ABC=△BOC+△AOB
所以△ABC≌△BAD
(1)你认为小明的解答有无错误;
(2)如有错误给出正确解答;
4.如图,点C是AB中点,CD∥BE,且CD=BE,试探究AD与CE的关系。
5.如图,AE是AB=AC
(1)若D是AE上任意一点,则△ABD≌△ACD,说明理由.
(2)若D是AE反向延长线上一点,结论还成立吗?请说明理由.
6.如图,已知AB=AC,EB=EC,请说明BD=CD的理由
全等三角形(二)作业
1.如图,已知AB=AC,AD=AE,BF=CF,求证:≌。
2.如图,△ABC,△BDF为等腰直角三角形。求证:(1)CF=AD;(2)CE⊥AD。
3.如图,AB=AC,AD=AE,BE和CD相交于点O,AO的延长线交BC于点F。
求证:BF=FC。
4.已知:如图1,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,求证:DE∥BF。
5.
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,
求证:(1)BE=DC,(2)BE⊥DC.
6、已知,如图A、F、C、D四点在一直线上,AF=CD,AB//DE,且AB=DE,求证:(1)△ABC≌△DEF
(2)∠CBF=∠FEC
7、
已知:如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:BD=CE
8、如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG,
(1)观察猜想BE与DG之间的大小关系,并证明你的结论。
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程,若不存在,说明理由。
9、已知:如图,AD是BC上的中线
,且DF=DE.求证:BE∥CF.
10、已知C为AB上一点,△ACN和
△BCM是正三角形.求证:(1)AM=BN
(2)求∠AFN大小。
11、已知如图,F在正方形ABCD的边BC边上,E在AB的延长线上,FB=EB,AF交CE于G,求∠AGC的度数.
12、
如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.
全等三角形(三)ASA
【知识要点】
ASA公理:有两角和它们的夹边对应相等的两个三角形全等.
如图,在与中
ASA公理推论(AAS公理):有两角和其中一角的对边对应相等的两个三角形全等.
【典型例题】
【例1】下列条件不可推得和全等的条件是(
)
AB=AB,,
AB=
AB,AC=AC,BC=C
AB=
AB,AC=AC,
AB=
AB,,
【例2】已知如图,,求证:BC=EF
【例3】如图,AB=AC,,求证:AD=AE
【例4】已知如图,,点P在AB上,可以得出PC=PD吗?试证明之.
【例5】如图,,AC=AE,求证:DE=BC
【例6】如图,,AC,BD相交于O,
求证:①AB=CD
②OA=OD
【巩固练习】
1.如图,AB//CD,AF//DE,BE=CF,求证:AB=CD
2.如图,AD//BC,O为AC中点,过点O的直线分别交AD,BC于点M,N,求证:AM=CN
3.求证:两个全等三角形ABC与ABC的角平分线AD、AD相等
4.如图,AB,CD相交于O,E,F分别在AD,BC上,若,求证:
5.如图,AB//CD,AD//BC,求证:AB=CD
6.已知,如图AB=DB,,求证:AC=DE
全等三角形(三)作业
1.已知,如图,,求证:AB=DE
2.如图,已知,求证:BE=CD
3.已知如图,AB=AD,,求证:AC=AE
4.已知如图,在中,AD平分,求证:
5.已知如图,,求BD的长(要求写出完整的过程)
6、如图中,∠B=∠C,D,E,F分别在AB,BC,AC上,且BD=CE,∠DEF=∠B
求证:ED=EF
7、
(1)如图1,以的边、为边分别向外作正方形和正方形,连结,试判断△ABC与△AEG面积之间的关系,并说明理由.
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
8、已知:如图
,
AD为CE的垂直平分线
,
EF∥BC.求证:△EDN≌△CDN≌△EMN.
9、
已知:如图
,
AB=AC
,
AD=AE
,
求证:△OBD≌△OCE
10、已知:如图
,
AB=CD
,
AD=BC
,O为BD中点
,
过O作直线分别与DA、BC的延长线交于E、F.求证:OE=OF
11、如图在△ABC和△DBC中
,
∠1=∠2
,
∠3=∠4
,
P是BC上任意一点.求证:PA=PD.
12、已知
:如图
,
四边形
ABCD中
,
AD∥BC
,
F是AB的中点
,
DF交CB延长线
于E
,
CE=CD.
求证:∠ADE=∠EDC.
13、已知:如图
,
OA=OE
,
OB=OF
,
直线FA与BE交于C
,
AB和EF交于O
,求证:∠1=∠2.
全等三角形(四)
强化训练
1、如图,△是等边三角形,点、、分别是线段、、上的点,
(1)若,问△是等边三角形吗?试证明你的结论;
(2)若△是等边三角形,问成立吗?试证明你的结论.
2、如图所示,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:2∠M=(∠ACB-∠B)
3、△ABC中,∠A=90°,AB=AC,D为BC中点,E、F分别在AC、AB上,且DE⊥DF,试判断DE、DF的数量关系,并说明理由.
4、已知:如图,中,,于,平分,且于,与相交于点是边的中点,连结与相交于点.
(1)求证:;(2)求证:;
5、
如图,点是等边内一点,.将绕点按顺时针方向旋转得,连接.
(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)探究:当为多少度时,是等腰三角形?
7、过等腰直角三角形直角顶点A作直线AM平行于斜边BC,在AM上取点D,使BD=BC,且DB与AC所在直线交于E,求证:CD=CE。
过A作AF⊥BC于F,过D作DG⊥BC于G,则DG=AF=1/2BC=1/2BD,
在Rt△BDG中,DG=1/2BD
=>
∠DBC=30°
=>∠BDC=∠BCD=1/2(180°-30°)=75°,即∠EDC=75°
∠DEC=∠DBC+∠BCA=30°+45°=75°
∴∠EDC=∠DEC
=>CD=CE
8、Rt△ABC,AB=AC,BM是中线,AD⊥BM交BC于D,求证:∠AMB=∠CMD。
9、如图,已知△ABC是等边三角形,∠BDC=120?,说明AD=BD+CD的理由。
10、已知:如图,点D在△ABC的边CA的延长线上,点E在BA的延长线上,CF、EF分别是∠ACB、∠AED的平分线,且∠B=30°,∠D=40°,求∠F的度数。
11、等边三角形ABC和等边三角形DEC,D在AC边上。延长BD交CE延长线于N,延长AE交BC延长线于M。求证:CM=CN
易证△BCD≌△ACE
所以∠DBC=∠EAC
再证△BCN≌△ACM
(ASA)
∴
CM=CN
12、操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
13、如图等边△ABC和等边△CDE,点P为射线BC一动点,角APK=60°,PK交直线CD于K。
试探索AP、PK之间的数量关系;
当点P运动到BC延长线上时,上题结论是否依然成立?为什么。
14、(涉及相似三角形)若P为所在平面上一点,且,则点叫做的费马点.
如图,在锐角外侧作等边′连结′。
求证:′过的费马点,且′=.
15、如图,是等腰直角三角形,∠C=900,点M,N分别是边AC和BC的中点,点D在射线BM上,且BD=2BM,
点E在射线NA上,且NE=2NA.求证:BD⊥DE.
第五章
全等三角形
拓展延伸
分析:三角形全等的证明及其运用关键点在于“把相等的边(角)放入正确的三角形中”,去说明“相等的边(角)所在的三角形全等”,利用三角形全等来说明两个角相等(两条边相等)是初中里面一个非常常见而又重要的方法。
例1:已知AE既是∠BAC的平分线,也是∠BDC的平分线,试说明AB=AC
思路:AB在△ABD中,AC在△ACD中,要说明AB=AC,尝试说明△ABD与△ACD全等。
观察图形发现两个三角形存在公共边AD
题目所给条件可以得到两组角相等,
再根据三个条件的位置,利用ASA,可得三角形全等
再利用全等三角形的对应边相等,得到AB=AC
例2:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,如果CE=5,BD=11,请你求出DE的长度。
思路:抓住题目中所给的一组相等线段AB=AC进行分析,对它们的位置进行分析,发现AB、AC分别位于一个Rt△中,所以尝试着去找条件,去说明它们所在的两个Rt△全等。
那么:已经存在了两组等量关系:AB=AC,直角=直角.可以求证△ABD≌△ACE。
练习1.
小明说:“三角形一边的两个端点到这边上的中线所在直线的距离相等。”你认为小明的话有道理吗?为什么?
分析:如图,题目的意思是要你说明哪两条线段相等呢?
_______=_______
∴我们只需要说明
________≌________
解:
练习2.
在△ABC中,∠ACB=
900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图1的位置时,△ADC≌△CEB,且
DE=AD+BE。你能说出其中的道理吗?
(2)当直线MN绕点C旋转到图2的位置时,
DE
=AD-BE。说说你的理由。
(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE
具有怎样的等量关系?请写出这个等量关系。
A
B
D
C
A
B
E
C
F
D
A
B
E
C
D
A
B
C
D
F
E
A
E
B
C
D
A
B
D
C
A
B
C
D
第3题图
A
C
E
B
F
D
第6题图
第5题图
A
B
C
D
E
B
A
C
E
F
D
第4题图
B
A
C
D
E
第7题图
E
F
D
B
C
A
第9题题图
第8题图
A
B
D
E
C
A
B
C
D
F
E
A
D
C
B
A
B
C
D
E
A
B
C
D
E
F
B
A
C
E
F
D
A
B
E
C
D
A
B
C
E
D
F
A
D
B
E
C
A
B
D
E
C
1
2
B
E
A
F
C
O
E
A
B
C
D
D
A
B
C
E
SAS
OA=OB
OD=OC
D
C
1
2
O
A
B—
A
C
B
E
D
B
C
D
E
A
1
2
A
B
E
D
C
A
B
C
E
D
F
A
C
B
D
E
F
A
D
E
C
B
F
O
1
2
D
C
A
B
E
F
D
A
B
Q
C
P
E
C
N
M
B
A
E
D
F
A
B
C
D
E
F
A
D
B
E
C
F
A
B
D
E
C
A
B
C
D
P
1
2
3
4
1
2
A
4
3
B
C
D
E
O
A
B
C
D
O
1
2
A
B
D
C
F
E
A
B
C
N
M
D
O
A
B
C
D
A
B
D
EMBED
Equation.3
EMBED
Equation.3
C
A
E
D
O
C
F
B
A
B
D
C
1
3
2
4
C
A
D
E
B
1
2
A
E
F
D
C
B
1
2
A
B
E
D
C
A
B
D
C
E
A
B
D
C
A
C
B
D
A
D
E
C
B
F
A
G
F
C
B
D
E
(图1)
A
C
B
图3
图2
图1
PAGE
2
【知识要点】
1.全等图形定义:两个能够重合的图形称为全等图形.
2.全等图形的性质:
(1)全等图形的形状和大小都相同,对应边相等,对应角相等
(2)全等图形的面积相等
3.全等三角形:两个能够完全重合的三角形称为全等三角形
(1)表示方法:两个三角形全等用符号“≌”来表示,读作“全等于”
如全等,记作≌
(2)符号“≌”的含义:“∽”表示形状相同,“=”表示大小相等,合起来就是形状相同,大小也相等,这就是全等.
(3)两个全等三角形重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角.
(4)证两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
4.全等三角形的判定(一):三边对应相等的两个三角形全等,简与成“边边边”或“SSS”.
【典型例题】
例1.如图,≌,点B与点D是对应点,,且,,求的度数及的面积.
例2.如图,≌,,求的度数及CF的长.
例3.如图,已知:AB=AD,AC=AE,BC=DE,求证:
例4.如图AB=DE,BC=EF,AD=CF,求证:
(1)≌
(2)AB//DE,BC//EF
例5.如图,在D、E分别为AC、AB上的点,且BE=BC,DE=DC,求证:(1);
(2)BD平分
【巩固练习】
1.下面给出四个结论:①若两个图形是全等图形,则它们形状一定相同;②若两个图形的形状相同,则它们一定是全等图形;③若两个图形的面积相等,则它们一定是全等图形;④若两个图形是全等图形,则它们的大小一定相同,其中正确的是(
)
A、①④
B、①②
C、②③
D、③④
2.如图,≌,且AB和CD是对应边,下面四个结论中
不正确的是(
)
A、的面积相等
B、的周长相等
C、
D、AD//BC且AD=BC
3.如图,≌,A和B
以及C和D分别是对应点,如果,则的度数为(
)
A、
B、
C、
D、
4.如图,≌,AD=8,BE=2,则AE等于(
)
A、6
B、5
C、4
D、3
5.如图,要使≌,则下列条件能满足的是(
)
A、AC=BC,AD=CE,BD=BE
B、AD=BD,AC=CE,BE=BD
C、DC=EC,AC=BC,BE=AD
D、AD=BE,AC=DC,BC=EC
6.如图,≌,点A和点D、点E和点F分别是对应点,则AB=
,
,AE=
,CE=
,AB//
,若,则DF与BC的关系是
.
7.如图,≌,若
,
,
.
8.如图,若AB=AC,BE=CD,AE=AD,则
,所以
,
,
.
9.如图,≌,,则下列说法错误的是(
)
A、
B、C、D
10.如图,≌,,求的度数及BC的长.
11.如图,在中,AC=BD,AD=BC,求证:≌
全等三角形(一)作业
1.如图,≌,AC=7cm,AB=5cm.,则AD的长是(
)
A、7cm
B、5cm
C、8cm
D、无法确定
2.如图,≌,,点B、C、E在同一直线上,则的度数为(
)
A、
B、
C、
D、
3.如图,≌,AF=2cm,CF=5cm,则AD=
.
4.如图,≌,,求的度数.
5.如图,已知,AB=DE,BC=EF,AF=CD,求证:AB//CD
6.如图,已知AB=EF,BC=DE,AD=CF,
求证:①≌
②AB//EF
7.如图,已知AB=AD,AC=AE,BC=DE,求证:
全等三角形(二)
【知识要点】
定义:SAS
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”,几何表示
如图,在和中,
≌
【典型例题】
【例1】
已知:如图,AB=AC,AD=AE,求证:BE=CD.
【例2】
如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,由此你能得出哪些结论?给出证明.
【例3】
如图已知:AE=AF,AB=AC,∠A=60°,∠B=24°,求∠BOE的度数.
【例4】
如图,B,C,D在同一条直线上,△ABC,△ADE是等边三角形,
求证:①CE=AC+DC;
②∠ECD=60°.
【例5】如图,已知△ABC、△BDE均为等边三角形。求证:BD+CD=AD。
【巩固练习】
1.在△ABC和△中,若AB=,AC=,还要加一个角的条件,使△ABC≌△,那么你加的条件是(
)
A.∠A=∠
B.∠B=∠
C.∠C=∠
D.∠A=∠
2.下列各组条件中,能判断△ABC≌△DEF的是(
)
A.AB=DE,BC=EF;CA=CD
B.CA=CD;∠C=∠F;AC=EF
C.CA=CD;∠B=∠E
D.AB=DE;BC=EF,两个三角形周长相等
3.阅读理解题:
如图:已知AC,BD相交于O,OA=OB,OC=OD.
那么△AOD与△BOC全等吗?请说明理由.△ABC与△BAD全等吗?请说明理由.
小明的解答:
△AOD≌△BOC
而△BAD=△AOD+△ADB
△ABC=△BOC+△AOB
所以△ABC≌△BAD
(1)你认为小明的解答有无错误;
(2)如有错误给出正确解答;
4.如图,点C是AB中点,CD∥BE,且CD=BE,试探究AD与CE的关系。
5.如图,AE是AB=AC
(1)若D是AE上任意一点,则△ABD≌△ACD,说明理由.
(2)若D是AE反向延长线上一点,结论还成立吗?请说明理由.
6.如图,已知AB=AC,EB=EC,请说明BD=CD的理由
全等三角形(二)作业
1.如图,已知AB=AC,AD=AE,BF=CF,求证:≌。
2.如图,△ABC,△BDF为等腰直角三角形。求证:(1)CF=AD;(2)CE⊥AD。
3.如图,AB=AC,AD=AE,BE和CD相交于点O,AO的延长线交BC于点F。
求证:BF=FC。
4.已知:如图1,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,求证:DE∥BF。
5.
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,
求证:(1)BE=DC,(2)BE⊥DC.
6、已知,如图A、F、C、D四点在一直线上,AF=CD,AB//DE,且AB=DE,求证:(1)△ABC≌△DEF
(2)∠CBF=∠FEC
7、
已知:如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:BD=CE
8、如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG,
(1)观察猜想BE与DG之间的大小关系,并证明你的结论。
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程,若不存在,说明理由。
9、已知:如图,AD是BC上的中线
,且DF=DE.求证:BE∥CF.
10、已知C为AB上一点,△ACN和
△BCM是正三角形.求证:(1)AM=BN
(2)求∠AFN大小。
11、已知如图,F在正方形ABCD的边BC边上,E在AB的延长线上,FB=EB,AF交CE于G,求∠AGC的度数.
12、
如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.
全等三角形(三)ASA
【知识要点】
ASA公理:有两角和它们的夹边对应相等的两个三角形全等.
如图,在与中
ASA公理推论(AAS公理):有两角和其中一角的对边对应相等的两个三角形全等.
【典型例题】
【例1】下列条件不可推得和全等的条件是(
)
AB=AB,,
AB=
AB,AC=AC,BC=C
AB=
AB,AC=AC,
AB=
AB,,
【例2】已知如图,,求证:BC=EF
【例3】如图,AB=AC,,求证:AD=AE
【例4】已知如图,,点P在AB上,可以得出PC=PD吗?试证明之.
【例5】如图,,AC=AE,求证:DE=BC
【例6】如图,,AC,BD相交于O,
求证:①AB=CD
②OA=OD
【巩固练习】
1.如图,AB//CD,AF//DE,BE=CF,求证:AB=CD
2.如图,AD//BC,O为AC中点,过点O的直线分别交AD,BC于点M,N,求证:AM=CN
3.求证:两个全等三角形ABC与ABC的角平分线AD、AD相等
4.如图,AB,CD相交于O,E,F分别在AD,BC上,若,求证:
5.如图,AB//CD,AD//BC,求证:AB=CD
6.已知,如图AB=DB,,求证:AC=DE
全等三角形(三)作业
1.已知,如图,,求证:AB=DE
2.如图,已知,求证:BE=CD
3.已知如图,AB=AD,,求证:AC=AE
4.已知如图,在中,AD平分,求证:
5.已知如图,,求BD的长(要求写出完整的过程)
6、如图中,∠B=∠C,D,E,F分别在AB,BC,AC上,且BD=CE,∠DEF=∠B
求证:ED=EF
7、
(1)如图1,以的边、为边分别向外作正方形和正方形,连结,试判断△ABC与△AEG面积之间的关系,并说明理由.
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
8、已知:如图
,
AD为CE的垂直平分线
,
EF∥BC.求证:△EDN≌△CDN≌△EMN.
9、
已知:如图
,
AB=AC
,
AD=AE
,
求证:△OBD≌△OCE
10、已知:如图
,
AB=CD
,
AD=BC
,O为BD中点
,
过O作直线分别与DA、BC的延长线交于E、F.求证:OE=OF
11、如图在△ABC和△DBC中
,
∠1=∠2
,
∠3=∠4
,
P是BC上任意一点.求证:PA=PD.
12、已知
:如图
,
四边形
ABCD中
,
AD∥BC
,
F是AB的中点
,
DF交CB延长线
于E
,
CE=CD.
求证:∠ADE=∠EDC.
13、已知:如图
,
OA=OE
,
OB=OF
,
直线FA与BE交于C
,
AB和EF交于O
,求证:∠1=∠2.
全等三角形(四)
强化训练
1、如图,△是等边三角形,点、、分别是线段、、上的点,
(1)若,问△是等边三角形吗?试证明你的结论;
(2)若△是等边三角形,问成立吗?试证明你的结论.
2、如图所示,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:2∠M=(∠ACB-∠B)
3、△ABC中,∠A=90°,AB=AC,D为BC中点,E、F分别在AC、AB上,且DE⊥DF,试判断DE、DF的数量关系,并说明理由.
4、已知:如图,中,,于,平分,且于,与相交于点是边的中点,连结与相交于点.
(1)求证:;(2)求证:;
5、
如图,点是等边内一点,.将绕点按顺时针方向旋转得,连接.
(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)探究:当为多少度时,是等腰三角形?
7、过等腰直角三角形直角顶点A作直线AM平行于斜边BC,在AM上取点D,使BD=BC,且DB与AC所在直线交于E,求证:CD=CE。
过A作AF⊥BC于F,过D作DG⊥BC于G,则DG=AF=1/2BC=1/2BD,
在Rt△BDG中,DG=1/2BD
=>
∠DBC=30°
=>∠BDC=∠BCD=1/2(180°-30°)=75°,即∠EDC=75°
∠DEC=∠DBC+∠BCA=30°+45°=75°
∴∠EDC=∠DEC
=>CD=CE
8、Rt△ABC,AB=AC,BM是中线,AD⊥BM交BC于D,求证:∠AMB=∠CMD。
9、如图,已知△ABC是等边三角形,∠BDC=120?,说明AD=BD+CD的理由。
10、已知:如图,点D在△ABC的边CA的延长线上,点E在BA的延长线上,CF、EF分别是∠ACB、∠AED的平分线,且∠B=30°,∠D=40°,求∠F的度数。
11、等边三角形ABC和等边三角形DEC,D在AC边上。延长BD交CE延长线于N,延长AE交BC延长线于M。求证:CM=CN
易证△BCD≌△ACE
所以∠DBC=∠EAC
再证△BCN≌△ACM
(ASA)
∴
CM=CN
12、操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
13、如图等边△ABC和等边△CDE,点P为射线BC一动点,角APK=60°,PK交直线CD于K。
试探索AP、PK之间的数量关系;
当点P运动到BC延长线上时,上题结论是否依然成立?为什么。
14、(涉及相似三角形)若P为所在平面上一点,且,则点叫做的费马点.
如图,在锐角外侧作等边′连结′。
求证:′过的费马点,且′=.
15、如图,是等腰直角三角形,∠C=900,点M,N分别是边AC和BC的中点,点D在射线BM上,且BD=2BM,
点E在射线NA上,且NE=2NA.求证:BD⊥DE.
第五章
全等三角形
拓展延伸
分析:三角形全等的证明及其运用关键点在于“把相等的边(角)放入正确的三角形中”,去说明“相等的边(角)所在的三角形全等”,利用三角形全等来说明两个角相等(两条边相等)是初中里面一个非常常见而又重要的方法。
例1:已知AE既是∠BAC的平分线,也是∠BDC的平分线,试说明AB=AC
思路:AB在△ABD中,AC在△ACD中,要说明AB=AC,尝试说明△ABD与△ACD全等。
观察图形发现两个三角形存在公共边AD
题目所给条件可以得到两组角相等,
再根据三个条件的位置,利用ASA,可得三角形全等
再利用全等三角形的对应边相等,得到AB=AC
例2:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,如果CE=5,BD=11,请你求出DE的长度。
思路:抓住题目中所给的一组相等线段AB=AC进行分析,对它们的位置进行分析,发现AB、AC分别位于一个Rt△中,所以尝试着去找条件,去说明它们所在的两个Rt△全等。
那么:已经存在了两组等量关系:AB=AC,直角=直角.可以求证△ABD≌△ACE。
练习1.
小明说:“三角形一边的两个端点到这边上的中线所在直线的距离相等。”你认为小明的话有道理吗?为什么?
分析:如图,题目的意思是要你说明哪两条线段相等呢?
_______=_______
∴我们只需要说明
________≌________
解:
练习2.
在△ABC中,∠ACB=
900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图1的位置时,△ADC≌△CEB,且
DE=AD+BE。你能说出其中的道理吗?
(2)当直线MN绕点C旋转到图2的位置时,
DE
=AD-BE。说说你的理由。
(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE
具有怎样的等量关系?请写出这个等量关系。
A
B
D
C
A
B
E
C
F
D
A
B
E
C
D
A
B
C
D
F
E
A
E
B
C
D
A
B
D
C
A
B
C
D
第3题图
A
C
E
B
F
D
第6题图
第5题图
A
B
C
D
E
B
A
C
E
F
D
第4题图
B
A
C
D
E
第7题图
E
F
D
B
C
A
第9题题图
第8题图
A
B
D
E
C
A
B
C
D
F
E
A
D
C
B
A
B
C
D
E
A
B
C
D
E
F
B
A
C
E
F
D
A
B
E
C
D
A
B
C
E
D
F
A
D
B
E
C
A
B
D
E
C
1
2
B
E
A
F
C
O
E
A
B
C
D
D
A
B
C
E
SAS
OA=OB
OD=OC
D
C
1
2
O
A
B—
A
C
B
E
D
B
C
D
E
A
1
2
A
B
E
D
C
A
B
C
E
D
F
A
C
B
D
E
F
A
D
E
C
B
F
O
1
2
D
C
A
B
E
F
D
A
B
Q
C
P
E
C
N
M
B
A
E
D
F
A
B
C
D
E
F
A
D
B
E
C
F
A
B
D
E
C
A
B
C
D
P
1
2
3
4
1
2
A
4
3
B
C
D
E
O
A
B
C
D
O
1
2
A
B
D
C
F
E
A
B
C
N
M
D
O
A
B
C
D
A
B
D
EMBED
Equation.3
EMBED
Equation.3
C
A
E
D
O
C
F
B
A
B
D
C
1
3
2
4
C
A
D
E
B
1
2
A
E
F
D
C
B
1
2
A
B
E
D
C
A
B
D
C
E
A
B
D
C
A
C
B
D
A
D
E
C
B
F
A
G
F
C
B
D
E
(图1)
A
C
B
图3
图2
图1
PAGE
2
