3.3　两点间的距离

(共12张PPT)
两点间的距离
资兴一中：段飞鸿
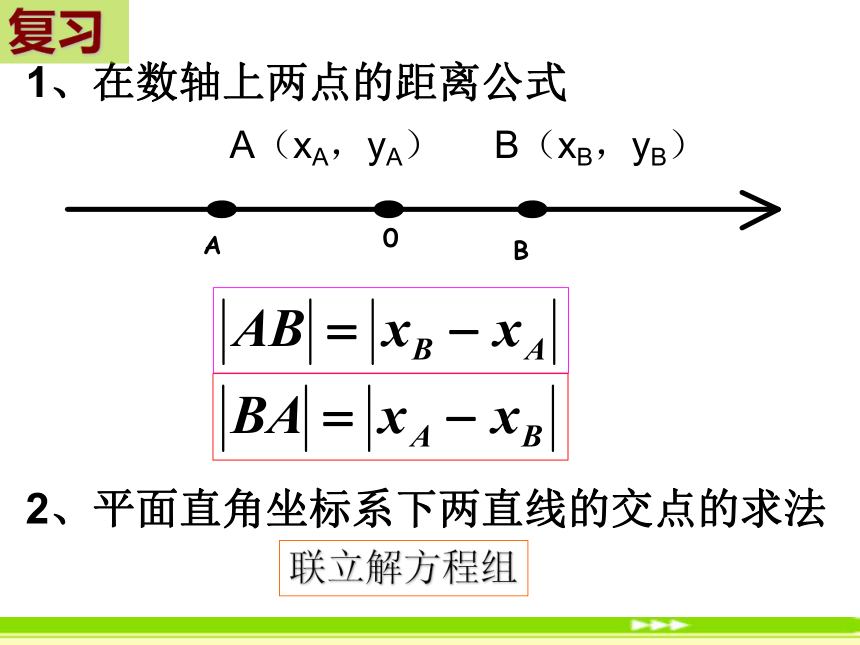
1、在数轴上两点的距离公式
A（xA，yA） B（xB，yB）
2、平面直角坐标系下两直线的交点的求法
联立解方程组
复习
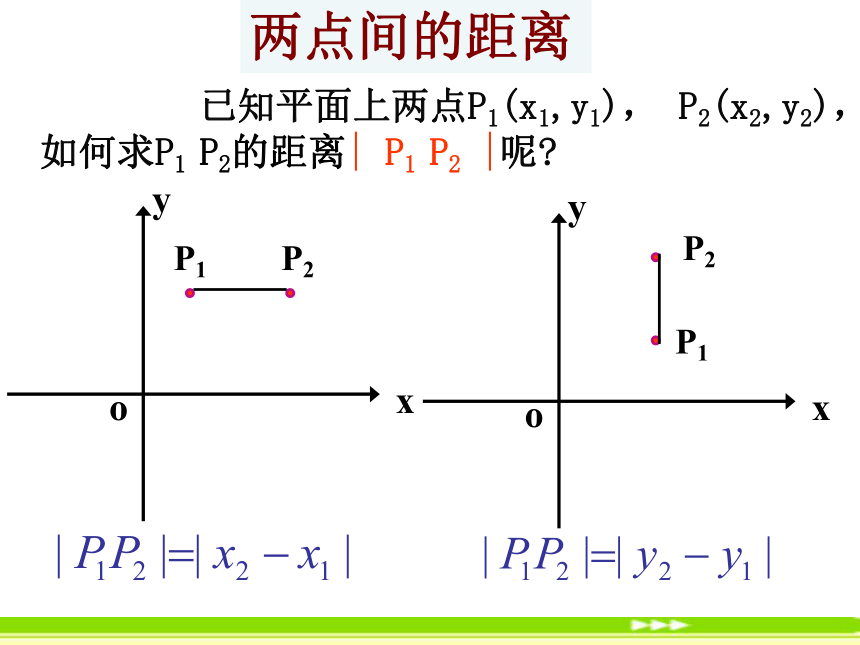
已知平面上两点P1(x1,y1)， P2(x2,y2)，如何求P1 P2的距离| P1 P2 |呢
两点间的距离
y
x
o
P1
P2
y
x
o
P2
P1
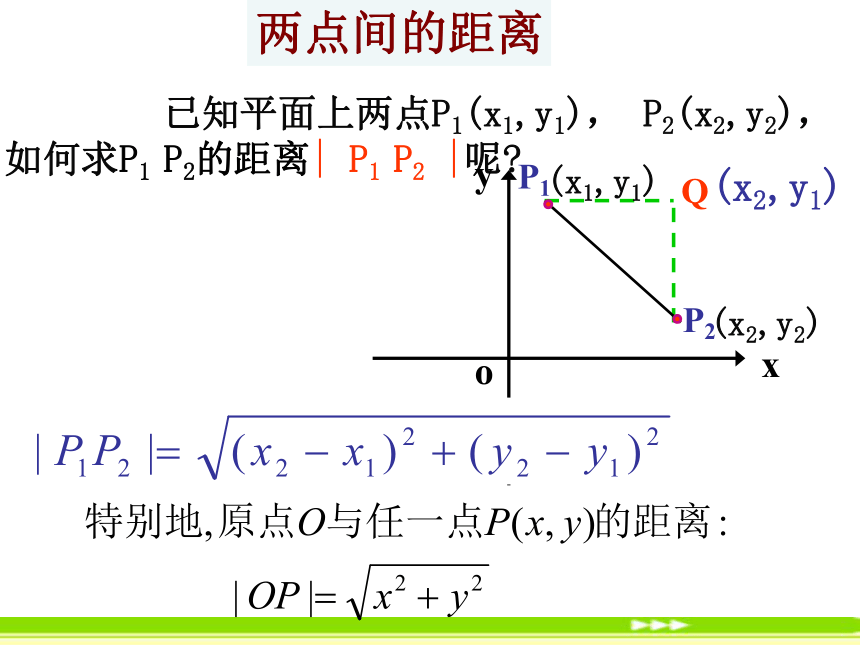
已知平面上两点P1(x1,y1)， P2(x2,y2)，如何求P1 P2的距离| P1 P2 |呢
两点间的距离
Q
(x2,y1)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
练习
1、求下列两点间的距离：
(1)、A(6，0),B(-2，0) (2)、C(0，-4),D(0，-1)
(3)、P(6，0),Q(0，-2) (4)、M(2，1),N(5，-1)
解：
（1）
（2）
（3）
（4）
例题分析
解：设所求点为P(x,0)，于是有
解得x=1，所以所求点P(1,0)
练习
已知点P的横坐标是7，点P与点N(-1,5)间的距离等于10，求点P的纵坐标。
例题分析
例：证明平行四边形四条边的平方和
等于两条对角线的平方和.
A
B
C
D
分析：首先要建立适当
的平面直角坐标系，用
坐标表示有关量，然后
进行代数运算.
第一步：建立坐标系，用坐标表示有关的量；
第二步：进行有关的代数运算；
第三步：把代数运算结果“翻译”成几何关系.
平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是
收获
　　　1、牢记两点间的距离公式；
　　　2、解析法证题的建系方法；
小结
　　已知△ABC的三个顶点A(-1,0),B(1,0),
C( 　)
试判断△ABC的形状.
分析：计算三边的长，比较后可得结论.
思考