七上 第一章丰富的图形世界 学案(全)
文档属性
| 名称 | 七上 第一章丰富的图形世界 学案(全) |  | |
| 格式 | zip | ||
| 文件大小 | 324.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-05 20:41:21 | ||
图片预览




文档简介
第一章第1个学案
课题: 1-1生活中的立体图形(一)
主备: 审核: 检查:
学习目标:在具体的情境中,认识并能够辨别出基本的几何体。
通过比较,学会观察物体间的特征,体会几何体间的联系和区别,并能根据几何体的特征,对其进行简单分类。
学习重点:认识一些基本的几何体,并能描述这些几何体的特征。
学习难点:描述几何体的特征,对几何体进行分类。
[课前导学]
一、课前预习:阅读课本P1~4页:完成练习:
课本第1页的彩图中,我们在欣赏这个城市的美景时,不妨用数学的眼光观察一下,这个美丽的城市也是我们数学世界——丰富的图形世界,你能从中发现哪些熟悉的图形?
(1)广场中心的喷泉池是________形,大楼是_________体。
(2)从不同的方向观察同一建筑物,看到的图形是______(A、一样的 B、不一样的.)
课本第2页的彩图中,映人我们眼帘的便是各式各样的立体图形,请看图识几何体:
(3)发现了亭子的顶端是__________体,下面的支柱是_________体.
(4)人民大会堂中间的建筑是________体.
(5)从太空看地球是________体。举例说明与地球形状相同的物体:
二、课前检测:1.请写出下列几何体的名称:
[课堂研讨]
新知探究:
1. 由生活中的物体抽象出几何图形,在后面的横线上填上相应的几何体。⑴足球__________ ⑵圆珠笔_________⑶电视机__________⑷花盆__________
⑸漏 斗__________⑹砖 块__________⑺纸箱__________⑻铁 棒__________
范例学习: 1.用自己的语言描述下面这些几何体的特征:
①长方体有______个面,正方体又有_____个面呢? 每个面是_________图形?
②削好的一支铅笔,一部分是_______,另一部分是_______,由此可知圆柱和圆锥的区别就在于圆柱有_______底面,而圆锥只有_______底面,上面是一个_______.
③圆柱和棱柱又有何相同点和不同点呢?
相同点:
不同点:
④圆柱与圆锥的相同点和不同点 网兜和足球的共同体是圆锥吗?
⑤正方体、长方体是不是棱柱呢?
⑥棱柱有_______和_______,本书只讨论_________简称_______
直棱柱和斜棱柱有什么区别?
⑦多面体:
2. 请用多种分类方法把课前检测中的几何体分类,并说明理由。
学习过关:
1.埃及金字塔类似于几何体( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
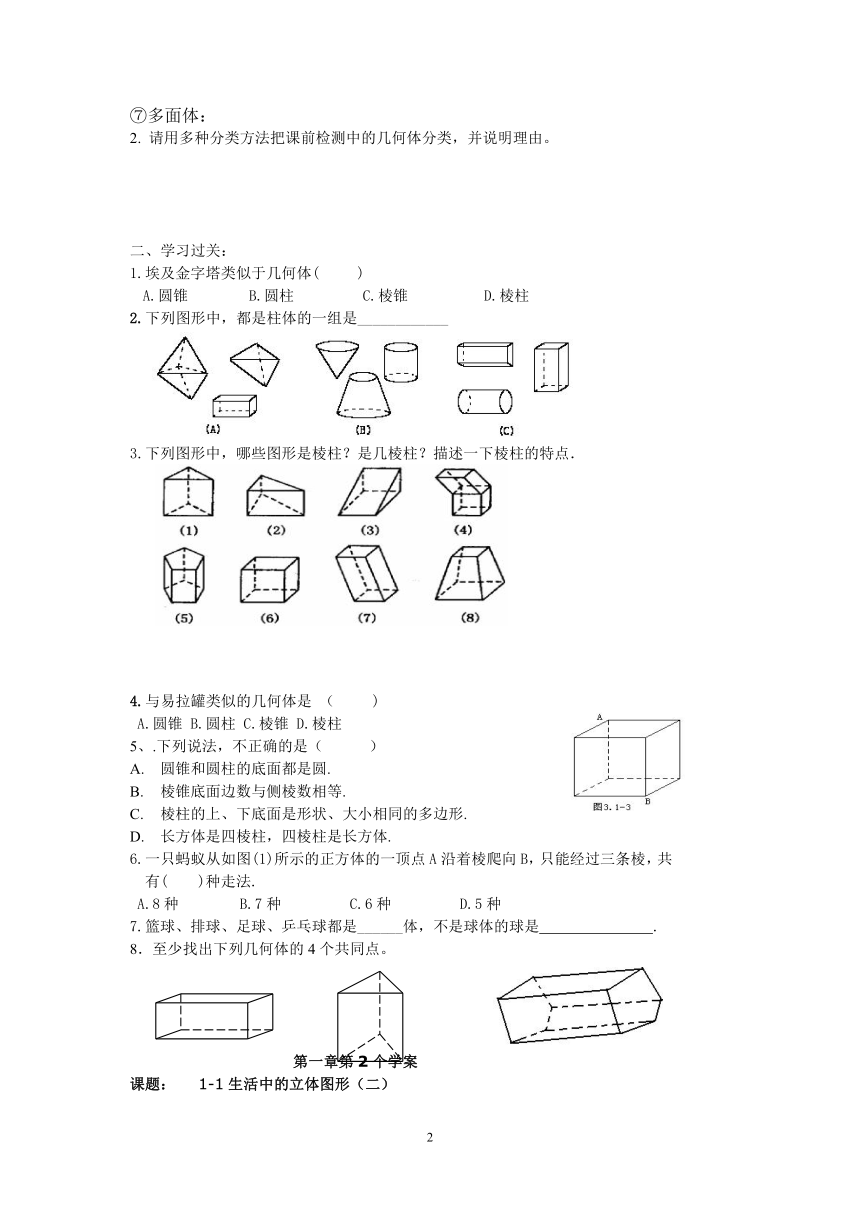
2.下列图形中,都是柱体的一组是____________
3.下列图形中,哪些图形是棱柱?是几棱柱?描述一下棱柱的特点.
4.与易拉罐类似的几何体是 ( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
5、.下列说法,不正确的是( )
圆锥和圆柱的底面都是圆.
棱锥底面边数与侧棱数相等.
棱柱的上、下底面是形状、大小相同的多边形.
长方体是四棱柱,四棱柱是长方体.
6.一只蚂蚁从如图(1)所示的正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有( )种走法.
A.8种 B.7种 C.6种 D.5种
7.篮球、排球、足球、乒乓球都是______体,不是球体的球是 .
8.至少找出下列几何体的4个共同点。
第一章第2个学案
课题: 1-1生活中的立体图形(二)
主备: 审核: 检查:
学习目标:认识点、线、面,初步感受点、线、面之间的关系;进一步经历从现实世界中抽象出图形的过程,从构成图形的基本元素的角度认识常见几何体的某些特征.
学习重点:认识点、线、面,初步感受点、线、面的关系,认识常见几何体的某些特征.
学习难点:认识“点动成线、线动成面、面动成体”和“面与面相交得到线、线与线相交得到点”的事实.
[课前导学]
课前预习:阅读课本P5~7页:完成练习:
(1)观察长方体,在这个图形中,构成它的最基本的元素有____、____、____,你能找出图中的这些基本元素吗?
(2)是不是所有的图形都是由点、线、面构成的呢?你能举一个实例吗?
(3)看课本第5页的上图可知,面可分为________和________.观察该页下面现代化城市的交通图,如果我们将这些公路抽象成线就可以知道线也分为_______和_______两种。
(4)线和线相交可以得到____,如果给出一个几何体,从而有面和面相交可以得到_______。
课前检测:
下图中的几何体由几个面围成?面与面相交成几条线?它们分别是直线段
还是曲线段?
[课堂探讨]
新知探究:
1.长方体有____个面,有____个顶点,过每个顶点有____条棱,长方体共有____条棱。
2.三棱锥是由____个面围成的,有____个顶点,有____条棱。
3.看课本第 8页,我们来完成“想一想”,同学们先经过自己的观察、联想,能发现什么呢?通过对三幅图的观察和描述,我们可以得到一外结论:
点动成________,线动成_________ , _________动成体.请举出一些生活中类似的例子:
范例学习:
下列图形绕虚线旋转一周,能形成一个什么样的几何体.
学习过关:
1.几何图形由_____、_____、_____构成,面有_____面和_____面之分。面与面相交得______,线与线相交得______。点动成_____、线动成_____、面动成_____。
2.长方体是由____个面围成的,圆柱是____个面围成的,球是____个面围成的,圆锥是由__个面围成的,其中围成圆锥的面有_____面,也有____面,圆锥有____条线,___个顶点。
3.图1-1是由( )图形饶虚线旋转一周形成的。
1.图1-2绕虚线旋转一周形成的图形是 ( )
2. 下列说法正确的是 ( )
A.有六条侧棱的棱柱的底面一定是三角形; B.棱锥的侧面是三角形
C.长方体和正方体不是棱柱 D.柱体的上下两底面可以大小不一样
3.下列图形属于棱柱的有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
4. 圆柱,圆锥,球的共同点是_____________________________.
5. 假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________。如果我们把流星看作一个点,那么我们观察流星运动时,会看到它划出一条长弧,这说明_______;当直升飞机起飞后,随着螺旋桨速度的加快,我们会看到一个圆面,这说明________;把一枚硬币用左手竖放在桌面,用右手用力一弹,硬币会高速旋转,我们会看到一个球,这说明_________. 把一块学生使用的三角板以一条直角边为轴旋转一周,所形成的几何体是______。
6.现有一个长为4厘米,宽为3厘米的长方形,得到的几何体是______,这个几何体的体积是________。
7、矩形绕其一边旋转一周形成的几何体叫_______,直角三角形绕其中一个直角边旋转一周形成的几何体叫______.
8、.用6根火柴棒最多可以拼成多少个等边三角形?
第一章第3个学案
课题:1.2展开与折叠(1)
主备: 审核: 检查:
学习目标:模型制作等活动,发展空间观念,积累数学活动经验,在操作活动中,认识常见几何体的某些特征.
学习重点:想象并画出棱柱、棱锥、圆柱、圆锥等简单几何体的表面展开图,能根据表面展开图制作简单的几何体。
学习难点:根据简单几何体的表面展开图折叠成几何体
[课前导学]
一、见P11做一做
1、①这个棱柱的上、下底面是_______(填“相同”或“不同”),它们各有____条边.②这个棱柱有______个侧面,侧面的形状是_________
③侧面的个数与底面的边数的关系是________
④这个棱柱相邻的侧面有______条交线,他们长度之间的关系是__________,他们的数量与上下底面的边数的关系是_____________,侧面与底面有_____条交线,这个棱柱共有___________条交线
⑤线与线相交得______,这个棱柱共有_______个交点
2、在棱柱中①什么是棱_______________________________________
②侧棱:_______________________________ 棱柱的所有侧棱长都_______
③棱柱的上、下底面形状__________,都是________,位置__________
④棱柱、棱锥是怎样命名的?
因此、长方体与正方体都是_________棱柱
⑤什么叫做多面体:
圆柱、圆锥_____________多面体(填是或不是)
二、课前检测:
长方体有___个顶点,___条棱,___个面 ;这些面的形状都是______,那些面的形状完全相同?________________.哪些棱的长度一定相等?__________
[课堂探讨]
新知探究:
1、n棱柱的特征.:有_____个底面,底面形状_________且位置____________,有____条侧棱,有_____条棱, ___个侧面,侧面形状_________,有______个面 ,有_______个顶点,其中,顶点数、面数、与棱数之间的关系为:__________________
2、n棱锥的特征::有___个底面,底面形状_______,有____条侧棱,_____条棱, ___个侧面, 侧面形状_________,有______个面 ,有_______个顶点,其中,顶点数、面数、与棱数之间的关系为:__________________________
3、书中14页想一想
圆柱的侧面展开图为____________,圆柱的表面展开图为____________,
圆锥的侧面展开图为____________,圆锥的表面展开图为____________,
范例学习:
1、①底面为六边形的棱柱,共有____个面,有______个侧面,侧面形状为______,有_______个顶点,________条棱.
②某棱柱有18个顶点,它是________棱柱,有________条棱,_________条侧棱,_________个面,________个侧面,_________个底面。
③某棱柱有15条棱,它是________棱柱,有________个
2、指出下列平面图形是什么几何体的展开图
B
3、(1)图中的图形不是长方体的表面展开图的是( )
(2)思考不是长方体的表面展开图的,如何改动其中一处,使得它是长方体的表面展开图
学习过关: P12页习题1.3知识技能1、2、3, 问题解决1、2,P15页知识技能1。
自我检测:
1、棱柱的侧面都是____形;
2、一个棱柱是十二面体,那么它的底面是___.
3、十棱柱有___个顶点,___条棱,____个面.
4、上、下底面都是五边形的棱柱是___棱柱.
5、一个九棱柱,它的底面边长都是1cm , 侧棱长都是2cm ,则它的侧面积是____.
6、过一个正方体的顶点有____条棱,_____个面
7、一个底面边长是6厘米,侧棱长是5厘米的正六棱柱共有_____条棱,他们的长度和为__________厘米。若沿着一条侧棱将其侧面展成一个平面图形,这个图形的形状是____________?面积是____________?
8、把一个半径为12厘米的半圆围成一个无底的圆锥,求这个圆锥底面圆的半径是多少?
9、将一个无底无盖的圆柱剪开得到一个矩形,其中圆柱的___________等于矩形的一个边长,矩形的另一边长等于_______________.
10、. 用一个宽2 cm,长3 cm的矩形卷成一个圆柱,则此圆柱的侧面积为_______________.体积为__________________
11、指出下列平面图形是什么几何体的展开图
12、说出下列平面图形是否是什么几何体的展开图?
13、在下图的图形中,是三棱柱的侧面展开图的是( )
14、看图,这些图经过折叠可以围成一个棱柱吗?想一想,亲自动手折一折。
15.如图是一多面体的展开图形,每个面都标有字母,请根据要求回答提问:
(1)如果面A在多面体的底部,那么面 在上面;
(2)如果面F在前面,从左面看是面B,则面 在上面;
(3)从右面看面C,面D在后面,面 在上面。
16.下面图形是多面体的平面展开图吗?你能说出这些多面体的名称吗?若不是,请阐述你的理由
17、若一个长方形能折叠成一个所有棱长均相等的五棱柱的侧面,则该长方形的宽与长之比是 。
第一章第4个学案
1.2展开与折叠(2)
主备: 审核: 检查:
学习目标:了解正方体的侧面展开图,并能根据展开图制作成简单的立体模型。
学习重点:亲历探索过程,认识图形“展开与折叠”这一“体一面一体”的过程。
学习难点:判断平面图形围成某种特定图形的可能性。
[课前导学]
课前预习:
阅读课本P13~16页:完成练习:
将一个正方体沿某些棱剪开,展成一个平面图形。然后回答:
(1)你能得到哪些平面图形(画出来)?
(2)能得到图1-4中的平面图形吗?
(3)图1-5中的图形能折叠成一个正方体吗?
课前检测:
1、在下面的图形中,( )是正方体的表面展开图.
2.如下图,哪个是正方体的展开图( )
[课堂探讨] 新知探究:
(1)如果将一个正方体沿某些棱剪开,展成一个平面图形,那么需要剪开______条棱
(2)如何在展开图中找出相对两面?又如何在正方体中找出邻面及对面?
(3)正方体表面展开图有几种?你能得到哪些平面图形(画出来)?
(4)无盖正方体表面展开图有几种?(画出来)?
范例学习:
若一个正方体的两个相对的面上都涂着相同的颜色,那么不可能是这一个正方体的展开图的是( )
学习过关:
1、图中不可以折叠成正方体的是( )
A B C D
2.下图是正方体的展开图,还原成正方体后,其中完全一样的是( )
(1) (2) (3) (4)
A.(1)和(2) B.(1)和(3) C.(2)和(3) D.(3)和(4)
3、如果有一个正方体,它的展开图可能是下面四个展开图中的( )
4、水平放置的正方体的六个面分别用“前面、后面、上面、下面、
左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的
“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则
“祝”、 “你”、 “前”分别表示正方体的__________________.
5、想想看:下面的图形中 是正方体的展开图(只要填序号)。
6、如图,一个3×5的方格纸,现将其剪为三部分,使每一部分都可以折成一个无盖的小方盒,问如何剪?
7.下图是正方体的表面展开图,如果将其合成原来的正方体(右下图)时,与点P重合的两点应该是 ( ) A、S 和 Z B、T 和 Y C、U 和 Y D、T 和 V
8、 将图( 1 )中的图形折叠起来围成一个正方体,应该得到图( 2 )中的( )
9、魔方由27个小正方体组成,我们知道魔方各方面颜色均不同,请问这27个小正方体中,没有涂色的、涂一种颜色的、涂两种颜色的、涂三种颜色的各有多少个
10.在下列正方体的展开中,确定点M、N的位置。
第一章第5个学案
截一个几何体
主备: 审核: 检查:
学习目标:经历观察用平面截一个正方体,猜想截面的形状,实际操作、验证,推理等数学活动过程,丰富对空间图形的几何直觉,激发形象思维.
学习重点:参与用一个平面截一个正方体的数学活动,体会截面和几何体的关系。
学习难点:体会几何体在切截过程中的变化,在面与体的转换中发展空间观念.
[课前导学]
课前预习:阅读课本P17~18页:完成练习:
(1)将一个长方体切一刀观察截出的面是什么形状,再换一种切法,看能否截出不同形状的面?下面是几种不同的切法,请你观察截面的形状分别是什么?
(2)判断题:
1.用一个平面去截一个正方体,截出的面一定是正方形或长方形. ( )
2.用一个平面去截一个圆柱,截出的面一定是圆. ( )
3.用一个平面去截圆锥,截出的面一定是三角形. ( )
4.用一个平面去截一个球,无论如何截,截面都是一个圆.( )
课前检测:
1.用一个平面去截圆锥,得到的平面不可能是( )
2.用一个平面去截一个圆柱,得到的图形不可能是( )
3. 指出下列几何体的截面形状.
[课堂探讨] 新知探究:
用平面截下列几何体,找出相应的截面形状.
(1)
(2)
(3)
范例学习:
1. 用平面去截一个正方体,截面的形状可能有哪些?请写出来,并一一画出。
2.用平面去截以下几何体,截面形状有可能是哪些图形?
几何体 截面形状
正方体
圆 柱
圆 锥
球
学习过关:
1.下面几何体中,截面图形不可能是圆的是( )
A.圆柱 B.圆锥 C.球 D.正方体
2.用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是________。
3.用一个平面去截五棱柱,边数最多的截面是_______形.
4.用平面去截一个正方体,能得到一个等边三角形吗?能截到一个直角三角形或钝角三角形截面吗?
5、有下列几何体:(1)圆柱;(2)正方体;(3)棱柱;(4)球;(5)圆锥;(6)长方体。则这些几何体中截面可能是圆的有( )
A、2种 B、3种 C、4种 D、5种
4、正方体被一个平面所截,所得边数最多的多边形是( )
A、四边形 B、五边形 C、六边形 D、七边形
5、用一个平面截圆柱,则截面形状不可能是( )
A.圆 B.正方体 . C长方体 D.梯形
6、用一个平面截正方体,若所得的截面是一个三角形,则留下的较大的一块几何体一定有 ( )
A.7个面 B.15条棱 C.7个顶点 D.10个顶点
7、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?
8、在一个圆柱体中你能用一个平面截出一个三角形吗?能截出一个半圆吗?在什么条件下,你能截出一个正方形?
9、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如截面是三角形呢?
10、到菜市场买一块长方体形状的豆腐,你能只用三刀将其切成八块吗?试试看.
第一章第6个学案
1.4从不同方向看(1)
主备: 审核: 检查:
学习目标:在观察的过程中初步体会从不同方向观察物体可能看到不同的图形,能识别简单物体的三视图,发展空间观念。
学习重点:体会从不同方向观察同一物体可能看到的不同的图形,并能识别简单的三视图。
学习难点:识别简单的三视图。
[课前导学] 课前预习 阅读课本P20~22页:完成练习:
(1)甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是( )A.甲在丁的对面,乙在甲的左边,丙在丁的右边B.丙在乙的对面,丙的左边是甲,右边是乙C.甲在乙的对面,甲的右边是丙,左边是丁D.甲在丁的对面,乙在甲的右边,丙在丁的右边
(2)如下图,看东西时当我们从正面看就得到_________;从左面看就得到_________;从上面看就得到_________。
课前检测:
桌子上放着一个长方体和圆柱(如下图),说出下列三幅图分别是哪种视图.
[课堂探讨] 新知探究:
画出右边几何体的主视图、左视图和俯视图.
范例学习:
根据以下几何体,分别画出它们的三视图.
学习过关:
1.圆柱的俯视图是_______,主视图是_________.
2.主视图,左视图和俯视图都一样的几何体有________(写出一种即可).
3、 圆锥的三视图是( )
A. 主视图和俯视图是三角形,侧视图是圆。
B. 主视图和侧视图是三角形,俯视图是圆。
C. 主视图和侧视图是三角形,俯视图是圆和圆心。
D. 主视图和俯视图是三角形,侧视图是圆和圆心。
4.有一辆小汽车,小红从空中往下看这辆小汽车,图____是小红看到的形状.
5、画出一个三棱锥的三视图:
7、一个几何体的主视图,左视图和俯视图如下,请想一想这是一个什么几何体 请画一个草图表示.
主视图 俯视图 左视图
8、有一个正方体,在它的各个面上分别标上字母A、B、C、D、E、F,甲、乙、丙三位同学从不同的方向去观察其正方体,观察结果如图所示.问这个正方体各个面上的字母对面各是什么字母?
9、如图所示的积木是由16块棱长为1cm的正方体堆积而成的,请求出它们的表面积.
第一章第7个学案
1.4从不同方向看(2)
主备: 审核: 检查:
学习目标:会观察由小立方块组成的不同的几何体,并画出三视图,同时能根据每个位置的小立方块的个数及其中一种视图画出另外两种视图.
学习重点:通过小立方块搭建几何体的俯视图及相应位置上方块的个数,画出这个几何体的主视图和左视图.
学习难点:由已知搭建的几何体的俯视图及相应位置上的小立方块的个数画出这个几何体的主视图和左视图.
[课前导学]
课前预习: 阅读课本P25~26页 : 完成练习:
下图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.
[课堂探讨] 范例学习:
1.如图是由几个小立方体块所搭几何体的俯视图,小正方形中的数字表示在该位置小立块的个数,请画出这个几何体的主视图和左视图。
2.如图是由一些相同的小正方体构成的立体图形的三种视图构成这个立体图形的小正方体的个数是( ) A.3 B.4 C.5 D.6
3.用小立方块搭一个几何体,使得它的主视图和俯视图如图所示。这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
学习过关:
1. 如图这是一个由小立方块搭成的几何体的俯视图,小正方形中得数字表示在该位置的小立方块的个数,请你分别画出它们的主视图与左视图.
2. 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( ) A.5 B.6 C.7 D.8
3、 用小立方块搭一几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中的字母表示在该位置小立方块的个数,请问:
(1)a,b,c各表示几?
(2)这个几何体最少由几个小正方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体的左视图.
4、用小立方块搭一个几何体,使得它的主视图和俯视图如图所示。则最多____块,最少_____块.
第一章第8个学案
1.5生活中的平面图形
主备: 审核: 检查:
学习目标:经历从现实世界中抽象出平面图形的过程,在具体情境中认识多边形、扇形,在丰富的活动中发展有条理的思考。
学习重点:经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩。
学习难点:在丰富的活动中发展有条理的思考。
[课前导学] 课前预习:阅读课本P28~30页:完成练习:
(1)多边形(三角形、四边形、五边形等)都是由不在同一条直线上的线段_____________而成的图形,这些都是直线型的图形。
圆上两点之间的部分叫做_________,由一条弧和经过这条弧端点的两条半径组成的图形叫做__________。
(2)写出几个你熟悉的四边形的名称 。
(3)一个六边形,从它的顶点出发,分别连结这个顶点和其他各顶点,可以把这个六边形分割成 个三角形。
(4)如图,有 个四边形。
课前检测:
1、如图,从一个多边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成若干个三角形.
(1)根据图甲的方法,把图乙的七边形分割成若干个三角形;
(2)按图甲的方法,十二边形可以分割成几个三角形(只要求写出答案)
2、如右图,图中的三角形的个数为___________。
[课堂探讨] 新知探究:
对于一个多边形,从它的一个顶点出发,分别连结这个顶点和其余各顶点,可以将这个多边形分割成若干个三角形。也可以在多边形内任意取一点,将这点与多边形的各顶点相连,这样也可以将这个多边形分割成若干个三角形。(如图)
一般地,对于一个n边形,从一个顶点出发连线分割,可以得到__________个三角形(如左图);从n边形内部一点与各顶点连线分割,可以得到___________个三角形(如中图)。;从n边形边上一点与各顶点连线分割,可以得到___________个三角形(如右图)。
范例学习: 观察下列图形,
(1)第一个图形有1个三角形,第二个图形有 个三角形,第三个图形有 个三角形;第四个图形有 个三角形,
(2)以此类推,第5图形应该有 三角形。
学习过关:
1、判断题
(1)扇形是圆的一部分. ( )
(2)圆的一部分是扇形. ( )
(3)扇形的周长等于它的弧长.( )
2、如图,图中有_______个三角形,有______个四边形.
3、如图,请你指出图中有多少个的正方形,多少个三角形?
第2题 第3题 第4题
4、如图,圆O上有不同的三个点A、B、C,它们可以构成多少个不同的弧?多少个不同的扇形?
5、长方形被切去一刀,得到多少种不同的多边形?请一一画出来。
6、用从一个顶点出发,分别连结这个顶点和其余各顶点的方法把图形分割成三角形,可以分割成5个三角形的多边形是( )
A、五边形 B、六边形 C、七边形 D、八边形
7、如右图,图中共有正方形( )
A、12个 B、13个 C、15个 D、18个
3、已知一个圆,任意画出它的三条半径,能得到( )个扇形.
A、4 B、5 C、6 D、8
⑴
⑵
⑶
⑷
程
前
你
祝
似
锦
(第4题)
PAGE
18
课题: 1-1生活中的立体图形(一)
主备: 审核: 检查:
学习目标:在具体的情境中,认识并能够辨别出基本的几何体。
通过比较,学会观察物体间的特征,体会几何体间的联系和区别,并能根据几何体的特征,对其进行简单分类。
学习重点:认识一些基本的几何体,并能描述这些几何体的特征。
学习难点:描述几何体的特征,对几何体进行分类。
[课前导学]
一、课前预习:阅读课本P1~4页:完成练习:
课本第1页的彩图中,我们在欣赏这个城市的美景时,不妨用数学的眼光观察一下,这个美丽的城市也是我们数学世界——丰富的图形世界,你能从中发现哪些熟悉的图形?
(1)广场中心的喷泉池是________形,大楼是_________体。
(2)从不同的方向观察同一建筑物,看到的图形是______(A、一样的 B、不一样的.)
课本第2页的彩图中,映人我们眼帘的便是各式各样的立体图形,请看图识几何体:
(3)发现了亭子的顶端是__________体,下面的支柱是_________体.
(4)人民大会堂中间的建筑是________体.
(5)从太空看地球是________体。举例说明与地球形状相同的物体:
二、课前检测:1.请写出下列几何体的名称:
[课堂研讨]
新知探究:
1. 由生活中的物体抽象出几何图形,在后面的横线上填上相应的几何体。⑴足球__________ ⑵圆珠笔_________⑶电视机__________⑷花盆__________
⑸漏 斗__________⑹砖 块__________⑺纸箱__________⑻铁 棒__________
范例学习: 1.用自己的语言描述下面这些几何体的特征:
①长方体有______个面,正方体又有_____个面呢? 每个面是_________图形?
②削好的一支铅笔,一部分是_______,另一部分是_______,由此可知圆柱和圆锥的区别就在于圆柱有_______底面,而圆锥只有_______底面,上面是一个_______.
③圆柱和棱柱又有何相同点和不同点呢?
相同点:
不同点:
④圆柱与圆锥的相同点和不同点 网兜和足球的共同体是圆锥吗?
⑤正方体、长方体是不是棱柱呢?
⑥棱柱有_______和_______,本书只讨论_________简称_______
直棱柱和斜棱柱有什么区别?
⑦多面体:
2. 请用多种分类方法把课前检测中的几何体分类,并说明理由。
学习过关:
1.埃及金字塔类似于几何体( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
2.下列图形中,都是柱体的一组是____________
3.下列图形中,哪些图形是棱柱?是几棱柱?描述一下棱柱的特点.
4.与易拉罐类似的几何体是 ( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
5、.下列说法,不正确的是( )
圆锥和圆柱的底面都是圆.
棱锥底面边数与侧棱数相等.
棱柱的上、下底面是形状、大小相同的多边形.
长方体是四棱柱,四棱柱是长方体.
6.一只蚂蚁从如图(1)所示的正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有( )种走法.
A.8种 B.7种 C.6种 D.5种
7.篮球、排球、足球、乒乓球都是______体,不是球体的球是 .
8.至少找出下列几何体的4个共同点。
第一章第2个学案
课题: 1-1生活中的立体图形(二)
主备: 审核: 检查:
学习目标:认识点、线、面,初步感受点、线、面之间的关系;进一步经历从现实世界中抽象出图形的过程,从构成图形的基本元素的角度认识常见几何体的某些特征.
学习重点:认识点、线、面,初步感受点、线、面的关系,认识常见几何体的某些特征.
学习难点:认识“点动成线、线动成面、面动成体”和“面与面相交得到线、线与线相交得到点”的事实.
[课前导学]
课前预习:阅读课本P5~7页:完成练习:
(1)观察长方体,在这个图形中,构成它的最基本的元素有____、____、____,你能找出图中的这些基本元素吗?
(2)是不是所有的图形都是由点、线、面构成的呢?你能举一个实例吗?
(3)看课本第5页的上图可知,面可分为________和________.观察该页下面现代化城市的交通图,如果我们将这些公路抽象成线就可以知道线也分为_______和_______两种。
(4)线和线相交可以得到____,如果给出一个几何体,从而有面和面相交可以得到_______。
课前检测:
下图中的几何体由几个面围成?面与面相交成几条线?它们分别是直线段
还是曲线段?
[课堂探讨]
新知探究:
1.长方体有____个面,有____个顶点,过每个顶点有____条棱,长方体共有____条棱。
2.三棱锥是由____个面围成的,有____个顶点,有____条棱。
3.看课本第 8页,我们来完成“想一想”,同学们先经过自己的观察、联想,能发现什么呢?通过对三幅图的观察和描述,我们可以得到一外结论:
点动成________,线动成_________ , _________动成体.请举出一些生活中类似的例子:
范例学习:
下列图形绕虚线旋转一周,能形成一个什么样的几何体.
学习过关:
1.几何图形由_____、_____、_____构成,面有_____面和_____面之分。面与面相交得______,线与线相交得______。点动成_____、线动成_____、面动成_____。
2.长方体是由____个面围成的,圆柱是____个面围成的,球是____个面围成的,圆锥是由__个面围成的,其中围成圆锥的面有_____面,也有____面,圆锥有____条线,___个顶点。
3.图1-1是由( )图形饶虚线旋转一周形成的。
1.图1-2绕虚线旋转一周形成的图形是 ( )
2. 下列说法正确的是 ( )
A.有六条侧棱的棱柱的底面一定是三角形; B.棱锥的侧面是三角形
C.长方体和正方体不是棱柱 D.柱体的上下两底面可以大小不一样
3.下列图形属于棱柱的有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
4. 圆柱,圆锥,球的共同点是_____________________________.
5. 假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________。如果我们把流星看作一个点,那么我们观察流星运动时,会看到它划出一条长弧,这说明_______;当直升飞机起飞后,随着螺旋桨速度的加快,我们会看到一个圆面,这说明________;把一枚硬币用左手竖放在桌面,用右手用力一弹,硬币会高速旋转,我们会看到一个球,这说明_________. 把一块学生使用的三角板以一条直角边为轴旋转一周,所形成的几何体是______。
6.现有一个长为4厘米,宽为3厘米的长方形,得到的几何体是______,这个几何体的体积是________。
7、矩形绕其一边旋转一周形成的几何体叫_______,直角三角形绕其中一个直角边旋转一周形成的几何体叫______.
8、.用6根火柴棒最多可以拼成多少个等边三角形?
第一章第3个学案
课题:1.2展开与折叠(1)
主备: 审核: 检查:
学习目标:模型制作等活动,发展空间观念,积累数学活动经验,在操作活动中,认识常见几何体的某些特征.
学习重点:想象并画出棱柱、棱锥、圆柱、圆锥等简单几何体的表面展开图,能根据表面展开图制作简单的几何体。
学习难点:根据简单几何体的表面展开图折叠成几何体
[课前导学]
一、见P11做一做
1、①这个棱柱的上、下底面是_______(填“相同”或“不同”),它们各有____条边.②这个棱柱有______个侧面,侧面的形状是_________
③侧面的个数与底面的边数的关系是________
④这个棱柱相邻的侧面有______条交线,他们长度之间的关系是__________,他们的数量与上下底面的边数的关系是_____________,侧面与底面有_____条交线,这个棱柱共有___________条交线
⑤线与线相交得______,这个棱柱共有_______个交点
2、在棱柱中①什么是棱_______________________________________
②侧棱:_______________________________ 棱柱的所有侧棱长都_______
③棱柱的上、下底面形状__________,都是________,位置__________
④棱柱、棱锥是怎样命名的?
因此、长方体与正方体都是_________棱柱
⑤什么叫做多面体:
圆柱、圆锥_____________多面体(填是或不是)
二、课前检测:
长方体有___个顶点,___条棱,___个面 ;这些面的形状都是______,那些面的形状完全相同?________________.哪些棱的长度一定相等?__________
[课堂探讨]
新知探究:
1、n棱柱的特征.:有_____个底面,底面形状_________且位置____________,有____条侧棱,有_____条棱, ___个侧面,侧面形状_________,有______个面 ,有_______个顶点,其中,顶点数、面数、与棱数之间的关系为:__________________
2、n棱锥的特征::有___个底面,底面形状_______,有____条侧棱,_____条棱, ___个侧面, 侧面形状_________,有______个面 ,有_______个顶点,其中,顶点数、面数、与棱数之间的关系为:__________________________
3、书中14页想一想
圆柱的侧面展开图为____________,圆柱的表面展开图为____________,
圆锥的侧面展开图为____________,圆锥的表面展开图为____________,
范例学习:
1、①底面为六边形的棱柱,共有____个面,有______个侧面,侧面形状为______,有_______个顶点,________条棱.
②某棱柱有18个顶点,它是________棱柱,有________条棱,_________条侧棱,_________个面,________个侧面,_________个底面。
③某棱柱有15条棱,它是________棱柱,有________个
2、指出下列平面图形是什么几何体的展开图
B
3、(1)图中的图形不是长方体的表面展开图的是( )
(2)思考不是长方体的表面展开图的,如何改动其中一处,使得它是长方体的表面展开图
学习过关: P12页习题1.3知识技能1、2、3, 问题解决1、2,P15页知识技能1。
自我检测:
1、棱柱的侧面都是____形;
2、一个棱柱是十二面体,那么它的底面是___.
3、十棱柱有___个顶点,___条棱,____个面.
4、上、下底面都是五边形的棱柱是___棱柱.
5、一个九棱柱,它的底面边长都是1cm , 侧棱长都是2cm ,则它的侧面积是____.
6、过一个正方体的顶点有____条棱,_____个面
7、一个底面边长是6厘米,侧棱长是5厘米的正六棱柱共有_____条棱,他们的长度和为__________厘米。若沿着一条侧棱将其侧面展成一个平面图形,这个图形的形状是____________?面积是____________?
8、把一个半径为12厘米的半圆围成一个无底的圆锥,求这个圆锥底面圆的半径是多少?
9、将一个无底无盖的圆柱剪开得到一个矩形,其中圆柱的___________等于矩形的一个边长,矩形的另一边长等于_______________.
10、. 用一个宽2 cm,长3 cm的矩形卷成一个圆柱,则此圆柱的侧面积为_______________.体积为__________________
11、指出下列平面图形是什么几何体的展开图
12、说出下列平面图形是否是什么几何体的展开图?
13、在下图的图形中,是三棱柱的侧面展开图的是( )
14、看图,这些图经过折叠可以围成一个棱柱吗?想一想,亲自动手折一折。
15.如图是一多面体的展开图形,每个面都标有字母,请根据要求回答提问:
(1)如果面A在多面体的底部,那么面 在上面;
(2)如果面F在前面,从左面看是面B,则面 在上面;
(3)从右面看面C,面D在后面,面 在上面。
16.下面图形是多面体的平面展开图吗?你能说出这些多面体的名称吗?若不是,请阐述你的理由
17、若一个长方形能折叠成一个所有棱长均相等的五棱柱的侧面,则该长方形的宽与长之比是 。
第一章第4个学案
1.2展开与折叠(2)
主备: 审核: 检查:
学习目标:了解正方体的侧面展开图,并能根据展开图制作成简单的立体模型。
学习重点:亲历探索过程,认识图形“展开与折叠”这一“体一面一体”的过程。
学习难点:判断平面图形围成某种特定图形的可能性。
[课前导学]
课前预习:
阅读课本P13~16页:完成练习:
将一个正方体沿某些棱剪开,展成一个平面图形。然后回答:
(1)你能得到哪些平面图形(画出来)?
(2)能得到图1-4中的平面图形吗?
(3)图1-5中的图形能折叠成一个正方体吗?
课前检测:
1、在下面的图形中,( )是正方体的表面展开图.
2.如下图,哪个是正方体的展开图( )
[课堂探讨] 新知探究:
(1)如果将一个正方体沿某些棱剪开,展成一个平面图形,那么需要剪开______条棱
(2)如何在展开图中找出相对两面?又如何在正方体中找出邻面及对面?
(3)正方体表面展开图有几种?你能得到哪些平面图形(画出来)?
(4)无盖正方体表面展开图有几种?(画出来)?
范例学习:
若一个正方体的两个相对的面上都涂着相同的颜色,那么不可能是这一个正方体的展开图的是( )
学习过关:
1、图中不可以折叠成正方体的是( )
A B C D
2.下图是正方体的展开图,还原成正方体后,其中完全一样的是( )
(1) (2) (3) (4)
A.(1)和(2) B.(1)和(3) C.(2)和(3) D.(3)和(4)
3、如果有一个正方体,它的展开图可能是下面四个展开图中的( )
4、水平放置的正方体的六个面分别用“前面、后面、上面、下面、
左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的
“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则
“祝”、 “你”、 “前”分别表示正方体的__________________.
5、想想看:下面的图形中 是正方体的展开图(只要填序号)。
6、如图,一个3×5的方格纸,现将其剪为三部分,使每一部分都可以折成一个无盖的小方盒,问如何剪?
7.下图是正方体的表面展开图,如果将其合成原来的正方体(右下图)时,与点P重合的两点应该是 ( ) A、S 和 Z B、T 和 Y C、U 和 Y D、T 和 V
8、 将图( 1 )中的图形折叠起来围成一个正方体,应该得到图( 2 )中的( )
9、魔方由27个小正方体组成,我们知道魔方各方面颜色均不同,请问这27个小正方体中,没有涂色的、涂一种颜色的、涂两种颜色的、涂三种颜色的各有多少个
10.在下列正方体的展开中,确定点M、N的位置。
第一章第5个学案
截一个几何体
主备: 审核: 检查:
学习目标:经历观察用平面截一个正方体,猜想截面的形状,实际操作、验证,推理等数学活动过程,丰富对空间图形的几何直觉,激发形象思维.
学习重点:参与用一个平面截一个正方体的数学活动,体会截面和几何体的关系。
学习难点:体会几何体在切截过程中的变化,在面与体的转换中发展空间观念.
[课前导学]
课前预习:阅读课本P17~18页:完成练习:
(1)将一个长方体切一刀观察截出的面是什么形状,再换一种切法,看能否截出不同形状的面?下面是几种不同的切法,请你观察截面的形状分别是什么?
(2)判断题:
1.用一个平面去截一个正方体,截出的面一定是正方形或长方形. ( )
2.用一个平面去截一个圆柱,截出的面一定是圆. ( )
3.用一个平面去截圆锥,截出的面一定是三角形. ( )
4.用一个平面去截一个球,无论如何截,截面都是一个圆.( )
课前检测:
1.用一个平面去截圆锥,得到的平面不可能是( )
2.用一个平面去截一个圆柱,得到的图形不可能是( )
3. 指出下列几何体的截面形状.
[课堂探讨] 新知探究:
用平面截下列几何体,找出相应的截面形状.
(1)
(2)
(3)
范例学习:
1. 用平面去截一个正方体,截面的形状可能有哪些?请写出来,并一一画出。
2.用平面去截以下几何体,截面形状有可能是哪些图形?
几何体 截面形状
正方体
圆 柱
圆 锥
球
学习过关:
1.下面几何体中,截面图形不可能是圆的是( )
A.圆柱 B.圆锥 C.球 D.正方体
2.用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是________。
3.用一个平面去截五棱柱,边数最多的截面是_______形.
4.用平面去截一个正方体,能得到一个等边三角形吗?能截到一个直角三角形或钝角三角形截面吗?
5、有下列几何体:(1)圆柱;(2)正方体;(3)棱柱;(4)球;(5)圆锥;(6)长方体。则这些几何体中截面可能是圆的有( )
A、2种 B、3种 C、4种 D、5种
4、正方体被一个平面所截,所得边数最多的多边形是( )
A、四边形 B、五边形 C、六边形 D、七边形
5、用一个平面截圆柱,则截面形状不可能是( )
A.圆 B.正方体 . C长方体 D.梯形
6、用一个平面截正方体,若所得的截面是一个三角形,则留下的较大的一块几何体一定有 ( )
A.7个面 B.15条棱 C.7个顶点 D.10个顶点
7、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?
8、在一个圆柱体中你能用一个平面截出一个三角形吗?能截出一个半圆吗?在什么条件下,你能截出一个正方形?
9、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如截面是三角形呢?
10、到菜市场买一块长方体形状的豆腐,你能只用三刀将其切成八块吗?试试看.
第一章第6个学案
1.4从不同方向看(1)
主备: 审核: 检查:
学习目标:在观察的过程中初步体会从不同方向观察物体可能看到不同的图形,能识别简单物体的三视图,发展空间观念。
学习重点:体会从不同方向观察同一物体可能看到的不同的图形,并能识别简单的三视图。
学习难点:识别简单的三视图。
[课前导学] 课前预习 阅读课本P20~22页:完成练习:
(1)甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是( )A.甲在丁的对面,乙在甲的左边,丙在丁的右边B.丙在乙的对面,丙的左边是甲,右边是乙C.甲在乙的对面,甲的右边是丙,左边是丁D.甲在丁的对面,乙在甲的右边,丙在丁的右边
(2)如下图,看东西时当我们从正面看就得到_________;从左面看就得到_________;从上面看就得到_________。
课前检测:
桌子上放着一个长方体和圆柱(如下图),说出下列三幅图分别是哪种视图.
[课堂探讨] 新知探究:
画出右边几何体的主视图、左视图和俯视图.
范例学习:
根据以下几何体,分别画出它们的三视图.
学习过关:
1.圆柱的俯视图是_______,主视图是_________.
2.主视图,左视图和俯视图都一样的几何体有________(写出一种即可).
3、 圆锥的三视图是( )
A. 主视图和俯视图是三角形,侧视图是圆。
B. 主视图和侧视图是三角形,俯视图是圆。
C. 主视图和侧视图是三角形,俯视图是圆和圆心。
D. 主视图和俯视图是三角形,侧视图是圆和圆心。
4.有一辆小汽车,小红从空中往下看这辆小汽车,图____是小红看到的形状.
5、画出一个三棱锥的三视图:
7、一个几何体的主视图,左视图和俯视图如下,请想一想这是一个什么几何体 请画一个草图表示.
主视图 俯视图 左视图
8、有一个正方体,在它的各个面上分别标上字母A、B、C、D、E、F,甲、乙、丙三位同学从不同的方向去观察其正方体,观察结果如图所示.问这个正方体各个面上的字母对面各是什么字母?
9、如图所示的积木是由16块棱长为1cm的正方体堆积而成的,请求出它们的表面积.
第一章第7个学案
1.4从不同方向看(2)
主备: 审核: 检查:
学习目标:会观察由小立方块组成的不同的几何体,并画出三视图,同时能根据每个位置的小立方块的个数及其中一种视图画出另外两种视图.
学习重点:通过小立方块搭建几何体的俯视图及相应位置上方块的个数,画出这个几何体的主视图和左视图.
学习难点:由已知搭建的几何体的俯视图及相应位置上的小立方块的个数画出这个几何体的主视图和左视图.
[课前导学]
课前预习: 阅读课本P25~26页 : 完成练习:
下图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.
[课堂探讨] 范例学习:
1.如图是由几个小立方体块所搭几何体的俯视图,小正方形中的数字表示在该位置小立块的个数,请画出这个几何体的主视图和左视图。
2.如图是由一些相同的小正方体构成的立体图形的三种视图构成这个立体图形的小正方体的个数是( ) A.3 B.4 C.5 D.6
3.用小立方块搭一个几何体,使得它的主视图和俯视图如图所示。这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
学习过关:
1. 如图这是一个由小立方块搭成的几何体的俯视图,小正方形中得数字表示在该位置的小立方块的个数,请你分别画出它们的主视图与左视图.
2. 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( ) A.5 B.6 C.7 D.8
3、 用小立方块搭一几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中的字母表示在该位置小立方块的个数,请问:
(1)a,b,c各表示几?
(2)这个几何体最少由几个小正方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体的左视图.
4、用小立方块搭一个几何体,使得它的主视图和俯视图如图所示。则最多____块,最少_____块.
第一章第8个学案
1.5生活中的平面图形
主备: 审核: 检查:
学习目标:经历从现实世界中抽象出平面图形的过程,在具体情境中认识多边形、扇形,在丰富的活动中发展有条理的思考。
学习重点:经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩。
学习难点:在丰富的活动中发展有条理的思考。
[课前导学] 课前预习:阅读课本P28~30页:完成练习:
(1)多边形(三角形、四边形、五边形等)都是由不在同一条直线上的线段_____________而成的图形,这些都是直线型的图形。
圆上两点之间的部分叫做_________,由一条弧和经过这条弧端点的两条半径组成的图形叫做__________。
(2)写出几个你熟悉的四边形的名称 。
(3)一个六边形,从它的顶点出发,分别连结这个顶点和其他各顶点,可以把这个六边形分割成 个三角形。
(4)如图,有 个四边形。
课前检测:
1、如图,从一个多边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成若干个三角形.
(1)根据图甲的方法,把图乙的七边形分割成若干个三角形;
(2)按图甲的方法,十二边形可以分割成几个三角形(只要求写出答案)
2、如右图,图中的三角形的个数为___________。
[课堂探讨] 新知探究:
对于一个多边形,从它的一个顶点出发,分别连结这个顶点和其余各顶点,可以将这个多边形分割成若干个三角形。也可以在多边形内任意取一点,将这点与多边形的各顶点相连,这样也可以将这个多边形分割成若干个三角形。(如图)
一般地,对于一个n边形,从一个顶点出发连线分割,可以得到__________个三角形(如左图);从n边形内部一点与各顶点连线分割,可以得到___________个三角形(如中图)。;从n边形边上一点与各顶点连线分割,可以得到___________个三角形(如右图)。
范例学习: 观察下列图形,
(1)第一个图形有1个三角形,第二个图形有 个三角形,第三个图形有 个三角形;第四个图形有 个三角形,
(2)以此类推,第5图形应该有 三角形。
学习过关:
1、判断题
(1)扇形是圆的一部分. ( )
(2)圆的一部分是扇形. ( )
(3)扇形的周长等于它的弧长.( )
2、如图,图中有_______个三角形,有______个四边形.
3、如图,请你指出图中有多少个的正方形,多少个三角形?
第2题 第3题 第4题
4、如图,圆O上有不同的三个点A、B、C,它们可以构成多少个不同的弧?多少个不同的扇形?
5、长方形被切去一刀,得到多少种不同的多边形?请一一画出来。
6、用从一个顶点出发,分别连结这个顶点和其余各顶点的方法把图形分割成三角形,可以分割成5个三角形的多边形是( )
A、五边形 B、六边形 C、七边形 D、八边形
7、如右图,图中共有正方形( )
A、12个 B、13个 C、15个 D、18个
3、已知一个圆,任意画出它的三条半径,能得到( )个扇形.
A、4 B、5 C、6 D、8
⑴
⑵
⑶
⑷
程
前
你
祝
似
锦
(第4题)
PAGE
18
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
