一元二次方程（1）

(共16张PPT)
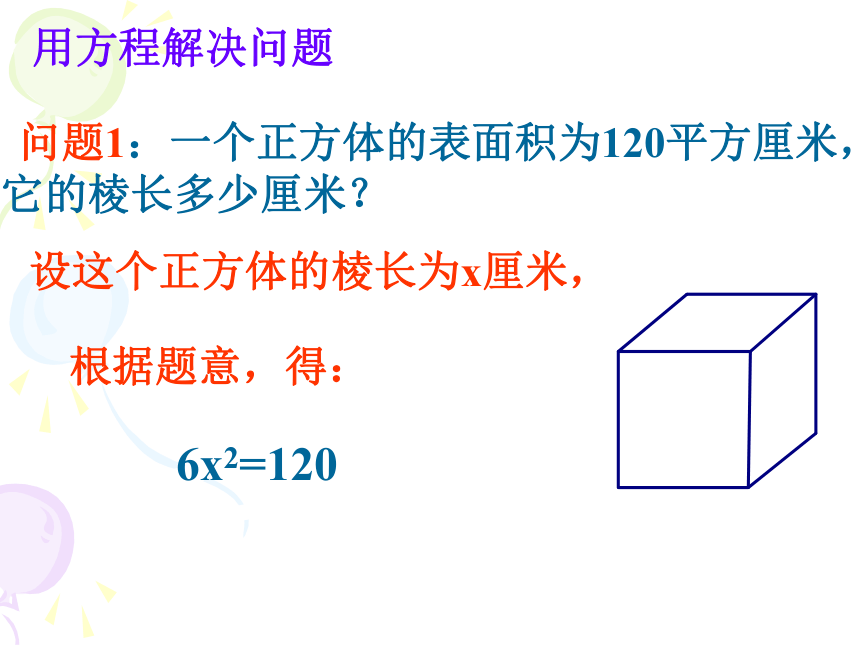
问题1：一个正方体的表面积为120平方厘米，它的棱长多少厘米？
设这个正方体的棱长为x厘米，
根据题意，得：
6x2=120
用方程解决问题
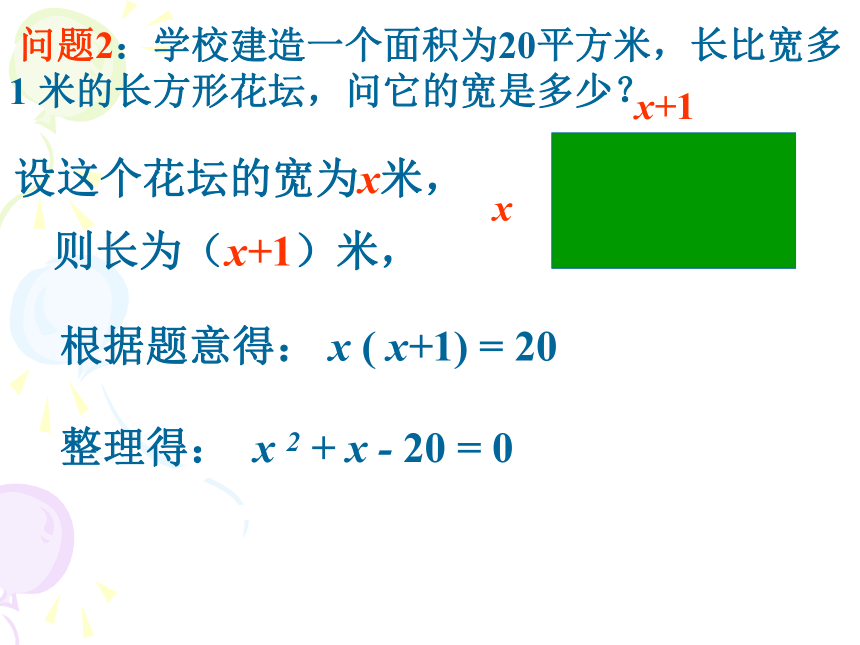
问题2：学校建造一个面积为20平方米，长比宽多 1 米的长方形花坛，问它的宽是多少？
x
x+1
设这个花坛的宽为x米，
则长为（x+1）米，
根据题意得： x ( x+1) = 20
整理得： x 2 + x - 20 = 0
有一张矩形纸片，长25cm，宽15cm，在它的四角各剪去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒.
问题3：
15㎝
x
25㎝
300cm2
如果要制作的无盖方盒的底面积为300cm2，那么纸片各角应剪去的正方形边长为多少cm？
(25-2x)
(15-2x)
（25－2x）（15－2x）=300
去括号、移项、合并同类项得：
4x2 – 80x+75=0 ②
设剪去正方形边长为x，根据题意得：
①
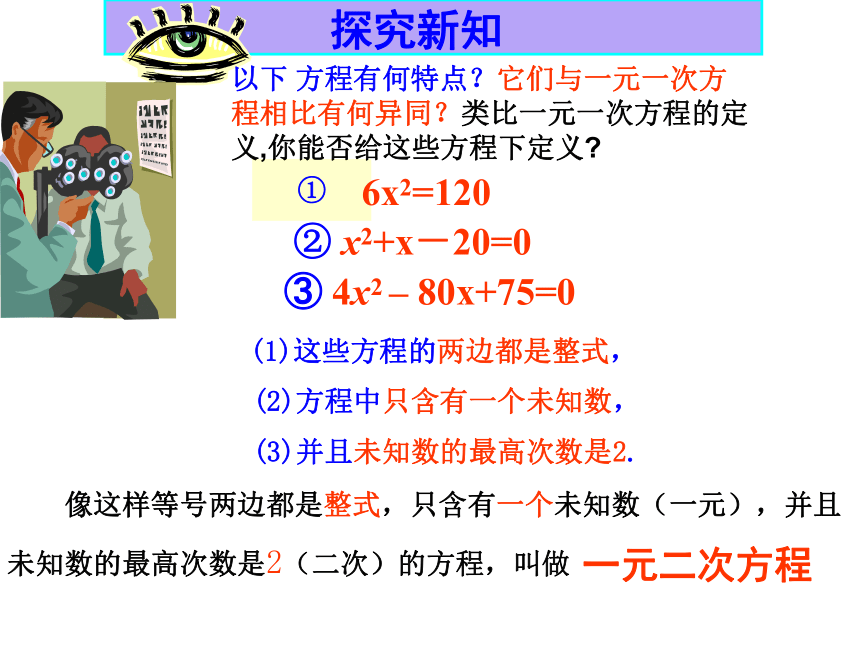
以下 方程有何特点？它们与一元一次方程相比有何异同？类比一元一次方程的定义,你能否给这些方程下定义
　　像这样等号两边都是整式，只含有一个未知数（一元），并且
未知数的最高次数是2（二次）的方程，叫做
② x2+x－20=0
(1)这些方程的两边都是整式，
(2)方程中只含有一个未知数，
(3)并且未知数的最高次数是2.
探究新知
③ 4x2 – 80x+75=0
一元二次方程
6x2=120
判断下列方程是否为一元二次方程？
(1)x2+x – 36=0
(2) x3+ x2- 36=0
(3)x+3y=36
例1：
(5) x+1=0






未知数的最高次数不是2次
含有两个未知数 x 和 y
这是分式方程，不是整式方程
未知数的最高次数不是2次


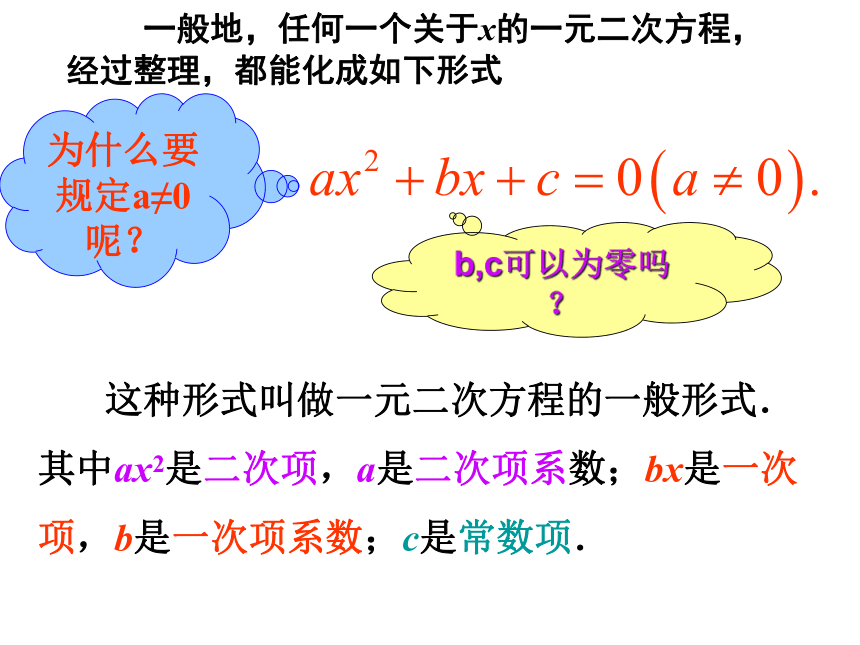
　　这种形式叫做一元二次方程的一般形式．
其中ax2是二次项，a是二次项系数；bx是一次
项，b是一次项系数；c是常数项．
　　一般地，任何一个关于x的一元二次方程，经过整理，都能化成如下形式
为什么要规定a≠0呢？
b,c可以为零吗？
一元二次方程 二次项
系数 一次项
系数 常数项
4
2x2+x+4=0
2
1
-4y2+2y=0
-4
2
0
3x2-x-1=0
3
-1
-1
抢答：你能快速完成下面的的填空吗？
4x2-5=0
4
0
-5
m-3
-(1-m)
-m
(m-3)x2-(m-1)x-m=0(m≠3)
一元二次方程的各项及其系数都包括前面的符号！
3x(x-1)=5(x+2)
这个方程能直接看出各项的系数吗？我们应该怎么办？
例2:将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.
合作探究
3x2－3x=5x+10
移项，合并同类项，得一元二次方程的一般形式：
3x2-8x-10=0
其中二次项系数为3，一次项系数为－8，常数项为－10.　　　　　　　
解：去括号，得
要想正确确定方程的系数，首先要将一元二次方程化为一般形式！
将下列方程化成一元二次方程的一般形式，并说出其中的二次项系数，一次项系数及常数项：
试一试
关于x的方程(m2-9) x2+(m-3) x +5=0，
(1)当m取何值时是一元二次方程？
(2)当m取何值时是一元一次方程？
开动脑筋
m ≠±3
m = -3
由 m2-9 ≠0 →
由 m2-9 = 0 m=±3
m -3≠0 → m≠3 →
根据下面问题，列出关于x的方程，并将其化成一般形式。
有一个用篱笆围成的长方形养鸡场，鸡场的一边靠墙（如图所示）.如果篱笆全长20米，养鸡场面积为48平方米，求养鸡场的宽x.
学以致用
x
20-2x
x（20-2x）=48
见课本27页，第2题
学以致用
练一练
祝你成功！
通过这节课的学习，谈谈你掌握了什么？