新人教版高中选修3-3物理7.1-物体是由大量分子组成的(24张PPT)
文档属性
| 名称 | 新人教版高中选修3-3物理7.1-物体是由大量分子组成的(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-18 19:04:05 | ||
图片预览







文档简介
(共24张PPT)
第七章
分子动理论
7.1
物体是由大量分子构成的
一、物体是由大量分子构成的
有哪些方法可以测量一粒西米的直径
直接测量法
能否利用测量西米直径的方法测量分子的大小?
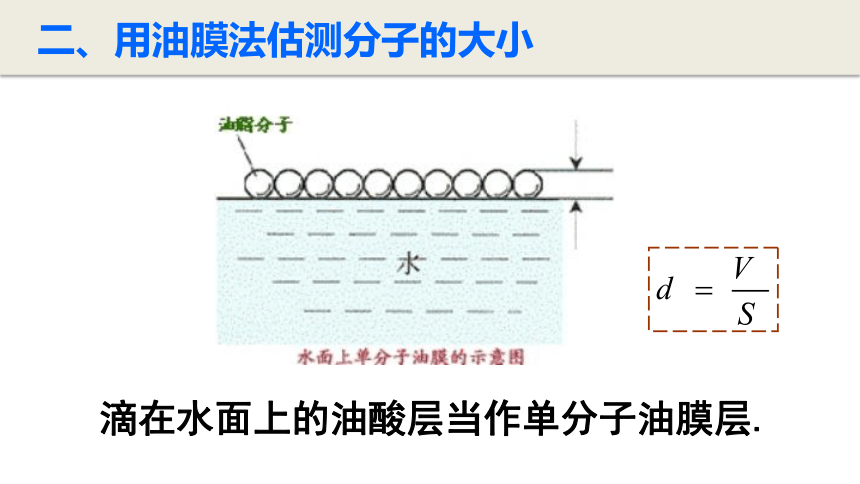
二、用油膜法估测分子的大小
球形模型:固体、液体中分子间距较小,可认为分子是一个挨着一个紧密排列的球体。
分子的结构模型
(如油酸分子等)
二、用油膜法估测分子的大小
滴在水面上的油酸层当作单分子油膜层.
实验步骤
1.测量一滴油酸分子的体积
。
二、用油膜法估测分子的大小
二、用油膜法估测分子的大小
针管滴定实验
实验步骤
1.测量一滴油酸分子的体积V
。
二、用油膜法估测分子的大小
V=V′η=ηV1/n,η为混合溶液溶度
2.测量一滴油酸分子的面积
S。
3.估测出油酸分子的直径
:
用单分子油膜法测得分子直径的数量级为
二、用油膜法估测分子的大小
注意:除一些有机物质的大分子外,一般分子的直径数量级为上面数值,以后无特别说明,我们就以上面数值作为分子直径的数量级.
二、用油膜法估测分子的大小
分子直径的数量级为
分子体积的数量级为
1mL油酸中所含的个数
分子质量的数量级为
扫描电子显微镜
三、阿伏加德罗常数及微观量的估算
1.阿伏加德罗常数:NA=6.02×1023
mol-1
它是宏观世界和微观世界之间的一座桥梁.它把
摩尔质量M、摩尔体积V、物质的质量m、物质的体积V′、物质的密度ρ等宏观量,跟单个分子的质量m0、单个分子的体积V0等微观量联系起来.
(1)一个分子的质量:m0=
.
(2)固体、液体中每个分子的体积:V0=
=
.
气体中只能求每个分子所占的空间:V0=
.
三、阿伏加德罗常数及微观量的估算
二、阿伏加德罗常数及微观量的估算
(3)质量为m的物体所含分子数:N=
.
(4)体积为V′的物体所含分子数:N=
.
物体是由大量分子组成的
用油膜法估测
分子的大小
油酸在水面上形成单分子油膜
油膜厚度:d=
分子的
大小
课堂要点小结
阿伏加德罗常数及微观量的估算
热学中
的分子
阿伏加德罗常数
分子
模型
尺度:直径的数量级10-10
m
质量:质量的数量级10-26
kg
球形模型
立方体模型
物体是由大量分子组成的
用油膜法估测
分子的大小
课堂要点小结
阿伏加德罗常数及微观量的估算
热学中
的分子
阿伏加德罗常数
大小:6.02×1023
mol-1
计
算
【例1】
在“用油膜法估测分子的大小”实验中,
104
mL油酸酒精溶液中有纯油酸6
mL.用注射
器测得1
mL上述溶液中有50滴.把1滴该溶液
滴入盛水的浅盘里,待油膜形状稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,然后把玻璃板放在坐标纸上,其形状如图1所示,坐标纸中正方形小方格的边长为20
mm.
一、用油膜法估测分子的大小
典例精析
图1
(1)油膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积是多少?
(3)根据上述数据,估测出油酸分子的直径.
一、用油膜法估测分子的大小
典例精析
解析 (1)数出在油膜轮廓范围内的格子数(面积大于半个方格的算一个,不足半个方格的舍去不算)为58个,油膜面积约为S=58×(0.02)2
m2=2.32×10-2
m2.
一、用油膜法估测分子的大小
典例精析
(1)油膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积是多少?
(3)根据上述数据,估测出油酸分子的直径.
一、用油膜法估测分子的大小
典例精析
解析 (1)数出在油膜轮廓范围内的格子数(面积大于半个方格的算一个,不足半个方格的舍去不算)为58个,油膜面积约为S=58×(0.02)2
m2=2.32×10-2
m2.
二、分子的大小
典例精析
【例2】
关于分子,下列说法中正确的是( )
A.分子看做小球是分子的简化模型,实际上,分子的形状
并不真的都是小球
B.所有分子大小的数量级都是10-10
m
C.“物体是由大量分子组成的”,其中“分子”只包含分子,
不包括原子和离子
D.分子的质量是很小的,其数量级一般为10-10
kg
A
二、分子的大小
典例精析
解析 将分子看做小球是为研究问题方便而建立的简化模型,故A选项正确.一些有机物质的分子大小的数量级超过10-10
m,故B选项错误.“物体是由大量分子组成的”,其中“分子”是分子、原子、离子的统称,故C选项错误.分子质量的数量级一般为10-26
kg,故D选项错误.
答案 A
3.已知某气体的摩尔体积为22.4
L/mol,摩尔质量为18
g/mol,阿伏加德罗常数为6.02×1023
mol-1,由以上数据可以估算出这种气体(
)
A.每个分子的质量
B.每个分子的体积
C.每个分子占据的空间
D.分子之间的平均距离
典例精析
三、阿伏加德罗常数的应用
ACD
解析 实际上气体分子之间的距离远比分子本身的线度大得多,即气体分子之间有很大空隙,故不能根据V0=
计算分子体积,这样算得的应是该气体每个分子所占据的空间,故C正确;可认为每个分子平均占据了一个小立方体空间,
即为相邻分子之间的平均距离,D正确;每个分子的质量显然可由m0=
估算,A正确.
答案 ACD
典例精析
三、阿伏加德罗常数的应用
第七章
分子动理论
7.1
物体是由大量分子构成的
一、物体是由大量分子构成的
有哪些方法可以测量一粒西米的直径
直接测量法
能否利用测量西米直径的方法测量分子的大小?
二、用油膜法估测分子的大小
球形模型:固体、液体中分子间距较小,可认为分子是一个挨着一个紧密排列的球体。
分子的结构模型
(如油酸分子等)
二、用油膜法估测分子的大小
滴在水面上的油酸层当作单分子油膜层.
实验步骤
1.测量一滴油酸分子的体积
。
二、用油膜法估测分子的大小
二、用油膜法估测分子的大小
针管滴定实验
实验步骤
1.测量一滴油酸分子的体积V
。
二、用油膜法估测分子的大小
V=V′η=ηV1/n,η为混合溶液溶度
2.测量一滴油酸分子的面积
S。
3.估测出油酸分子的直径
:
用单分子油膜法测得分子直径的数量级为
二、用油膜法估测分子的大小
注意:除一些有机物质的大分子外,一般分子的直径数量级为上面数值,以后无特别说明,我们就以上面数值作为分子直径的数量级.
二、用油膜法估测分子的大小
分子直径的数量级为
分子体积的数量级为
1mL油酸中所含的个数
分子质量的数量级为
扫描电子显微镜
三、阿伏加德罗常数及微观量的估算
1.阿伏加德罗常数:NA=6.02×1023
mol-1
它是宏观世界和微观世界之间的一座桥梁.它把
摩尔质量M、摩尔体积V、物质的质量m、物质的体积V′、物质的密度ρ等宏观量,跟单个分子的质量m0、单个分子的体积V0等微观量联系起来.
(1)一个分子的质量:m0=
.
(2)固体、液体中每个分子的体积:V0=
=
.
气体中只能求每个分子所占的空间:V0=
.
三、阿伏加德罗常数及微观量的估算
二、阿伏加德罗常数及微观量的估算
(3)质量为m的物体所含分子数:N=
.
(4)体积为V′的物体所含分子数:N=
.
物体是由大量分子组成的
用油膜法估测
分子的大小
油酸在水面上形成单分子油膜
油膜厚度:d=
分子的
大小
课堂要点小结
阿伏加德罗常数及微观量的估算
热学中
的分子
阿伏加德罗常数
分子
模型
尺度:直径的数量级10-10
m
质量:质量的数量级10-26
kg
球形模型
立方体模型
物体是由大量分子组成的
用油膜法估测
分子的大小
课堂要点小结
阿伏加德罗常数及微观量的估算
热学中
的分子
阿伏加德罗常数
大小:6.02×1023
mol-1
计
算
【例1】
在“用油膜法估测分子的大小”实验中,
104
mL油酸酒精溶液中有纯油酸6
mL.用注射
器测得1
mL上述溶液中有50滴.把1滴该溶液
滴入盛水的浅盘里,待油膜形状稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,然后把玻璃板放在坐标纸上,其形状如图1所示,坐标纸中正方形小方格的边长为20
mm.
一、用油膜法估测分子的大小
典例精析
图1
(1)油膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积是多少?
(3)根据上述数据,估测出油酸分子的直径.
一、用油膜法估测分子的大小
典例精析
解析 (1)数出在油膜轮廓范围内的格子数(面积大于半个方格的算一个,不足半个方格的舍去不算)为58个,油膜面积约为S=58×(0.02)2
m2=2.32×10-2
m2.
一、用油膜法估测分子的大小
典例精析
(1)油膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积是多少?
(3)根据上述数据,估测出油酸分子的直径.
一、用油膜法估测分子的大小
典例精析
解析 (1)数出在油膜轮廓范围内的格子数(面积大于半个方格的算一个,不足半个方格的舍去不算)为58个,油膜面积约为S=58×(0.02)2
m2=2.32×10-2
m2.
二、分子的大小
典例精析
【例2】
关于分子,下列说法中正确的是( )
A.分子看做小球是分子的简化模型,实际上,分子的形状
并不真的都是小球
B.所有分子大小的数量级都是10-10
m
C.“物体是由大量分子组成的”,其中“分子”只包含分子,
不包括原子和离子
D.分子的质量是很小的,其数量级一般为10-10
kg
A
二、分子的大小
典例精析
解析 将分子看做小球是为研究问题方便而建立的简化模型,故A选项正确.一些有机物质的分子大小的数量级超过10-10
m,故B选项错误.“物体是由大量分子组成的”,其中“分子”是分子、原子、离子的统称,故C选项错误.分子质量的数量级一般为10-26
kg,故D选项错误.
答案 A
3.已知某气体的摩尔体积为22.4
L/mol,摩尔质量为18
g/mol,阿伏加德罗常数为6.02×1023
mol-1,由以上数据可以估算出这种气体(
)
A.每个分子的质量
B.每个分子的体积
C.每个分子占据的空间
D.分子之间的平均距离
典例精析
三、阿伏加德罗常数的应用
ACD
解析 实际上气体分子之间的距离远比分子本身的线度大得多,即气体分子之间有很大空隙,故不能根据V0=
计算分子体积,这样算得的应是该气体每个分子所占据的空间,故C正确;可认为每个分子平均占据了一个小立方体空间,
即为相邻分子之间的平均距离,D正确;每个分子的质量显然可由m0=
估算,A正确.
答案 ACD
典例精析
三、阿伏加德罗常数的应用
