1.11探索勾股定理

内 容 §1.1探索勾股定理（１） 使用时间 201年9月　日
主备人 李磊 参与人 邱增胜　杨银龙 刘志　　赵剑波 审核
学习目标：1、经历探索数格子的方法发现勾股定理，并利用拼图的方法论证勾股定理的存在。
2、结合具体的情境，理解和掌握“直角三角形两条直角边的平方和等于斜边的平方”。
3、探索和实际操作掌握勾股定理在实际生活中的应用。
教学重点：是对勾股定理的理解，以及运用勾股定理去解决一些相关的实际问题。
教学难点：是勾股定理的探索和验证过程中，进一步体会数形结合的思想，学习中应注意加辅助线的方法。
一、学前准备
一棵大树在一次强烈台风中于离地面5m处折断倒下，树顶落在离树根12m处. 大树在折断之前高多少
　　　　　　　　　　　　　　　　　
二、探究活动
1.自主探究 解决问题
动手测量找直角三角形三边关系
活动目的：通过测量寻找直角三角形三边之间的关系
活动工具：直尺、笔、作业纸
活动程序：
（1）四人为一个小组，每个人在自己的纸上画1-2个不同的直角三角形
（2）组内交换纸片，用直尺测量同伴所画直角三角形的各边长，完善下面的表格
（3）观察并大胆猜测结果中三角形的三边长的平方有什么关系？
直角边a a的平方 直角边b B的平方 斜边c C的平方 三边关系
第一个
第二个
第三个
第四个
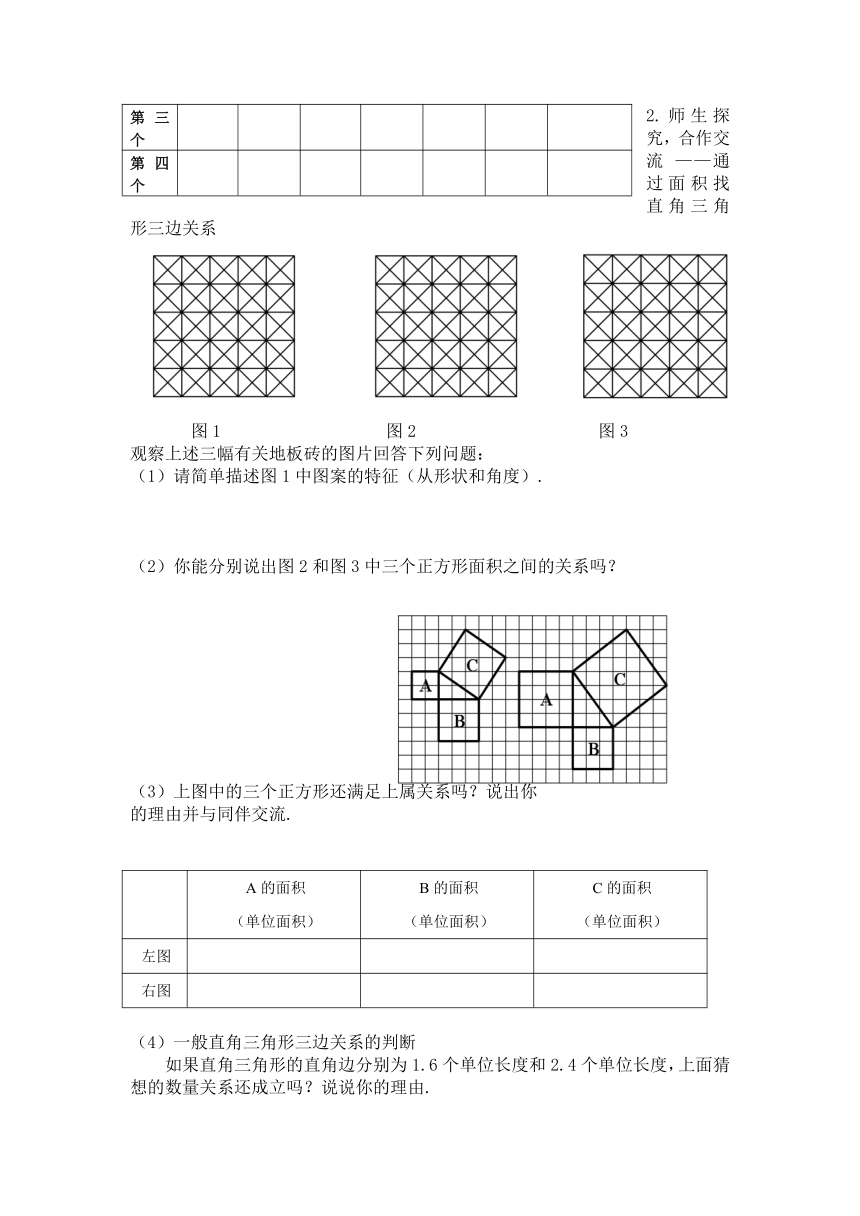
2.师生探究，合作交流 ——通过面积找直角三角形三边关系
图1 图2 图3
观察上述三幅有关地板砖的图片回答下列问题：
（1）请简单描述图1中图案的特征（从形状和角度）.
（2）你能分别说出图2和图3中三个正方形面积之间的关系吗？
（3）上图中的三个正方形还满足上属关系吗？说出你
的理由并与同伴交流.
A的面积（单位面积） B的面积（单位面积） C的面积（单位面积）
左图
右图
（4）一般直角三角形三边关系的判断
如果直角三角形的直角边分别为1.6个单位长度和2.4个单位长度，上面猜想的数量关系还成立吗？说说你的理由.
（5）归纳总结：通过上面的活动，同学们一定发现，直角三角形三边长度之间的关系是：
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
这就是著名的“勾股定理”。
公式：如果直角三角形的两直角边为a、b，斜边为c。那么
我国古代称直角三角形的较短的直角边为勾，较长的直角边为股，斜边为弦，这就是勾股定理的由来。
注意：勾股定理存在于（ ）三角形中，不是（ ）三角形就不能使用勾股定理。
三、我的课堂我做主
１.介绍勾、股、弦
（ 　 ）
（ 　 ）
（ 　 ）
2.如图，你能计算出下列直角三角形中未知边的长吗？
四、巩固练习
1.已知在Rt△ABC中，∠C=90°。
①若a=3，b=4，则c=________；
②若a=40，b=9，则c=________；
③若a=6，c=10，则b=_______；
④若c=25，b=15，则a=________。
2.小明.小红在同一位置，小明向北走了6m，小红向东走了8m，这时两人相距 m.
3.等腰△ABC中，AB=AC=17cm，BC=16cm，则△ABC的面积是
五、学习心得
通过本节课的学习你有哪些收获？
六、应用拓展　　　　　　　　　　　　　　　　
四边形ABCD中，∠BAD =，∠DBC =，AD = 3，AB = 4，BC = 12，求CD