四年级上册数学试题-3.1直线射线线段和角 人教版 无答案
文档属性
| 名称 | 四年级上册数学试题-3.1直线射线线段和角 人教版 无答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 00:00:00 | ||
图片预览

文档简介
角提高训练
考点?方法?破译
1.进一步认识角,会比较角的大小,会计算角度的和差,认识度、分、秒,会进行简单的换算.
2.了解角平分线及其性质,了角余角、补角,知道等角的余角相等,等角的补角相等.
经典?考题?赏析
例1:如图AOE是直线,图中小于平角的角共有( )
A.7个 B.9个 C.8个 D.10个
【变式题组】
1.在下图中一共有几个角?它们应如何表示.
2.下列语句正确的是( )
A.从同一点引出的两条射线组成的图形叫做角 B.两条直线相交组成的图形叫做角
C.从同一点引出的两条线段组成的图形叫做角 D.两条线段相交组成的图形叫做角
3.关于平角和周角的说法正确的是( )
A.平角是一条直线 B.周角是一条射线
C.反向延长射线OA,就是成一个平角 D.两个锐角的和不一定小于平角
例:38.33°可化为( )
A.38°30′3〃 B.38°33' C.38°30′30″〃 D.38°19′48″〃
1.把下列各角化成用度表示的角:
⑴15°24′36″〃 ⑵36°59′96″〃 ⑶50°65′60″〃
2.⑴3.76°= 度 分 秒⑵3.76°= 分 秒
⑶钟表在8:30时,分针与时针的夹角为 度.
3.计算:
⑴23°45′36+66°14′24″; ⑵180°-98°24′30″;〃⑶15°50′42″×3; ⑷88°14′48″÷4
例:若∠α的余角与∠α的补角的和是平角则∠α= .
【变式题组】
1.如图所示,那么∠2与之间的关系是( )
A.互补 B.互余 C.和为45° D.和为22.5°
2.55°角的余角是( )
A.55° B.45° C.35° D.125°
4.若∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°-∠β;②∠α-90°;③④( )
A.4个 B.3个 C.2个 D.1个
例4:如图,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,则∠AOC= .
【变式题组】
1.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD等于( )
A.20° B.40° C.50° D.80°
2.如图直线a,b相交于点O,若∠1=40°,则∠2等于( )
A.50° B.60° C.140° D.160°
3.一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为( )
A.45° B.60° C.75° D.80°
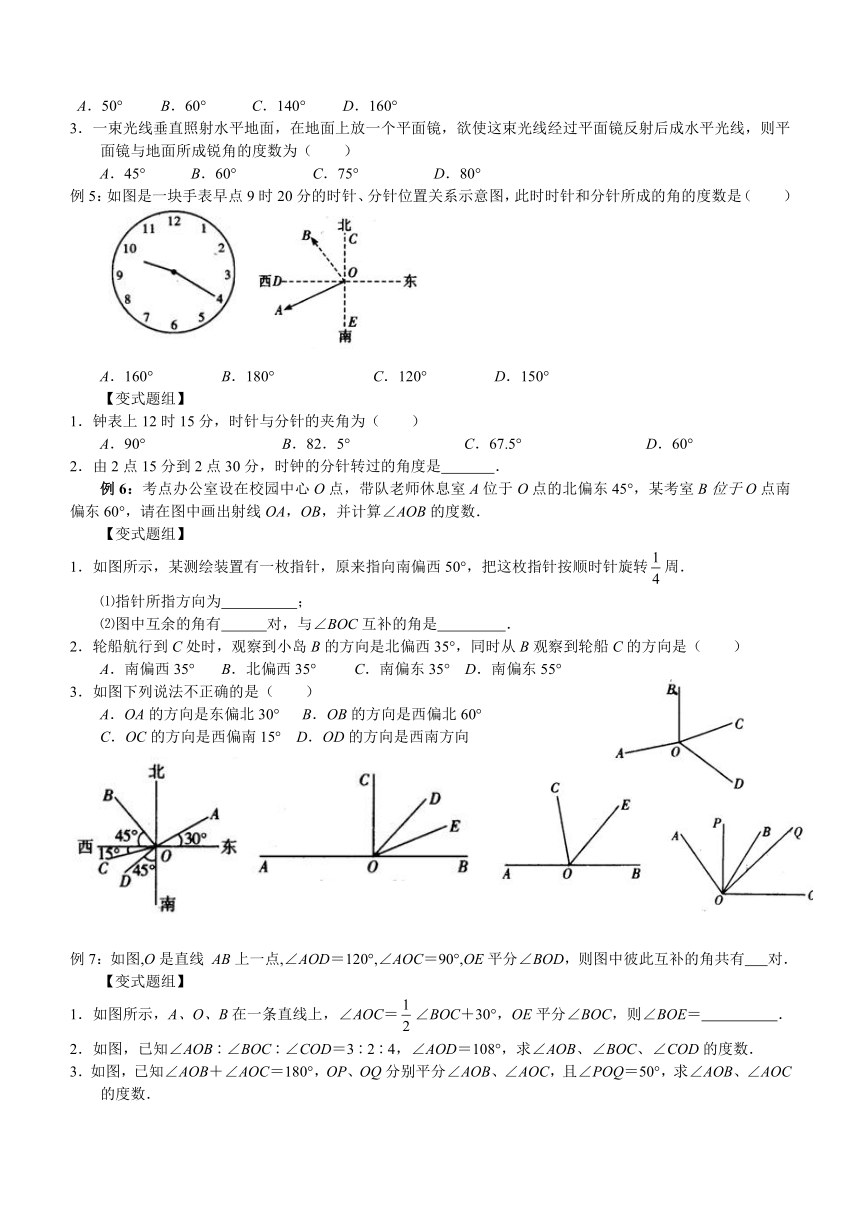
例5:如图是一块手表早点9时20分的时针、分针位置关系示意图,此时时针和分针所成的角的度数是( )
A.160° B.180° C.120° D.150°
【变式题组】
1.钟表上12时15分,时针与分针的夹角为( )
A.90° B.82.5° C.67.5° D.60°
2.由2点15分到2点30分,时钟的分针转过的角度是 .
例6:考点办公室设在校园中心O点,带队老师休息室A位于O点的北偏东45°,某考室B位于O点南偏东60°,请在图中画出射线OA,OB,并计算∠AOB的度数.
【变式题组】
1.如图所示,某测绘装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针旋转周.
⑴指针所指方向为 ;
⑵图中互余的角有 对,与∠BOC互补的角是 .
2.轮船航行到C处时,观察到小岛B的方向是北偏西35°,同时从B观察到轮船C的方向是( )
A.南偏西35° B.北偏西35° C.南偏东35° D.南偏东55°
3.如图下列说法不正确的是( )
A.OA的方向是东偏北30° B.OB的方向是西偏北60°
C.OC的方向是西偏南15° D.OD的方向是西南方向
例7:如图,O是直线 AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中彼此互补的角共有 对.
【变式题组】
1.如图所示,A、O、B在一条直线上,∠AOC=∠BOC+30°,OE平分∠BOC,则∠BOE= .
2.如图,已知∠AOB∶∠BOC∶∠COD=3∶2∶4,∠AOD=108°,求∠AOB、∠BOC、∠COD的度数.
3.如图,已知∠AOB+∠AOC=180°,OP、OQ分别平分∠AOB、∠AOC,且∠POQ=50°,求∠AOB、∠AOC的度数.
演练巩固 反馈提高:
1.已知∠α=35°,则∠α的余角是( )
A.55° B.45° C.145° D.135°
2.如图直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于( )
A.56° B.46° C.45° D.44°
3.把一张长方形的纸片按图的方位折叠,EM、FM为折痕,折叠后的C点落在MB'的延长线上,则∠EMF的度数是( )
A.85° B.90° C.95° D.100°
4.书店、学校、食堂在同一个平面上,分别用A、B、C表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC应是( )
A.65° B.35° C.165° D.135°
5.如果∠α=3∠β,∠α=2∠θ,则必有( )
A. B. C. D.
6.某校初一年级在下午3:00开展“阳光体育”活动,下午3:00这一时刻,时针上分针与时针所夹角等于 °.
7.已知∠AOB=30°,又自∠AOB的顶点O引射线OC,若∠AOC:∠AOB =4:3,那么∠BOC等于( )
A.10° B.40° C.45° D.70°或10°
8.已知∠AOB=120°,OC在它的内部,且把∠AOB分成1:3,那么∠AOC的度数是( )
A.40° B.40°或80° C.30° D.30°或90°
9.一个角的补角的是6°,则这个角是( )
A.68° B.78° C.88° D.98°
10.如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α余角相等的是( )
A.∠COD B.∠COE C.∠DOA D.∠COA
10.4点钟后,时针与分针第二次成90°,共经过( )分钟(答案四舍五入到整数).
A.60 B.30 C.40 D.33
11.如图OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线,则下列各式中成立的是( )
A.∠AOP >∠MON B.∠AOP =∠MON
C.∠AOP <∠MON D.以上情况都有可能
12.如图,∠AOC是直角,∠COD=21.5°,且OB、OD分别是∠AOC、∠BOE的平分线,则∠AOE等于( )
A.111.5° B.138° C.134.5° D.178°
13.下列说法不正确的是( )
A.角的大小与角的边画出部分的长短无关
B.角的大小与它们的度数的大小是一至的
C.角的平分线是一条线段
D.角的和、差、倍、分的度数等于它们度数的和、差、倍、分
14.和艘轮船由A地向南偏西45°的方向行驶40海里到达B地,再由B地向北偏西15°方向行驶40海里到达C地,则A、C相距( )海里.
A.30 B.40 C.50 D.60
15.∠A的补角是125°12',则它的余角是( )
A.54°18' B.35°12' C.35°48' D.54°48'
16.如果一个角等于它的余角的2倍,那么这个角等于它补角的( )
A.2倍 B.倍 C.5倍 D.倍
17.一个角的补角与这个角的余角的度数之比为3:1,则这个角是 度.
18.α、β、γ中有两个锐角和一个钝角,其数值已经给出,在计算(α+β+γ)的值时,有三位同学分别算出了23°、24°、25°这三个不同的结果,其中确有一个是正确答案,则α+β+γ= .
19.已知∠AOB=50°,∠BOD=3∠AOB,OC平分∠AOB,OM平分∠AOD,求∠MOC的度数.
20. ⑴如图所示,已知∠AOB是直角,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;⑵如果⑴中∠AOB=α,其他条件不变,求∠MON的度数;
⑶你从⑴⑵的结果中,能发现什么规律?
21.如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
⑴若∠AOD=70°,∠MON=50°,求∠BOC的大小;
⑵若∠AOD=α,∠MON=β,求∠BOC的大小.(用字母α、β的式子表示)
22.如图所示,已知∠AOE=100°,∠DOF=80°,OE平分∠DOC,OF平分∠AOC,求∠EOF的度数.
23.如图所示,O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线.
⑴求∠DOE的度数;
⑵若只将射线OC的位置改变,其他条件不变,那么∠DOE的度数会改变吗?
24.如图,根据图回答下列问题:
⑴∠AOC是哪两个角的和;
⑵∠AOB是哪两个角的差.
25.如图,∠1=∠2=∠3=∠4,根据图形回答问题:
⑴图中哪些角是∠2的2倍;
⑵图中哪些角是∠3的3倍;
⑶图中哪些角是∠AOD的倍;
⑷射线OC是哪个角的三等分线.
26.如图直线AB与CD相交于点O ,那么∠1=∠2吗?试说明理由.
考点?方法?破译
1.进一步认识角,会比较角的大小,会计算角度的和差,认识度、分、秒,会进行简单的换算.
2.了解角平分线及其性质,了角余角、补角,知道等角的余角相等,等角的补角相等.
经典?考题?赏析
例1:如图AOE是直线,图中小于平角的角共有( )
A.7个 B.9个 C.8个 D.10个
【变式题组】
1.在下图中一共有几个角?它们应如何表示.
2.下列语句正确的是( )
A.从同一点引出的两条射线组成的图形叫做角 B.两条直线相交组成的图形叫做角
C.从同一点引出的两条线段组成的图形叫做角 D.两条线段相交组成的图形叫做角
3.关于平角和周角的说法正确的是( )
A.平角是一条直线 B.周角是一条射线
C.反向延长射线OA,就是成一个平角 D.两个锐角的和不一定小于平角
例:38.33°可化为( )
A.38°30′3〃 B.38°33' C.38°30′30″〃 D.38°19′48″〃
1.把下列各角化成用度表示的角:
⑴15°24′36″〃 ⑵36°59′96″〃 ⑶50°65′60″〃
2.⑴3.76°= 度 分 秒⑵3.76°= 分 秒
⑶钟表在8:30时,分针与时针的夹角为 度.
3.计算:
⑴23°45′36+66°14′24″; ⑵180°-98°24′30″;〃⑶15°50′42″×3; ⑷88°14′48″÷4
例:若∠α的余角与∠α的补角的和是平角则∠α= .
【变式题组】
1.如图所示,那么∠2与之间的关系是( )
A.互补 B.互余 C.和为45° D.和为22.5°
2.55°角的余角是( )
A.55° B.45° C.35° D.125°
4.若∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°-∠β;②∠α-90°;③④( )
A.4个 B.3个 C.2个 D.1个
例4:如图,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,则∠AOC= .
【变式题组】
1.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD等于( )
A.20° B.40° C.50° D.80°
2.如图直线a,b相交于点O,若∠1=40°,则∠2等于( )
A.50° B.60° C.140° D.160°
3.一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为( )
A.45° B.60° C.75° D.80°
例5:如图是一块手表早点9时20分的时针、分针位置关系示意图,此时时针和分针所成的角的度数是( )
A.160° B.180° C.120° D.150°
【变式题组】
1.钟表上12时15分,时针与分针的夹角为( )
A.90° B.82.5° C.67.5° D.60°
2.由2点15分到2点30分,时钟的分针转过的角度是 .
例6:考点办公室设在校园中心O点,带队老师休息室A位于O点的北偏东45°,某考室B位于O点南偏东60°,请在图中画出射线OA,OB,并计算∠AOB的度数.
【变式题组】
1.如图所示,某测绘装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针旋转周.
⑴指针所指方向为 ;
⑵图中互余的角有 对,与∠BOC互补的角是 .
2.轮船航行到C处时,观察到小岛B的方向是北偏西35°,同时从B观察到轮船C的方向是( )
A.南偏西35° B.北偏西35° C.南偏东35° D.南偏东55°
3.如图下列说法不正确的是( )
A.OA的方向是东偏北30° B.OB的方向是西偏北60°
C.OC的方向是西偏南15° D.OD的方向是西南方向
例7:如图,O是直线 AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中彼此互补的角共有 对.
【变式题组】
1.如图所示,A、O、B在一条直线上,∠AOC=∠BOC+30°,OE平分∠BOC,则∠BOE= .
2.如图,已知∠AOB∶∠BOC∶∠COD=3∶2∶4,∠AOD=108°,求∠AOB、∠BOC、∠COD的度数.
3.如图,已知∠AOB+∠AOC=180°,OP、OQ分别平分∠AOB、∠AOC,且∠POQ=50°,求∠AOB、∠AOC的度数.
演练巩固 反馈提高:
1.已知∠α=35°,则∠α的余角是( )
A.55° B.45° C.145° D.135°
2.如图直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于( )
A.56° B.46° C.45° D.44°
3.把一张长方形的纸片按图的方位折叠,EM、FM为折痕,折叠后的C点落在MB'的延长线上,则∠EMF的度数是( )
A.85° B.90° C.95° D.100°
4.书店、学校、食堂在同一个平面上,分别用A、B、C表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC应是( )
A.65° B.35° C.165° D.135°
5.如果∠α=3∠β,∠α=2∠θ,则必有( )
A. B. C. D.
6.某校初一年级在下午3:00开展“阳光体育”活动,下午3:00这一时刻,时针上分针与时针所夹角等于 °.
7.已知∠AOB=30°,又自∠AOB的顶点O引射线OC,若∠AOC:∠AOB =4:3,那么∠BOC等于( )
A.10° B.40° C.45° D.70°或10°
8.已知∠AOB=120°,OC在它的内部,且把∠AOB分成1:3,那么∠AOC的度数是( )
A.40° B.40°或80° C.30° D.30°或90°
9.一个角的补角的是6°,则这个角是( )
A.68° B.78° C.88° D.98°
10.如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α余角相等的是( )
A.∠COD B.∠COE C.∠DOA D.∠COA
10.4点钟后,时针与分针第二次成90°,共经过( )分钟(答案四舍五入到整数).
A.60 B.30 C.40 D.33
11.如图OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线,则下列各式中成立的是( )
A.∠AOP >∠MON B.∠AOP =∠MON
C.∠AOP <∠MON D.以上情况都有可能
12.如图,∠AOC是直角,∠COD=21.5°,且OB、OD分别是∠AOC、∠BOE的平分线,则∠AOE等于( )
A.111.5° B.138° C.134.5° D.178°
13.下列说法不正确的是( )
A.角的大小与角的边画出部分的长短无关
B.角的大小与它们的度数的大小是一至的
C.角的平分线是一条线段
D.角的和、差、倍、分的度数等于它们度数的和、差、倍、分
14.和艘轮船由A地向南偏西45°的方向行驶40海里到达B地,再由B地向北偏西15°方向行驶40海里到达C地,则A、C相距( )海里.
A.30 B.40 C.50 D.60
15.∠A的补角是125°12',则它的余角是( )
A.54°18' B.35°12' C.35°48' D.54°48'
16.如果一个角等于它的余角的2倍,那么这个角等于它补角的( )
A.2倍 B.倍 C.5倍 D.倍
17.一个角的补角与这个角的余角的度数之比为3:1,则这个角是 度.
18.α、β、γ中有两个锐角和一个钝角,其数值已经给出,在计算(α+β+γ)的值时,有三位同学分别算出了23°、24°、25°这三个不同的结果,其中确有一个是正确答案,则α+β+γ= .
19.已知∠AOB=50°,∠BOD=3∠AOB,OC平分∠AOB,OM平分∠AOD,求∠MOC的度数.
20. ⑴如图所示,已知∠AOB是直角,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;⑵如果⑴中∠AOB=α,其他条件不变,求∠MON的度数;
⑶你从⑴⑵的结果中,能发现什么规律?
21.如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
⑴若∠AOD=70°,∠MON=50°,求∠BOC的大小;
⑵若∠AOD=α,∠MON=β,求∠BOC的大小.(用字母α、β的式子表示)
22.如图所示,已知∠AOE=100°,∠DOF=80°,OE平分∠DOC,OF平分∠AOC,求∠EOF的度数.
23.如图所示,O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线.
⑴求∠DOE的度数;
⑵若只将射线OC的位置改变,其他条件不变,那么∠DOE的度数会改变吗?
24.如图,根据图回答下列问题:
⑴∠AOC是哪两个角的和;
⑵∠AOB是哪两个角的差.
25.如图,∠1=∠2=∠3=∠4,根据图形回答问题:
⑴图中哪些角是∠2的2倍;
⑵图中哪些角是∠3的3倍;
⑶图中哪些角是∠AOD的倍;
⑷射线OC是哪个角的三等分线.
26.如图直线AB与CD相交于点O ,那么∠1=∠2吗?试说明理由.
